材料力学・構造力学 モーメント荷重を作用させた時のたわみの式 片持ち梁

モーメント荷重を作用させたときのたわみの式ってどうなるの？

苦手君

本日は片持ち梁にモーメント荷重が作用したときのたわみの式について解説します。

モーメント荷重が作用した時の曲げモーメント図（BMD）は過去の記事で導出していますので、そちらを参考にしていただければと思います。

モデル

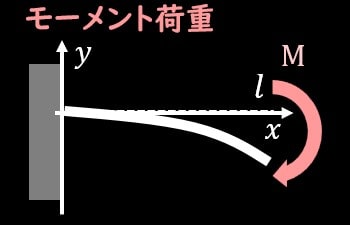
片持ち梁にモーメント荷重が作用している場合のモデルは上図のようになります。

座標軸は固定端側を原点として今回は考えます。

曲げモーメントの式

曲げモーメントの式は下記のように表すことができます。

$$\frac{d^2y}{dx^2}=\frac{M}{EI}$$

\(M\)は曲げモーメント、\(E\)はヤング率、\(I\)は断面2次モーメントです。

片持ち梁にモーメント荷重\(M_0\)が作用している時の曲げモーメントは前回の記事で解説しております。

$$M=M_0$$

ですので、これを曲げモーメントの式に入れましょう。

$$\frac{d^2y}{dx^2}=\frac{M_0}{EI}$$

あとはこの微分方程式を解くことで、たわみの式を求めることができます。

この微分方程式は直接積分系とよばれる微分方程式なので、両辺を積分していくことで求めることができます。

微分方程式を解く

両辺を積分する

それでは積分をしていきましょう。

まず両辺を一回ずつ積分すると、

$$\frac{dy}{dx}=\frac{M_0}{EI}x+C_1$$

このようになります。\(C_1\)は積分定数です。

さらにもう一回積分すると、

$$y=\frac{M_0}{2EI}x^2+C_1x+C_2$$

\(C_2\)は積分定数です。

積分定数を求める

次に積分定数を求める必要がありますので、境界条件を使って積分定数を求めます。

片持ち梁の場合、固定端における変位\(y\)とたわみ角θがゼロとなります。

たわみ角θは

$$θ=\frac{dy}{dx}$$

ですので、\(x＝0\)のとき\(θ＝0\)となるため、

$$C_1=0$$

となります。同様に、\(y(0)=0\)より、

$$C_2=0$$

となりますね。

よって、たわみの式は

$$y=\frac{M_0}{2EI}x^2$$

となって、最大たわみ量δは\(x=l\)のときなので、

$$δ=\frac{M_0l^2}{EI}$$

となります。

まとめ

モーメント荷重が片持ち梁に作用した時のたわみの式を導出しました。

モーメント荷重の場合は計算も非常に簡単ですので、しっかりと求め方の流れを理解しておきましょう。

初心者向けの教科書・参考書もこちらで紹介しておりますので、参考にしていただければと思います。

材料力学の記事一覧はこちら。