材料力学 構造力学 両端固定梁のたわみの式を導出する （不静定問題の解き方）

本記事では両端固定梁のたわみの式を導出します。

最終的にたわみの式の計算までいかないと、BMD（曲げモーメント図）を描くことができませんので、BMDとたわみの式の両方を計算で求めていきます。

動画でも解説しておりますので、そちらも是非参考にしていただければと思います。

モデル

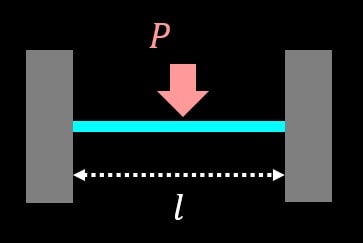
両端固定梁は、梁の両端を固定端でがっちりと固定した状態の梁です。

今回は真ん中に集中荷重\(P\)が作用している場合を考えます。

たわみの式を導出するまでの流れ

まずはたわみの式を導出するまでの全体の流れを説明します。

流れ自体は片持ち梁や単純梁と同じです。

まずはBMDを下の流れで求めます。

ここまでで、曲げモーメントが求まることになりますので、曲げモーメントの式に代入して、微分方程式を解いてたわみの式を導出します。

ここでポイントになるのは、片持ち梁や単純梁の場合と異なるのは、STEP2で反力、反モーメントが未知数で現れるのですが、

これらをSTEP2の時点で求めることができないことです。

これらの未知数（反力、反モーメント）は、後のたわみの式を導出する際に出てくる積分定数と合わせて、境界条件を用いることで求めることになります。

ここまでの説明は、ふ〜ん、と思っていただければ大丈夫です。

それではまずは曲げモーメント図を求める5STEPをやっていきましょう。

座標軸をとる

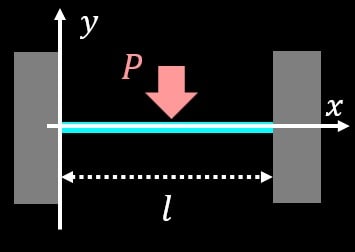
基本的に座標軸はどのようにとってもOKです。

今回は上記のように座標軸を取ります。(右側の固定端を原点にとってもOKです）

つり合いの条件を考える

それでは梁全体のつり合いの条件を考えましょう。

x方向のつり合いについては、x方向に力が作用していませんので、考える必要がなく、y方向の力のつり合いをまずは考えましょう。

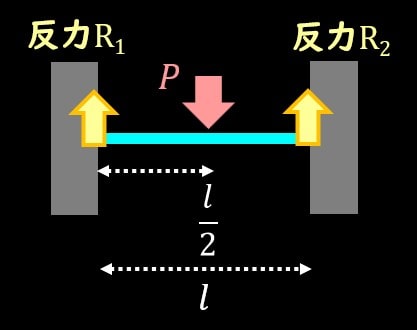
\(y\)方向の力は荷重\(P\)が作用していますね。

このままだと梁はどこかに飛んでいってしまうので、固定端から反力\(R_1\), \(R_2\)を受けます。

よって\(y\)方向のつり合いの式は

$$P=R_1+R_2$$

となります。

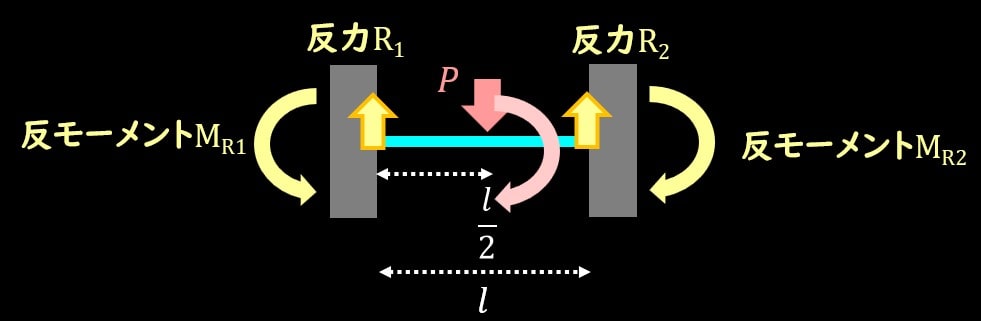
次にモーメントのつり合いですが、原点からみたモーメントのつり合いの式を考えましょう。

荷重\(P\)が長さ\(l\)の梁の中央に作用していますので、モーメントは

$$M_P=\frac{Pl}{2}$$

となります。

これに加えて、固定端から受けるモーメントを考える必要があります。

ここで注意するポイントしては、 固定端に発生した反力によるモーメントと、反モーメントは別と考えてください。

図の\(R_2l\)と\(M_{R2}\)ですね。

反モーメントは固定端であるがゆえに、強制的に発生するモーメントだと捉えてください。

さらに、原点周りの反モーメント\(M_{R1}\)もモーメントのつり合いの式では必要になります。（距離ゼロだからゼロ、という風にはなりませんので注意です！）

これらとのモーメントのつり合いを考えると、

$$M_{R1}+M_P-R_2l-M_{R2}=0$$

ここで、荷重が梁の中央に作用している場合、対称性から\(M_{R1}=M_{R2}\)となり、

$$M_P-R_2l=0$$

となります。

\(M_P\)を荷重を使って書き直すと、

$$\frac{Pl}{2}-R_2l=0$$

第１項を移項して、両辺を\(l\)で割ると、

$$R_2=\frac{P}{2}$$

\(P=R_1+R_2\)であるから、

$$R_1=\frac{P}{2}$$

このような形で、2つの反力\(R_1\)、\(R_2\)は求まりました。

しかし、反モーメントの\(M_{R1}\)と\(M_{R2}\)は未知数のままで、求めることができません。

さて、どうするか？

どうもしません、このまま進みましょう。

切断してせん断力を書く

次のステップ、切断してせん断力を描くに移ります。

適当なところで切断して、切断した部分で力のつり合いが成立するように、せん断力を設定する、という流れになります。

今回、荷重が梁中央に作用していますので、荷重の左側で切断した場合と、右側で切断した場合とで場合わけする必要があります。

それではまず荷重の左側で切断した場合を考えましょう。

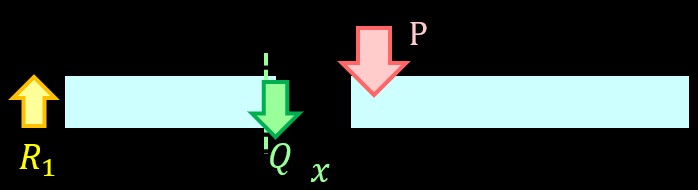
左側で切断した場合、切断した部分に作用している力は反力\(R_1\)だけですね。

よって、力のつり合いを考えると、切断面には反力と逆向きに\(R_1\)の大きさのせん断力\(Q_1\)が発生します。

\(R_1=\frac{P}{2}\)なので、\(Q_1\)は下記のようになります。

$$Q_1=\frac{P}{2}$$

せん断力は棒の右側の面に作用する場合、下向きが正ですので、符号はプラスとなります。

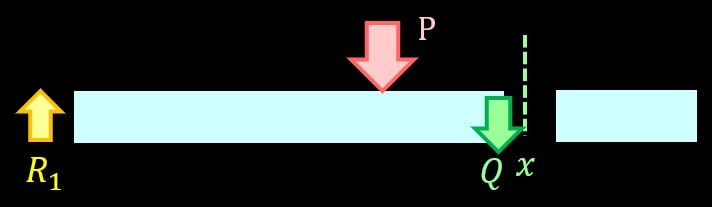
それでは次に、荷重の右側で切断した時のせん断力を考えましょう。

切断した部分に作用している力は、左側の固定端から受ける反力\(R_1\)と、荷重Pの二つですね。

これらとつり合うようにせん断力\(Q_2\)が発生しますので、下向きを正とすると、

$$Q_2=-P+R_1=-P+\frac{P}{2}=-\frac{P}{2}$$

となります。

以上からせん断力図（SFD）を描くと下図のようになります。

せん断力によるモーメントを描く

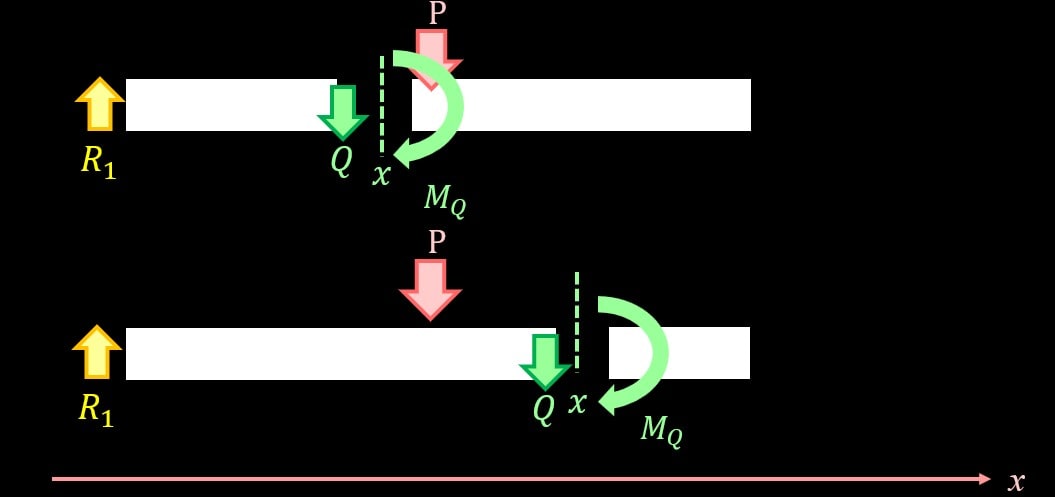
切断面にせん断力が発生するということは、せん断力によるモーメントも発生するということになります。

モーメントを考えるにあたって、支点を設定する必要がありますので、今回は支点を左側の固定端部分とします。

左側の固定端からの距離\(x\）における、せん断力によるモーメントは

$$M_{Q1}=Q_1x$$

$$M_{Q2}=Q_2x$$

ですね。それぞれ梁中央より左側のモーメントが\(M_{Q1}\)、梁中央より右側のモーメントが$M_{Q2}$です。

これらのモーメントを使って、最後のステップ、モーメントのつり合いを考えていきましょう。

切断した部分のモーメントのつり合い

さて、モーメントのつり合いを考えるわけですが、せん断力の時と同様、荷重の左側と右側で場合わけが必要となります。

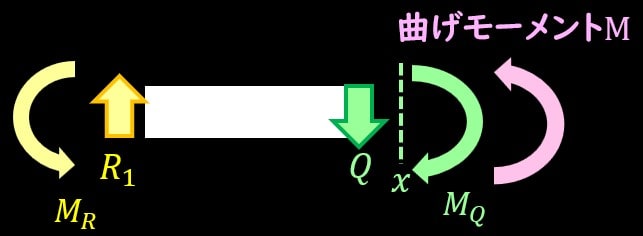
それでは荷重の左側を考えてみます。

作用しているモーメントは、固定端で発生してる反モーメント\(M_{R1}\)、せん断力によるモーメント\(M_{Q1}\)の2つですね。

これらとつり合うように曲げモーメントMを切断面に作用させてあげる必要がありますので、モーメントのつり合いの式を考えましょう。

$$M_1-M_{Q1}=M_{R1}$$

移項して\(M_{Q1}=Q_1x=\frac{Px}{2}\)を代入し、整理しておくと、

$$M_1=\frac{Px}{2}+M_{R1}$$

ここで、\(M_{R1}\)は未知数なので、このままにしておきます。

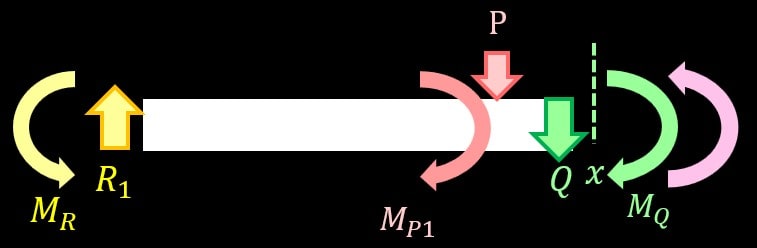
次に荷重の右側の曲げモーメントを考えましょう。

荷重より右側の場合、作用しているモーメントは、下の3つですね。

• 反モーメント \(M_{R1}\)
• 荷重によるモーメント\(M_{P1}=\frac{Pl}{2}\)
• せん断力によるモーメント \(M_{Q2}=-\frac{Px}{2}\)

これらとつり合うようにモーメントのつり合いの式を考えると、

$$M-\frac{Px}{2}-\frac{Pl}{2}=M_{R1}$$

式を整理すると、

$$M_2=\frac{P}{2}(l-x)+M_{R1}$$

となります。

ここでも未知数の\(M_{R1}\)がありますので、このままにしておきます。

たわみの式を導出する

両端固定梁のような不静定問題では、 未知数を残したまま、たわみの式を導出しに行きます。

たわみの式を導出する過程で、積分定数を求める際に未知数も求めることができますので、安心して読み進めてください。

曲げモーメントの式は下記のように表すことができます。

$$\frac{d^2y}{dx^2}=\frac{M}{EI}$$

\(E\)はヤング率、\(I\)は断面2次モーメントです。

この式の解説については、過去の記事を参考にしていただければと思います。

この式の両辺を積分することで、たわみの式を導出してことになります。

ということで、両辺を積分しましょう。

$$\frac{dy}{dx}=\int\frac{M}{EI}dx$$

曲げモーメント\(M\)は先ほど求めた通り、荷重より左側では、

$$M_1=\frac{Px}{2}+M_{R1}$$

荷重より右側では、

$$M_2=\frac{P}{2}(l-x)+M_{R1}$$

ですので、まずは\(M_1\)代入して計算しましょう。

$$\frac{dy_1}{dx}=\int\frac{1}{EI}\left(\frac{Px}{2}+M_{R1}\right)dx$$

$$=\frac{1}{EI}\left(\frac{Px^2}{4}+M_{R1}x\right)+C_1$$

この式をもう一回積分するとたわみ量yの式が導出できて、

$$y_1=\int\frac{1}{EI}\left[\frac{1}{EI}\left(\frac{Px^2}{4}+M_{R1}x\right)+C_1\right]dx$$

積分を実行すると、

$$y_1=\frac{1}{EI}\left(\frac{Px^3}{12}+\frac{M_{R1}x^2}{2}\right)+C_1x+C_2$$

となります。

次に荷重の右側について考えます。

曲げモーメントは\(M_2\)となります。

$$\frac{dy_2}{dx^2}=\frac{1}{EI}\left(\frac{P}{2}(l-x)-M_{R1}\right)$$

この式を1回積分すると、

$$\frac{dy_2}{dx}=\frac{1}{EI}\left(-M_R(l-x)-\frac{P}{4}(l-x)^2\right)+C_3$$

さらに積分すると、

$$y_2=\frac{1}{EI}\left(\frac{M_R}{2}(l-x)^2+\frac{P}{12}(l-x)^3\right)-C_3(l-x)+C_4$$

このように荷重より右側の変位の式も得ることができました。

境界条件を用いて積分定数を求める

それでは境界条件を用いて、積分定数を求めましょう。

両端固定梁の場合の境界条件は、梁の両端が完全固定されている条件と荷重点の連続の条件から、下記の5つとなります。

$$y_1(0)=0$$

$$x=0で、\frac{dy_1}{dx}=0$$

$$y_2(l)=0$$

$$x=lで、\frac{dy_2}{dx}=0$$

$$x=\frac{l}{2}で\frac{dy_1}{dx}=\frac{dy_2}{dx}$$

これらを使って\(C_1~C_4\)を求め、未知数のまま残っていた\(M_{R1}\)も求めましょう。

\(y_1(0)=0\)

\(y_1\)はすでに導出していて、下記のように表されていましたね。

$$y_1=\frac{1}{EI}\left(\frac{Px^3}{12}+\frac{M_{R1}x^2}{2}\right)+C_1x+C_2$$

ここに\(x=0\)を代入すると、\(C_2=0\)となり、\(C_2\)が求まります。

\(x=0で、\frac{dy_1}{dx}=0\)

先ほどと同様に、たわみ角も求まっていて、

$$\frac{dy_1}{dx}=\frac{1}{EI}\left(\frac{Px^2}{4}+M_{R1}x\right)+C_1$$

この式に\(x=0\)を代入しますと、\(C_1=0\)となりますね。

\(y_2(l)=0\)

これも左側の条件と同様に解きます。

$$y_2=\frac{1}{EI}\left(\frac{M_R}{2}(l-x)^2+\frac{P}{12}(l-x)^3\right)-C_3(l-x)+C_4$$

と求まっていましたので、この式に\(x=l\)を代入すると、\(C_4=0\)を得ることができます。

\(x=lで、\frac{dy_2}{dx}=0\)

4つ目の境界条件です。これも簡単に求めることができます。

$$\frac{dy_2}{dx}=\frac{1}{EI}\left(-M_R(l-x)-\frac{P}{4}(l-x)^2\right)+C_3$$

この式に$x=l$を代入して、\(C_3=0\)となります。

以上より、積分定数はすべてゼロとなりました。

\(x=\frac{l}{2}で\frac{dy_1}{dx}=\frac{dy_2}{dx}\)

積分定数がゼロとなったので、\(\frac{dy_1}{dx},\frac{dy_2}{dx}\)は下記のようになります。

$$\frac{dy_1}{dx}=\frac{1}{EI}\left(\frac{Px^2}{4}+M_{R1}x\right)$$

$$\frac{dy_2}{dx}=\frac{1}{EI}\left(-M_R(l-x)-\frac{P}{4}(l-x)^2\right)$$

これらが\(x=\frac{l}{2}\)で一致するので、

$$\frac{1}{EI}\left(\frac{Pl^2}{16}+M_{R1}\frac{l}{2}\right)=\frac{1}{EI}\left(-M_{R1}\frac{l}{2}-\frac{Pl^2}{16}\right)$$

この式を整理すると、

$$M_{R1}=-\frac{Pl}{8}$$

となり、固定端のモーメントが求まります。

たわみの式は、

$$y_1=\frac{1}{EI}\left(\frac{Px^3}{12}-\frac{Plx^2}{16}\right)$$

$$y_2=\frac{1}{EI}\left(-\frac{Pl}{16}(l-x)^2+\frac{P}{12}(l-x)^3\right)$$

最大たわみ量は、これらの式のxに荷重点を\(\frac{l}{2}\)を代入することで求まって、代入すると、

$$y(\frac{l}{2})=-\frac{Pl^3}{192EI}$$

と計算することができます。

まとめ

以上、両端固定梁のたわみの式を導出しました。

少し長い記事となってしまいましたが、やっていることは、静定問題（片持ち梁や単純梁）の場合と同じで、

未知数が増えてしまっても、たわみの式を導出するときに積分する過程で求めることができます。

あとは頑張って計算するだけですので、しっかりと自分の手を動かしてみましょう。

初心者向けの教科書・参考書はこちら

材料力学の記事一覧はこちら