単純梁のBMDやSFDはわかったんだけど、たわみってどうやって求めるの?


片持ち梁のときと同じで、曲げモーメントの式を用いて計算すれば大丈夫だよ。
今回は単純梁に集中荷重をかけた場合のたわみの式を導出します。
求め方としては過去の記事で解説した片持ち梁のときと同じやり方ですので、そちらも是非参考にしていただければと思います。
また、動画でも解説しておりますのでそちらも是非ご覧になってください。単純梁のモデル
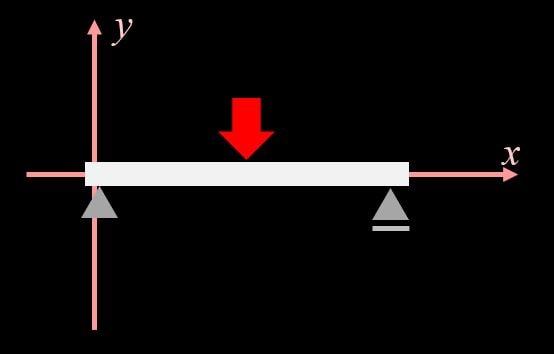
単純梁は上図のように片側がピン支点、もう片方がローラー支点となっているような梁です。
今回はこの単純梁の中央に荷重がかかったときを考えます。
曲げモーメントの式
曲げモーメントの式は下記のように表すことができます。
$$M(x)=\frac{EI}{ρ}$$
\(M\)が曲げモーメント、\(E\)がヤング率、\(I\)は断面2次モーメント、\(ρ\)は曲率半径です。
これらの解説については過去の記事で解説していますので参考にしていただければと思います。
単純梁-集中荷重の曲げモーメントの式は、前回の講義内容を引用すると、下記のように表すことができます。
荷重がかかっている点より左側の部分では、
$$M=Q×x=\frac{P}{2}x$$
緑のモーメントは梁内部に発生したせん断力によるモーメント、黄色の矢印は反力、赤丸は支点を指します。
次に荷重がかかっている点より右側の部分では、
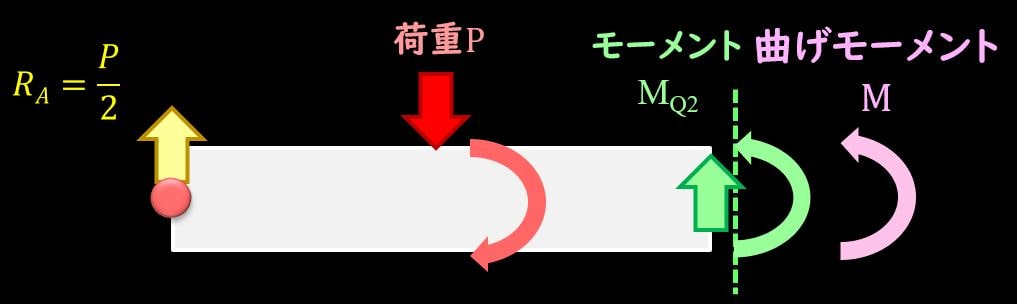
$$M=P×l-Q×x=P(l-\frac{x}{2})$$
赤の曲がっている矢印は荷重によるモーメントを指します。
このように、梁の左側と右側で場合わけをする必要があるわけです。
これらを使ってたわみの式を求めるのですが、曲げモーメントの式をもう少し変形します。
曲げモーメントの式は下記のようになっておりました。
$$M(x)=\frac{EI}{ρ}$$
この中の曲率半径\(ρ\)については、下記のように表すことができます。
$$\frac{1}{ρ}=\frac{d^2y}{dx^2}$$
この式を用いると、曲げモーメントの式は、下記のような線形微分方程式となります。
$$\frac{d^2y}{dx^2}=\frac{M}{EI}$$
この微分方程式を解けば、たわみ量がわかりますので、微分方程式を解いていきましょう。
たわみの式を導出する
それでは荷重のかかっている点の左側を考えてみましょう。
曲げモーメントの式は以下のようになります。
$$\frac{d^2y}{dx^2}=\frac{M(x)}{EI}$$
$$M(x)=\frac{P}{2}x$$
よって、
$$\frac{d^2y}{dx^2}=\frac{Px}{2EI}$$
と変形できます。
この微分方程式の解き方ですが、片持ち梁の時と同じで、直接積分形と呼ばれるものです。
解き方としては、両辺を積分して、積分定数を境界条件から求めていくことになります。
微分方程式の解き方
- 両辺を積分する
- 積分定数を境界条件(初期条件)によって求める
それでは両辺を積分してみましょう。
$$\frac{dy_1}{dx}=\int\frac{Px}{2EI}dx=\frac{Px^2}{4EI}+C_1$$
となります。もう一度積分すると、
$$y_1=\int(\frac{Px^2}{4EI}+C_1)dx=\frac{Px^3}{12EI}+C_1x+C_2$$
これで梁の左側の式について、積分できました。
次に、梁の右側の積分を行いましょう。
右側の曲げモーメントの式は、
$$M_2(x)=\frac{P}{2}(L-x)$$
となり、
$$\frac{d^2y}{dx^2}=\frac{P}{EI}(L-x)$$
となります。
この式についても積分を行うと、
$$\frac{dy}{dx}=\int\frac{P}{EI}(L-x)dx$$
ここで計算上のポイントですが、\((Lーx)\)は残した状態で積分します。
\(X=L-x\)とおくと、\(dX=-dx\)となりますので、右辺は、
$$\int\frac{P}{EI}(L-x)dx=\int\frac{PX}{EI}(-dX)=\frac{-PX^2}{2EI}+C_3$$
このようになります。\(x\)の式に戻すと、
$$\frac{dy_2}{dx}=-\frac{P(L-x)^2}{2EI}+C_3$$
このようになります。もう一度、両辺を積分すると、
$$y_2=\int(-\frac{P(L-x)^2}{2EI}+C_3)dx$$
再び、\(X\)を用いて右辺を表すと、
$$\int(-\frac{PX^2}{2EI}+C_3)(-dX)=\frac{PX^3}{6EI}-C_3X+C_4$$
この式を\(x\)の式に戻して、両辺を書くと、
$$y_2=\frac{P(L-x)^3}{6EI}-C_3(L-x)+C_4$$
このようになります。
以上より、積分定数である\(C_1~C_4\)を求める必要があることがわかりますね。
ここからは積分定数を求めるために、境界条件を使っていきましょう。
境界条件により積分定数を求める
さて、境界条件ですが、単純梁の場合は下記のようになります。
$$y_1(0)=0$$
$$y_2(L)=0$$
$$y_1(\frac{L}{2})=y_2(\frac{L}{2})$$
$$\frac{dy_1}{dx}=\frac{dy_2}{dx}$$
これらを文章で書くと下記のようになります。
- 梁の端(支点の部分)ではy方向の変位量がゼロになる
- 荷重がかかっている点では\(y_1\)と\(y_2\)が等しくなる
- 荷重がかかっている点ではたわみ角も等しくなる
これらを使って、積分定数を求めていきましょう。
\(y_1(0)=0, y_2(L)=0\)
これらの境界条件から、\(C_2=0,C_4=0\)となります。
\(LーX\)を残して積分したことで、この部分の計算が楽になりましたね。
荷重がかかっている点での条件
$$y_1(\frac{L}{2})=y_2(\frac{L}{2})$$
$$\frac{dy_1}{dx}=\frac{dy_2}{dx}$$
上記2つを用いて、残りの積分定数を求めます。
まず一つ目の式の左辺、右辺を見ていきましょう。
$$y_1(\frac{L}{2})=\frac{P}{12EI}\left(\frac{L}{2}\right)^3+\frac{C_1L}{2}$$
$$y_2(\frac{L}{2})=\frac{P}{12EI}\left(\frac{L}{2}\right)^3-\frac{C_3L}{2}$$
これらがイコールとなるので、
$$\frac{P}{12EI}\left(\frac{L}{2}\right)^3+\frac{C_1L}{2}=\frac{P}{12EI}\left(\frac{L}{2}\right)^3-\frac{C_3L}{2}$$
式を整理すると、
$$C_1+C_3=0$$
となります。
次に、たわみ角が等しい条件を考えましょう。
$$\frac{dy_1}{dx}=\frac{P}{4EI}\left(\frac{L}{2}\right)^2+C_1$$
$$\frac{dy_2}{dx}=\frac{-P}{4EI}\left(\frac{L}{2}\right)^2+C_3$$
これらがイコールとなるので、
$$\frac{P}{4EI}\left(\frac{L}{2}\right)^2+C_1=\frac{-P}{4EI}\left(\frac{L}{2}\right)^2+C_3$$
これも式を整理すると
$$C_1-C_3=\frac{-P}{2EI}\left(\frac{L}{2}\right)^2$$
このようになります。
それでは\(C_1\)と\(C_3\)を連立方程式を解くことで求めていきましょう。
$$C_1+C_3=0$$
$$C_1-C_3=\frac{-P}{2EI}\left(\frac{L}{2}\right)^2$$
2つの式を足してあげると、
$$2C_1=\frac{-P}{2EI}\left(\frac{L}{2}\right)^2$$
両辺を2で割って、\(C_1\)を求めると、
$$C_1=\frac{-P}{4EI}\left(\frac{L}{2}\right)^2$$
また、\(C_1+C_3=0\)なので、
$$C_3=\frac{P}{4EI}\left(\frac{L}{2}\right)^2$$
と積分定数を求めることができます。
以上より、
$$y_1=\frac{Px^3}{12EI}-\frac{P}{4EI}\left(\frac{L}{2}\right)^2x$$
$$y_2=\frac{P(L-x)^3}{6EI}-\frac{P}{4EI}\left(\frac{L}{2}\right)^2$$$$\frac{dy_1}{dx}=\frac{Px^2}{4EI}-\frac{P}{4EI}\left(\frac{L}{2}\right)^2$$
$$\frac{dy_2}{dx}=-\frac{P(L-x)^2}{2EI}+\frac{P}{4EI}\left(\frac{L}{2}\right)^2$$最大たわみを求める
ここまでで、任意の位置でのたわみ量\(y_1,y_2\)が求まったわけなのですが、最大たわみ量を計算しておきます。最大たわみが発生する場所はどの部分になるでしょうか?
それは、梁の傾き(たわみ角)がゼロになる点となります。
つまり、微分した式がゼロとなればよいので、 $$\frac{dy_1}{dx}=\frac{Px^2}{4EI}-\frac{P}{4EI}\left(\frac{L}{2}\right)^2=0$$
となるような\(x\)を求めればよいことになります。式を整理すると
$$\frac{P}{4EI}x^2=\frac{P}{4EI}\left(\frac{L}{2}\right)^2$$この式を解くと、
$$x=\frac{L}{2}$$つまり、荷重がかかっている点で、最大たわみが発生する、ということになります。
ちなみに、梁中央以外に荷重がかかっている場合は、最大たわみが発生する点は荷重がかかっている点と異なってきますので、しっかりと微分した式=0を計算するようにしましょう。
さて、最大たわみ量を計算するために、\(y_1\)の式に\(x=\frac{L}{2}\)を計算すると、
$$y_1\left(\frac{L}{2}\right)=\frac{P}{12EI}\left(\frac{L}{2}\right)^3-\frac{P}{4EI}\left(\frac{L}{2}\right)^2\left(\frac{L}{2}\right)$$この式を整理すると、
$$y_1\left(\frac{L}{2}\right)=\frac{-PL^3}{48EI}$$となります。
以上で単純梁の最大たわみ量を計算することができました。まとめ
本日は単純梁のたわみの式を解説しました。単純梁の等分布荷重のたわみの式
$$y_1=\frac{Px^3}{12EI}-\frac{P}{4EI}\left(\frac{L}{2}\right)^2x$$
$$y_2=\frac{P(L-x)^3}{6EI}-\frac{P}{4EI}\left(\frac{L}{2}\right)^2$$
たわみの式の導出の仕方
- 曲げモーメント図(BMD)を求める
- 曲げモーメントの式を積分し、境界条件から積分定数を求める
曲げモーメントの式
$$M=\frac{EI}{ρ}$$
計算自体は片持ち梁と大きく変わりませんので、流れをしっかりと理解しておきましょう。
初心者向けの教科書・参考書はこちら
材料力学の記事一覧はこちら
