梁のたわみの式ってなんかいろいろ種類あるみたいなんだけど、覚えないといけないの?


BMDと曲げモーメントの式から導出できるし、ググったら公式は出てくるから、丸暗記はあまりオススメできないね。
ということで、今日は、梁のたわみの式を曲げモーメントの式から導出します。
曲げモーメントの式から導出するやり方を理解することで、色んな梁のたわみの計算に対応できるようになりますので、しっかり理解しておきましょう。
今回は片持ちはりを例にとって解説して行きます。
途中、微分方程式を解く部分がありますが、初心者でもわかるように解説しますので、ご安心ください。
微分方程式については過去に解説していますので、そちらも是非参考にしていただければと思います。
動画でも解説していますので、下記を是非ご覧ください。
モデルとBMD、曲げモーメントの式
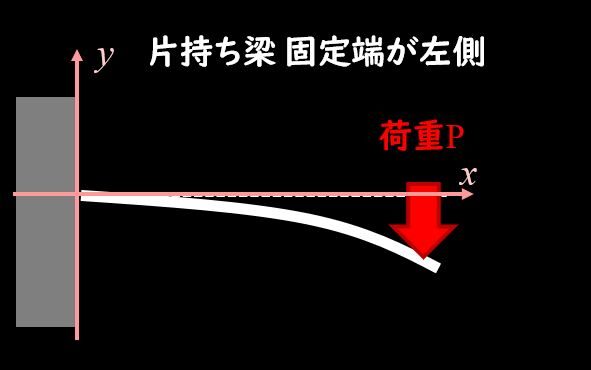
まず復習としてBMD、曲げモーメントの式についておさらいしましょう。
BMD(曲げモーメント図)
梁の曲げについて解説して行きますので、基本的な内容として、BMDを理解しておく必要があります。
過去の記事で解説していますので、詳細はそちらを参考にしてもらうとして、
BMDは梁にかかっている曲げモーメントの分布を示しているものでした。
片持ち梁の場合は、下記のように直線的に変化しますね。
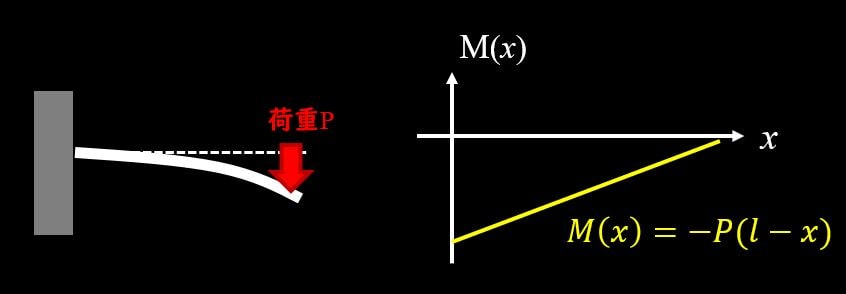
この曲げモーメントが大きな点で大きな曲げ応力が発生するので、曲げ変形が起こった時に、どこから壊れるかが分かるわけです。
曲げモーメントの式
曲げモーメントの式は曲率半径を用いると下記のように表されます。
$$M(x)=\frac{EI}{ρ}$$
\(E\)はヤング率、\(I\)は断面二次モーメント、\(ρ\)は曲率半径を示します。
ここで曲率半径\(ρ\)が下記のような関係にあることを使います。
$$\frac{1}{ρ}=\frac{d^2y}{dx^2}$$
これを使うと、曲げモーメントの式は、下記のような微分方程式となります。
$$\frac{d^2y}{dx^2}=\frac{M(x)}{EI}$$
こちらも過去の記事で解説していますので、そちらを参考にしていただければと思います。
曲げモーメントの式を解く
さて、片持ち梁のBMDから、曲げモーメントはxの関数として下記のように表されます。
$$M(x)=-P(l-x)$$
この式を曲げモーメントの式へ代入してみましょう。
$$\frac{d^2y}{dx^2}=\frac{-P(l-x)}{EI}$$
これは2階非同次線形微分方程式と呼ばれるものですが、解き方は非常にシンプルです。
積分型と呼ばれる解き方となり、解き方は
微分方程式の解き方
- 両辺を積分する
- 積分定数を境界条件(初期条件)によって求める
となります。
それでは両辺を積分するところからやっていきましょう。
両辺を積分する
まず1回目の積分をしてみましょう。
$$\int\frac{d^2y}{dx^2}dx=\int\frac{-P(l-x)}{EI}dx$$
この積分を計算するわけですが、左辺は、
$$\int\frac{d^2y}{dx^2}dx=\frac{dy}{dx}+A_1$$
\(A_1\)は積分定数です。
次に右辺を計算すると、
$$\int\frac{-P(l-x)}{EI}dx=\frac{-Pl}{EI}x+\frac{P}{2EI}x^2+A_2$$
\(A_2\)も積分定数です。
積分定数を\(A\)としてまとめると、曲げモーメントの式を1回積分した式は、
$$\frac{dy}{dx}=\frac{-Pl}{EI}x+\frac{P}{2EI}x^2+A$$
このようになります。
何とも複雑と感じたかもしれませんが、このまま行きます。
次に2回目の積分を実施してみましょう。
$$\int\frac{dy}{dx}dx=\int\left(\frac{-Pl}{EI}x+\frac{P}{2EI}x^2+A\right)dx$$
同様に左辺の積分を実行してみると
$$\int\frac{dy}{dx}dx=y+B_1$$
\(B_1\)は積分定数です。
右辺の計算については、
$$\int\left(\frac{-Pl}{EI}x+\frac{P}{2EI}x^2+A\right)dx=\frac{-Pl}{2EI}x^2+\frac{P}{6EI}x^3+Ax+B_2$$
\(B_2\)も積分定数です。これらをまとめると、
$$y=\frac{-Pl}{2EI}x^2+\frac{P}{6EI}x^3+Ax+B$$
このように\(y\)の式がもとまりましたので、未知の定数である\(A\)と\(B\)について求めに行きましょう。
境界条件

片持ち梁の境界条件ですが、上記のように座標軸をとると、下記のようになります。
$$θ(0)=0, y(0)=0$$
\(θ\)はたわみ角で、梁の曲がり具合を示します。
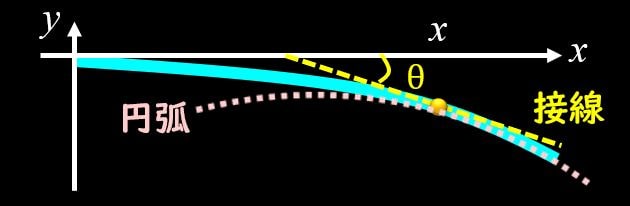
梁の一部を円弧で近似し、円に接線を引いた時、その接線と\(x\)軸がなす角をたわみ角と呼びます。
この辺りは過去の記事でも解説していますので、参考にしていただければと思います。
さて、ふたつの境界条件が何を意味しているかというと、片持ち梁の固定端では曲がりもしないし、動きもしない、ということを示しています。
片持ち梁の固定端が完全固定になっているので、このような境界条件になるわけです。
これらの条件を使って、たわみの式に出てきた積分定数を計算してみましょう。
積分定数を求める(たわみ角について)
境界条件の一つ目、\(θ\)ですが、これはとある近似を用いることで、先ほどのたわみの式へ適応させることができます。
結論的には下記のような関係式を使います。
$$\frac{dy}{dx}=tanθ≒θ$$
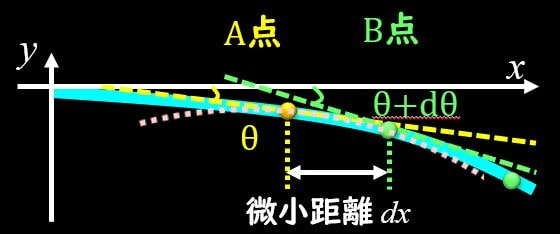
たわみ角は上図のように、接線と\(x\)軸のなす角なので、接線の傾きは\(tanθ\)となります。
一方、この傾きは\(\frac{dy}{dx}\)と表すこともできるので、
$$\frac{dy}{dx}=tanθ$$
と表すことができます。
ここまできて、ある近似を用いるのですが、
それは材料力学であったり、構造力学の前提ともなっているθ<<1という条件を用います。
たわみ角θが非常に小さい、すなわち微小なたわみ量を考えた時、\(tanθ≒θ\)となります。
よって、先ほど述べた式が成り立つわけですね。
$$\frac{dy}{dx}=tanθ≒θ$$
積分定数を求める
それでは、\(y\)を\(x\)で1回微分したものがθである、という関係式と境界条件を用いて積分定数を求めて行きましょう。
$$\frac{dy}{dx}=\frac{-Pl}{EI}x+\frac{P}{2EI}x^2+A$$
この式が境界条件によりゼロとならなければいけませんので、
$$θ(0)=A=0$$
となります。
同様にもう一つの境界条件を用いてBを求めます。
\(y\)の式は下記のようになっておりました。
$$y=\frac{-Pl}{2EI}x^2+\frac{P}{6EI}x^3+Ax+B$$
ここに境界条件である\(y(0)=0\)と先ほど求めた\(A=0\)を入れると、
$$y(0)=B=0$$
となります。
よって、\(y\)の式は下記のようになります。
$$y(x)=\frac{-Pl}{2EI}x^2+\frac{P}{6EI}x^3$$
ここで、最大たわみ量δは\(x=l\)の時ですので、
$$δ=\frac{-Pl^3}{3EI}$$
となります。
このように微分方程式を解くことで、たわみの式を導出することができます。
まとめ
曲げモーメントの式からたわみの式を導出しました。
片持ち梁の集中荷重のたわみの式
$$y(x)=\frac{-Pl}{2EI}x^2+\frac{P}{6EI}x^3$$
最大たわみ量δ
$$δ=\frac{-Pl^3}{3EI}$$
たわみの式の導出の仕方
- 曲げモーメント図(BMD)を求める
- 曲げモーメントの式を積分し、境界条件から積分定数を求める
曲げモーメントの式
$$M=\frac{EI}{ρ}$$
今回は片持ち梁を用いて説明しましたが、他の梁でも基本的には同様ですので、まずはこの流れをしっかりと理解しておきましょう。
初心者向けの教科書・参考書はこちら
材料力学の記事一覧はこちら
