曲がり具合を曲率半径で表すって言っても全然イメージわかないんだけど…


それじゃあ今日は曲率半径について解説するね。
本日は曲率半径について解説します。
曲げモーメントの式で曲率半径が含まれた状態で出てくるのですが、このイメージが湧かない人が多いと思いますので、しっかりと解説しますね。
曲げについては過去の記事で解説していますので、下記を参考にしていただければと思います。
動画でも解説していますので、是非参考にしていただければと思います。
曲げモーメントの式
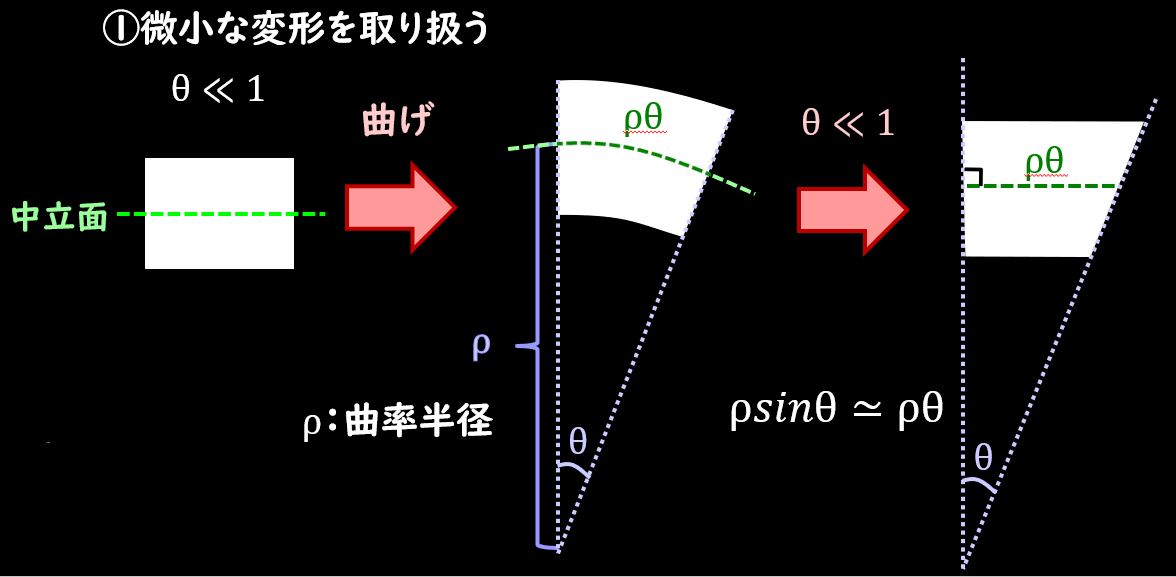
まず、材料力学の前提として、『微小な変形を取り扱う』、という点と、梁を曲げた際に『断面の形状が維持される』という仮定があることに注意してください。
これは過去の記事でも解説していますので、気になる方はそちらを見ていただければと思います。これらの仮定を用いて、微小な変形による近似\(sinθ≃θ\)などを用いて計算していくと、曲げモーメント\(M\)と曲率半径\(ρ\)の関係性は下記のようになります。
$$M=\frac{EI}{ρ}$$
\(E\)は縦弾性係数(ヤング率)、\(I\)は断面2次モーメントです。
\(EI\)は曲げ剛性とも呼び、部材全体の曲がりにくさを示しています。
分母の\(ρ\)が曲率半径で、部材の曲がり具合を示しており、
\(ρ\)が小さい(曲がり具合が大きい)と曲げモーメントが大きくなることが、式からはわかりますね。
曲率半径と曲がり具合のイメージ
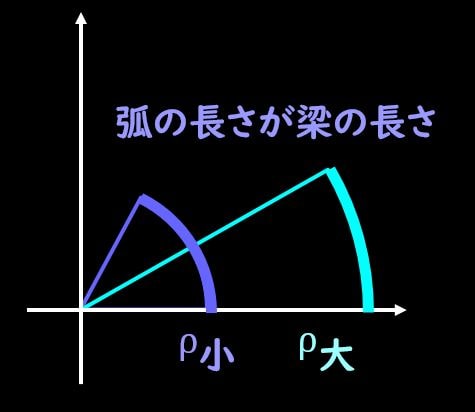
それでは曲率半径が小さいときと大きいときで比較してみましょう。
曲率半径が小さいと、図の濃い青線のような円弧の弧の部分が梁となります。
一方で曲率半径が大きい場合、図の水色の円弧の弧の部分が梁となります。
さて、濃い青と水色の梁、どちらが大きく曲がっているでしょうか?
これは濃い青の方、すなわち曲率半径が小さい方が曲がっていますね。

身近な例だと、道路のカーブの急さを示すのにR400とかR○○という表記を使いますね。
これは半径\(R\)が小さいほうが急なカーブになっていることを示していて、曲率半径と全く同じ意味です。
曲率半径の数学的な意味
曲率半径をもう少し深掘りして、数学的にどう扱うかについて解説しておきます。
材料力学でよく使う式は下記です。
$$\frac{1}{ρ}=κ=\frac{d^2x}{dy^2}$$
\(κ\)は曲率を示します。
曲率と曲率半径の関係については、証明もできますが少し煩雑な過程になりますので、定義として覚えた方がよいです。
曲率や曲率半径の逆数が、2回微分の形になっていることが重要で、これは微小角度の変形であることの近似を使うことで、上式のような関係になっています。
それでは、なぜこうなるかを見ていきましょう。
θとdθが示す部分

上図のように、水色の梁を円弧で近似することを考えます。円弧で近似しているのはA点とB点の間で、微小な距離となっています。ここで、\(θ\)や\(dθ\)というパラメータが出てくるのですが、これらがどこを示しているかが非常に重要ですので、確認しておきましょう。
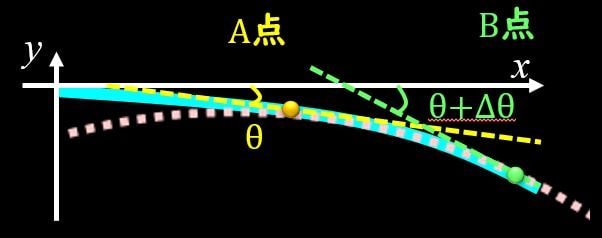
上図のように、A点での円の接線と\(x\)軸がなす角を\(θ\)、B点での円の接線と\(x\)軸がなす角を\(θ+⊿θ\)となります。
次にA点とB点の距離を近くして微小距離としたとき、どのようになるかを考えます。
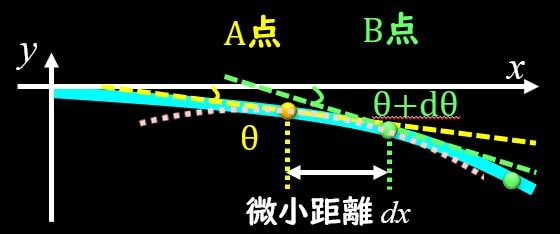
\(dθ\)は微小距離だけ離れた点の角度の変化となりますので、微小な角度\((dθ<<1)\)となります。また、材料力学の前提として、変形は微小である、という前提で取り扱うので、\(θ\)も微小な角度になります\((θ<<1)\)。
円弧の近似
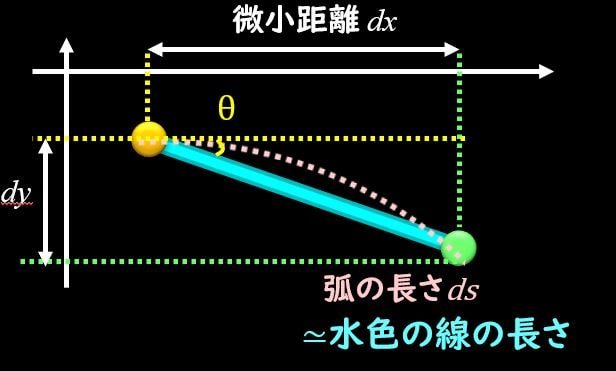
A点とB点を拡大した図を上図で示しています。
弧の長さを\(ds\)とすると、\(dθ\)が微小な角度なので、水色の直線と同じ長さと近似することができます。 曲率半径を\(ρ\)とすると、AB間の円弧の長さは、
$$ds=ρdθ$$
直線近似すると、
$$ρsindθ≃ρdθ$$となって水色の直線の長さと円弧の長さは一致します。
さて、水色の直線の長さは、微小距離の\(dx\)と\(dy\)を使って下記のようにも表すことができます。
$$ds=\sqrt{dx^2+dy^2}$$
これを少し変形すると、
$$\sqrt{dx^2+dy^2}=\sqrt{1+\left(\frac{dy}{dx}\right)^2}dx$$
ここで、\(\frac{dy}{dx}\)は\(θ\)となります。
これは\(θ\)が微小角であり、\(\frac{dy}{dx}=tanθ\)、\(tanθ≃θ\)となるためです。
また、\(θ\)は微小角で、2乗するとゼロとして近似することができます。
よって、ルートの中が1となって
$$ds≃dx$$と近似することができ、\(ds=ρdθ\)であったので、
$$dx=ρdθ$$となります。この式を変形すると、
$$\frac{1}{ρ}=\frac{dθ}{dx}=\frac{d^2y}{dx^2}$$
となります。
これで\(ρ\)や\(θ\)の式が\(x\)や\(y\)を使って表すことができましたね。
曲げの式へ代入してみる
曲げの式がどのような形だったかというと、下記のような形でしたね。
$$M=\frac{EI}{ρ}$$ ここに先ほどの\(\frac{1}{ρ}=\frac{d^2y}{dx^2}\)を代入してみましょう。
$$\frac{d^2y}{dx^2}=\frac{M}{EI}$$
このようになります。
\(E\)も\(I\)も\(y\)や\(x\)に依存しないパラメータですので(材料力学の基礎的な分野では一定とみなして計算することがほとんど)、
\(M\)について考えてみましょう。
\(M\)は曲げモーメントで、\(x\)方向で変化するため、\(x\)の関数となります。
つまり、\(M(x)\)という形で書くことができて、この\(M(x)\)さえわかれば、代入して、2階の線形微分方程式を解くことで、たわみの式が求まるわけですね。

例えば上図のような片持ち梁だと、曲げモーメント\(M(x)\)は
$$M(x)=-P(l-x)$$
となるので、これを先ほどの曲げの式に代入すると、$$\frac{d^2y}{dx^2}=\frac{P}{EI}(x-l)$$
このように表すことができ、この微分方程式を解くことで、片持ち梁のたわみの式を導出することができます。この導出については別記事で解説しますので、そちらを参考にしていただければと思います。
まとめ
曲率半径から曲げの式への導出までを行いました。ポイント
曲率半径の近似式
$$\frac{1}{ρ}=κ=\frac{d^2x}{dy^2}$$
曲げモーメントの式
$$M=\frac{EI}{ρ}$$
片持ち梁の場合
$$\frac{d^2y}{dx^2}=\frac{P}{EI}(x-l)$$
\(θ\)が微小角であることと、\(θ\)がどこの部分を表しているかをしっかりと理解しておけば、導出までそれほど難しい話ではないので、流れをしっかりとつかんでおきましょう。
初心者向けの教科書・参考書はこちら
材料力学の記事一覧はこちら
次の記事 → 材料力学 初心者向け 曲げモーメント図とせん断力図を描く BMDとSFDの書き方
