なんか荷重が梁全体にかかっているんだけど、これってどうやって解くの?


いわゆる分布荷重の問題だね。今日は片持ち梁の等分布荷重のBMDについて解説するね。
今回は片持ち梁に等分布荷重をかけた場合の曲げモーメント図(BMD)についてです。
これまでは集中荷重の場合を解説してきましたが、分布荷重もよく見る例となりますので、しっかりと理解しておきましょう。
まずは曲げを語る上で欠かせない、曲げモーメント図(BMD)の書き方をやっていきましょう。
集中荷重の場合は下記の過去記事を参考にしていただければと思います。
また、下記の動画でも解説していますので是非参考にしていただければと思います。
モデル
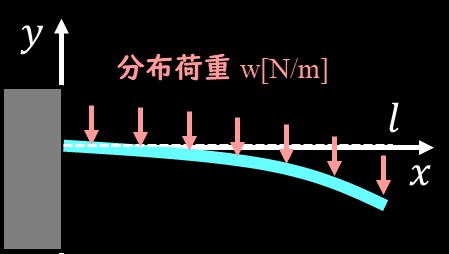
上図のように片持ち梁全体に分布荷重が発生している場合を考えてみましょう。
梁の長さは\(l\)、荷重は\(w[N/mm]\)と単位長さあたりに発生している荷重を考えます。
BMDの書き方のおさらい
BMDの書き方は過去の記事でも詳細を解説していますので、そちらを参考にしていただければと思います。
BMDの書き方は下記の5ステップで描くことができるのでした。
BMDの描き方
- 座標軸をとる
- 外力のつり合いの式を立てる
- 切り出して切り出した部分のせん断力を書く
- せん断力によるモーメントを書く
- 切り出して面に注目して、せん断力によるモーメントにつり合うように、曲げモーメントを書く
座標軸の取り方については、今回は下図のようにとって考えますので、2つ目のつり合いの式を考えるところからスタートしましょう。

つりあいの条件を考える
片持ち梁において、考えなければいけないつり合いの条件は、\(y\)方向の力のつり合いとモーメントのつり合いです。
\(x\)方向には力がかかっていないので、今回は無視します。
\(y\)方向のつり合い
\(y\)方向のつり合いですが、単位長さあたりに\(w\)の荷重がかかっているので、長さ\(l\)の梁には\(w\)lの力がかかっていることになります。
外力はこの分布荷重のみで、この外力だけだと梁は力のつり合いが保たれておらず、静止できていないことになります。
そこで、片持ち梁の場合、固定端からの反力を考えることで、力のつり合いを保つことができるのでした。
梁の支持の仕方によって、反力やモーメントを発生させることができるかどうかは決まっておりますので、下表をしっかりと頭に入れておきましょう。

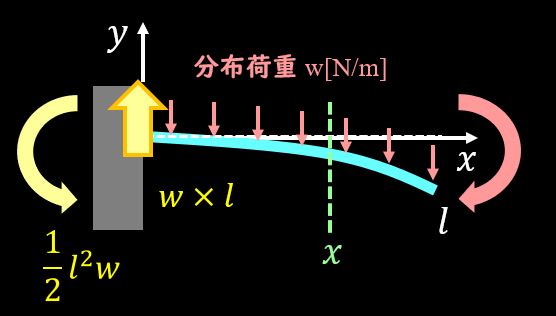
今回は固定端の部分に\(wl\)の反力が発生して、力のつり合いを保っていることになりますね。
モーメントのつりあい
さて、分布荷重がかかっている時のモーメントはどのように表記されるでしょうか?
ここが1番のポイントです。
支点を固定端において、支点から見た時のモーメントを考えてみましょう。
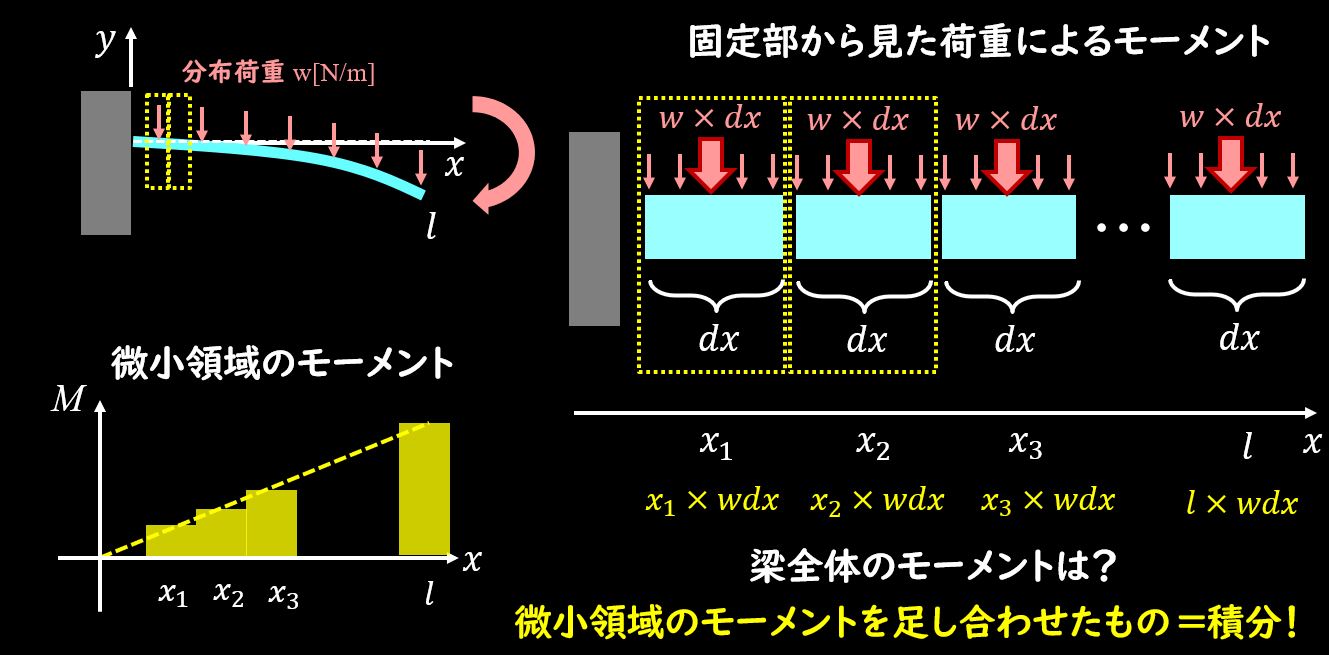
モーメントは力×距離で表されますが、力の部分が梁全体にかかっている状態なわけです。
こういう場合は、とある\(x\)座標の微小領域を見て、積分して全体を表す、ということを行います。
梁の幅は微小距離\(dx\)です。
この微小領域にかかっている力は\(w×dx\)となりますね。
つまり、このとある\(x\)座標での微小領域に発生しているモーメントは\(x×w×dx\)となります。
あとはこの微小領域のモーメントを\(0〜l\)まで積分してあげると、等分布荷重によるモーメントがもとまりますね。
$$\int^l_0x×w×dx=\frac{1}{2}l^2w$$
このようになります。
さて、このモーメントだけであれば、梁は回転してしまうので、固定端につりあうようなモーメントを発生させなければいけません。
つまり、固定端には下図の黄色の矢印のようなモーメントが発生することになります。

切断してせん断応力を書く
次のステップとして、梁の途中を切り出し、せん断応力を考えてみましょう。
上図の緑の点線のように、とある\(x\)座標で梁を切り出します。
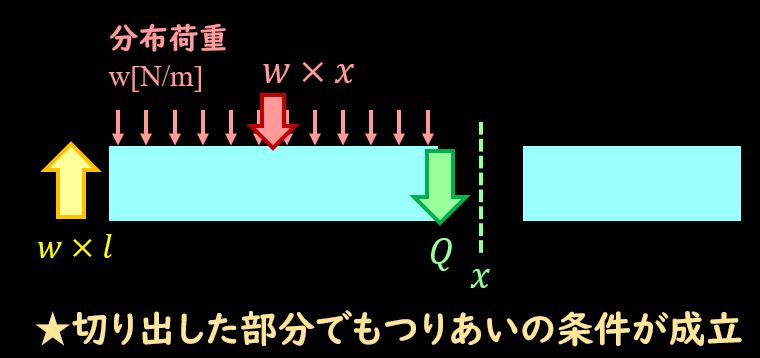
この切り出した状態でも、力のつり合いやモーメントのつり合いが成立しなければいけませんので、
まずは力のつりあいについて考えてみましょう。
切り出した座標位置は\(x\)なので、分布荷重から受ける力は\(w×x\)となりますね。
また、固定端には上向きに\(w×l\)の力が反力として発生していますので、分布荷重と比較すると、反力の方が大きくなっていることがわかります。
このままだと、力のつり合いが保たれない、ということで、切断面に下向きの力をかけて、つり合いを保つようにします。
下向きのせん断力が正であるとすると、せん断力\(Q\)は、
$$Q=wl-wx=w(l-x)$$
となります。
この式を使ってSFD(せん断力図)を書くと、下記のようになりますね。

せん断力によるモーメントを書く
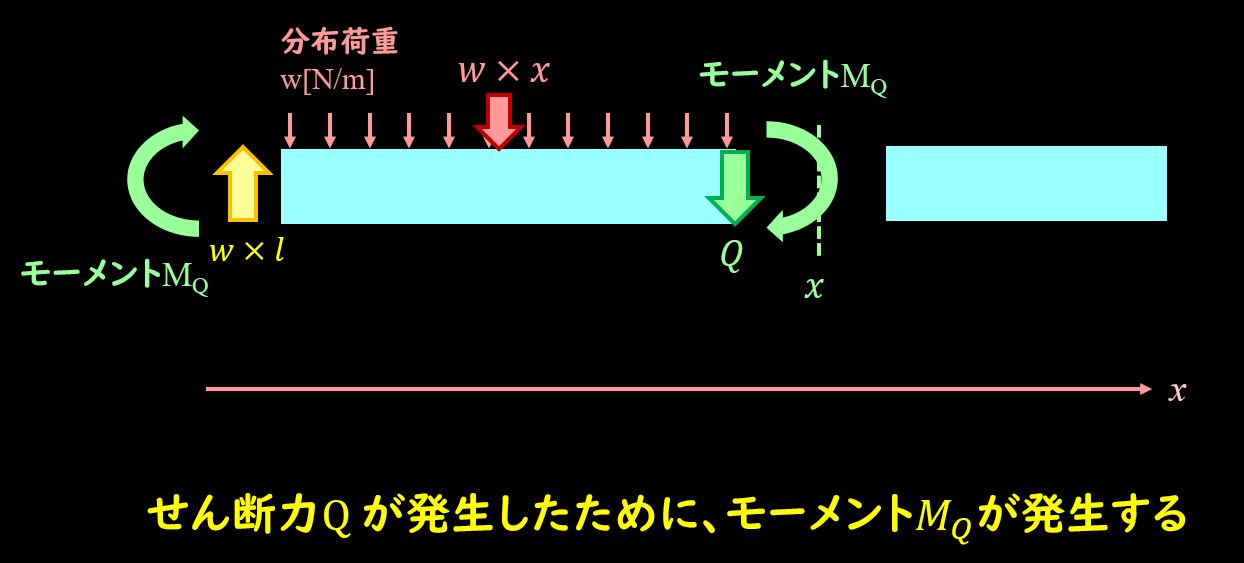
せん断力が切断面に発生していますので、せん断力によるモーメントを書きましょう。
固定端の位置を支点で考えます。
切断面の座標が\(x\)でせん断力が\(Q\)なので、せん断力によるモーメントを\(M_Q\)とすると、
$$M_Q=Q×x=w(l-x)x$$
となります。
切断した部分のモーメントのつり合い
最後のステップです。
切り出した部分のモーメントのつり合いを考え、BMDを描きましょう。
切り出した部分の中のとある座標\(X\)を使って、分布荷重によるモーメントを考えます。
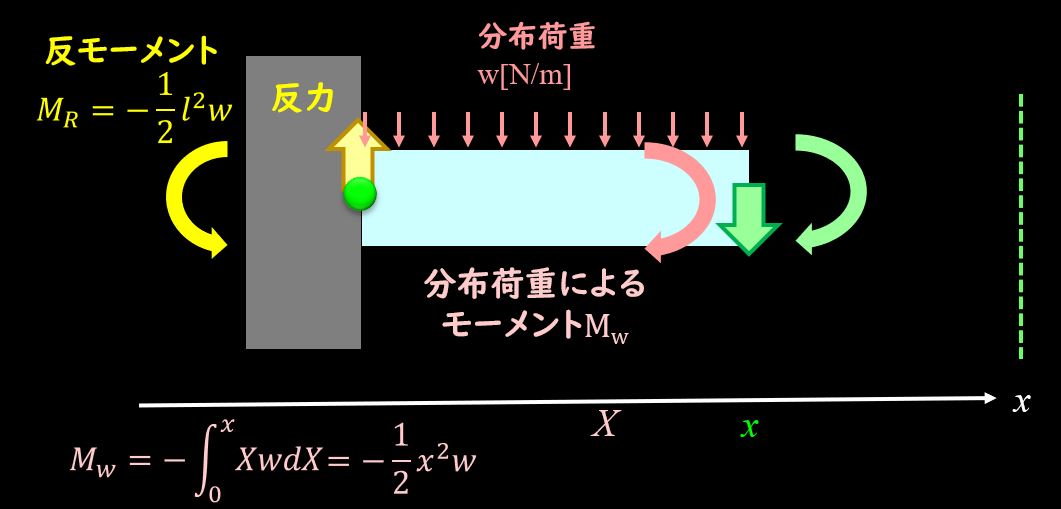
これは梁全体のモーメントを考えたときと同じやり方で、積分して求めることになります。
とある\(X\)座標での微小領域\(dX\)を考えると、この微小領域での力は
$$w×dX$$
と表すことができますので、微小領域に発生するモーメントは距離\(X\)をかけて、
$$X×w×dX$$
あとはこれを\(0〜x\)まで積分すれば分布荷重によるモーメントはもとまって、
$$\int^x_0XwdX=\frac{1}{2}x^2w$$
となります。
梁に発生しているモーメントは、分布荷重によるモーメント、固定端に発生しているモーメント、切断面に発生しているせん断力によるモーメントとなります。
これらが吊り合うように切断面に発生している曲げモーメントをMとすると、モーメントのつり合いから、
$$M=\frac{1}{2}x^2w-\frac{1}{2}l^2w+w(l-x)x$$
この式から曲げモーメントを求めましょう。
$$M=-\frac{w}{2}(l-x)^2$$
曲げモーメント図を書くと、下図のようになります。
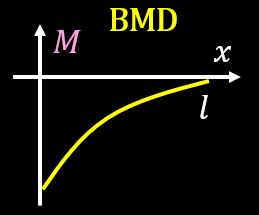
以上から等分布荷重の場合、BMDは2次関数となります。
まとめ
本日は片持ち梁に等分布荷重が発生している場合を解説しました。
片持ち梁 等分布荷重のBMD


片持ち梁の曲げモーメントの式
$$M=-\frac{w}{2}(l-x)^2$$
BMDの描き方
- 座標軸をとる
- 外力のつり合いの式を立てる (積分して、梁全体に発生するモーメントを考える)
- 切り出して切り出した部分のせん断力を書く
- せん断力によるモーメントを書く
- 切り出して面に注目して、せん断力によるモーメントにつり合うように、曲げモーメントを書く
分布荷重を考える場合は、積分をする必要がありますが、とある微小領域を考えて、積分するイメージをしっかりと理解しておきましょう。
初心者向けの教科書・参考書はこちら
材料力学の記事一覧はこちら
