曲げ応力ってそもそもなんで三角形の形になっているの


これは材料力学の問題の前提条件が知識として必要なので、今日は曲げ応力の詳細を説明するね。
本日は曲げ応力について解説します。
過去の記事で初心者向けに曲げ応力・曲げ応力度についての解説をしています。材料力学 初心者向け-曲げ応力・応力度についてわかりやすく解説
曲げ応力については下記の動画でも解説していますので、参考にしていただければと思います。梁を曲げた時の応力分布
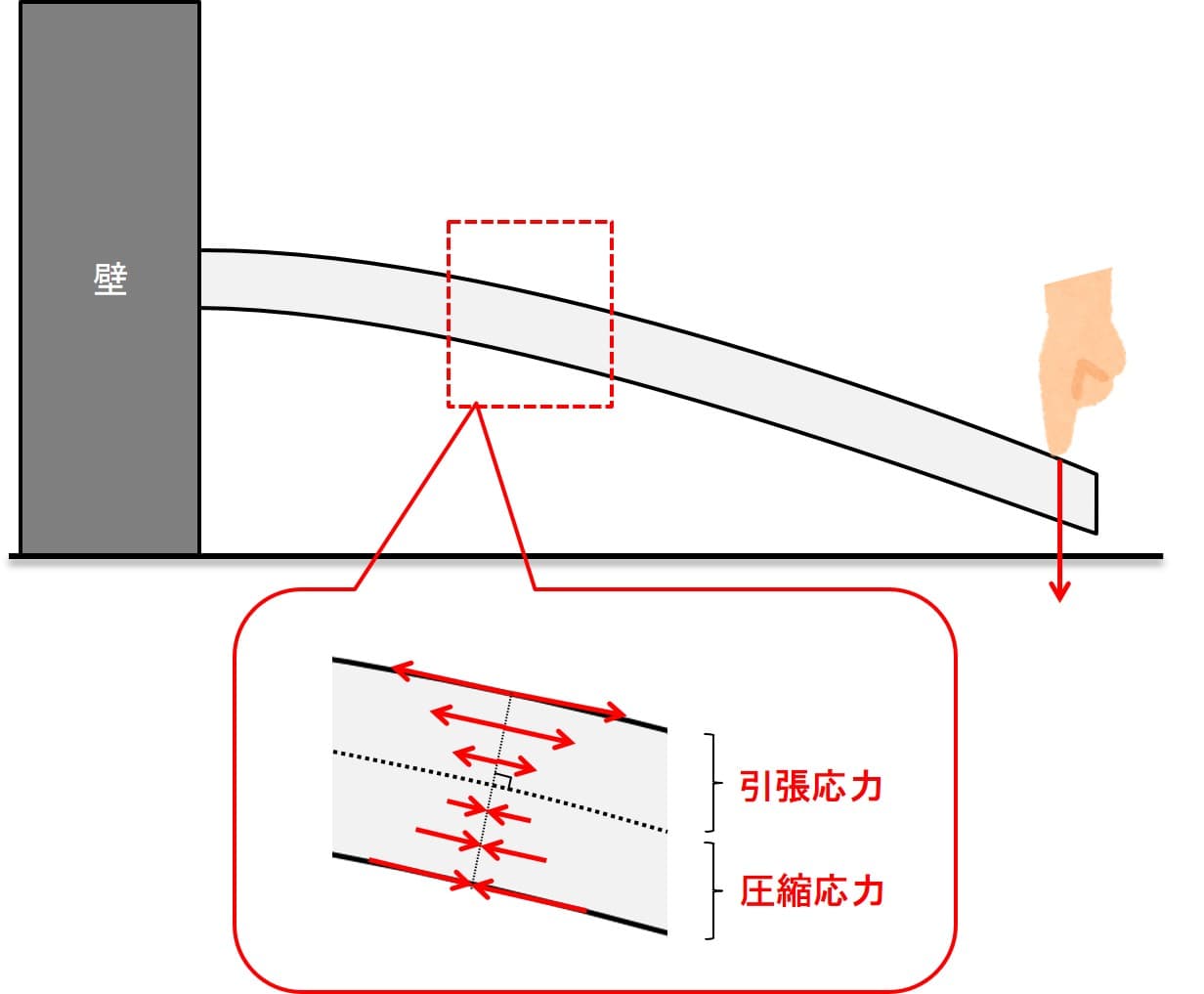
上図のように梁を曲げると、部材には曲げ応力が発生します。
それではなぜこのような応力分布になるかについて理解していきましょう。
材料力学の問題の前提条件
ポイント
- 微小な変形を取り扱っている
- オイラーベルヌーイの梁を家仮定
上記二つの仮定を用いているために、応力分布は直角三角形が2つ繋がったような形に分布します。
微小な変形とは
これは近似計算を用いるための条件です。
微小な変形量の中でも曲げ応力を理解する上では、『微小な角度』が重要です。
三角関数の微小角度の場合の近似式を下記に示しておきますね。
\(θ<<1\)のとき
$$sinθ=θ$$
$$cosθ=1$$
$$tanθ=θ=\frac{dx}{dy}$$
これらはしっかりと覚えておきましょう。
オイラーベルヌーイの梁
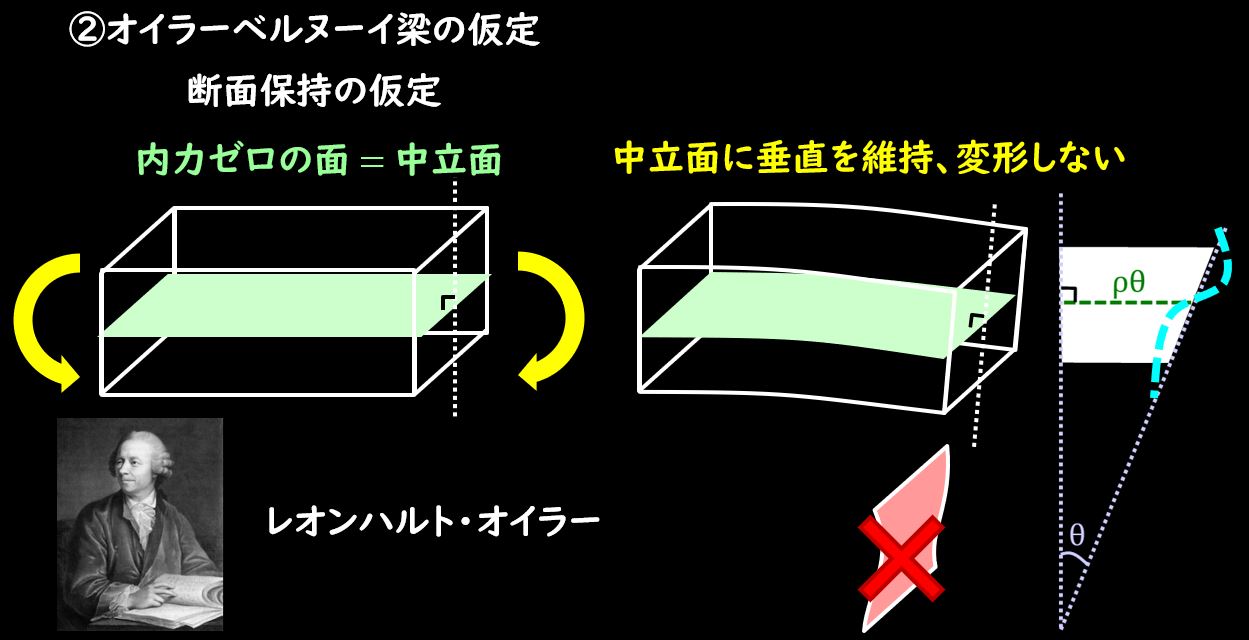
これは、『中立軸に垂直な面は、曲げ変形しても平面を保っている』ような梁のことを言います。
上図のように、曲げた時に平面を保てていないと、計算が複雑になりそうな予感がしませんか?
これも計算しやすくするための仮定となります。
曲げ応力の分布
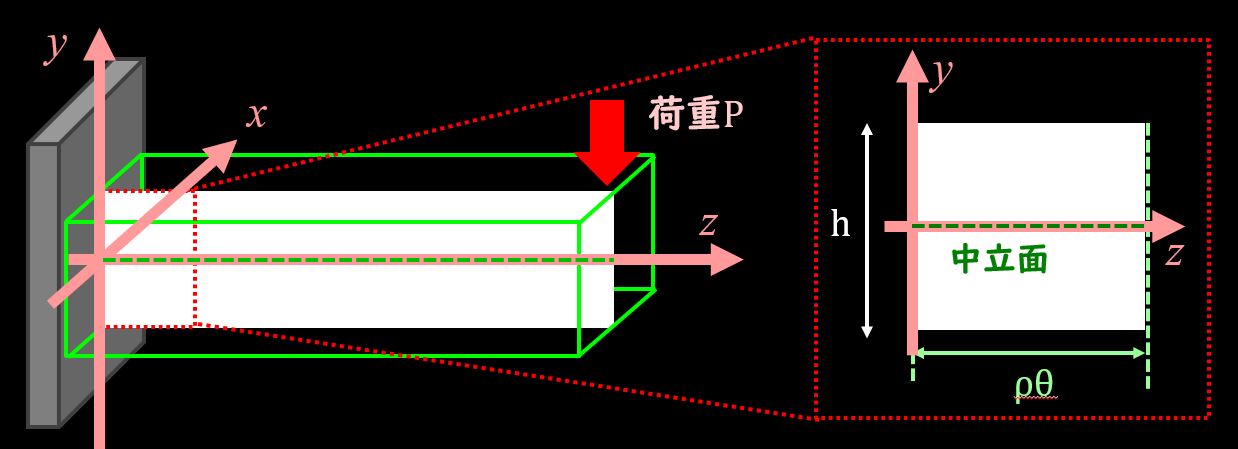
それでは2つの前提条件を踏まえて、曲げ応力の詳細を見ていきましょう。
片持ち梁を用意し、曲げ応力が最大となる、固定部に着目しましょう。
片持ちはりの固定部に1番大きな曲げ応力、曲げモーメントが発生することは過去の記事で解説していますので、参考にしていただければと思います。
もともと曲がっていない状態から梁を曲げると、断面の関係性がどのようになるか見ていきましょう。
中立軸は応力がゼロとなるラインなので、右側の面の中立軸部分は、曲げても変位しないことになります。
つまり中立軸を中心に面が少し傾くことになりますね。
このような状態になった時、左側の面と、右側の面のなす角を曲率\(θ\)と呼び、下図のように交点と中立軸までの距離を曲率半径\(ρ\)と呼んでいます。
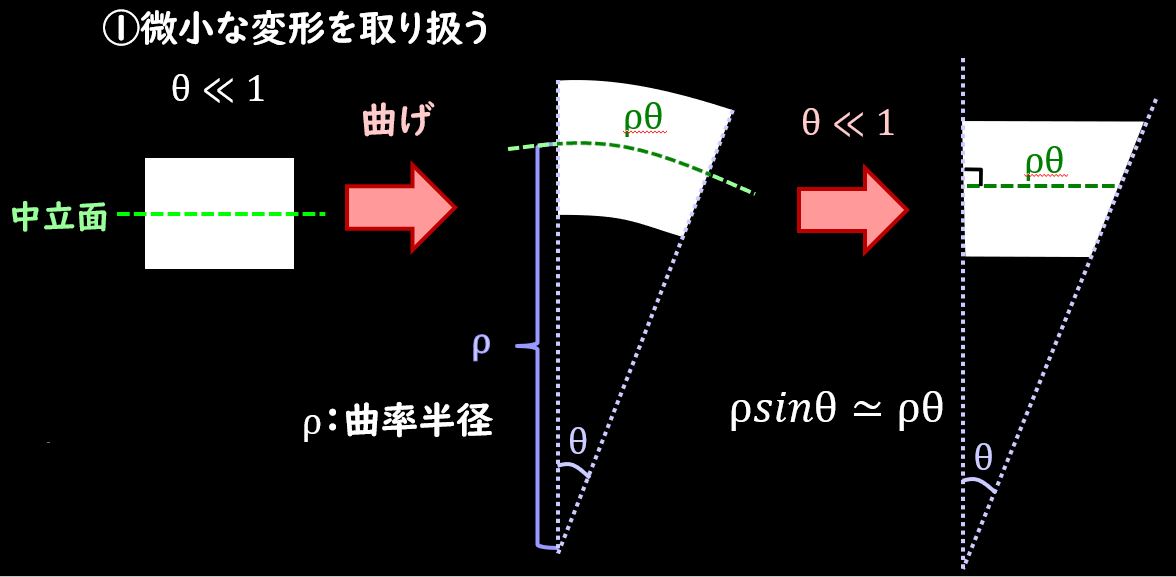
そして、ポイントとして、このときの\(θ\)が非常に小さいとします。
\(θ\)が非常に小さいとすると、左側の面と右側の面を繋いでいる弧の長さと、左側の面から垂直に右側の面との距離をとった長さが等しくなります。
これは前提条件のところで説明させていただいたように、三角関数の近似を用いるとこのようになりますね。
この梁の様子を注意深く見てみると、梁の上側は伸びており、梁の下側は縮んでいるように見えますね。
この各場所での変形量が曲げ応力の原因になっています。
材料力学では変形量をひずみとして表すのでしたね。
中立軸をz軸、中立軸に垂直な方向にy軸をとると、とある\(y\)でのひずみ量は図形的に下記のようになりますね。
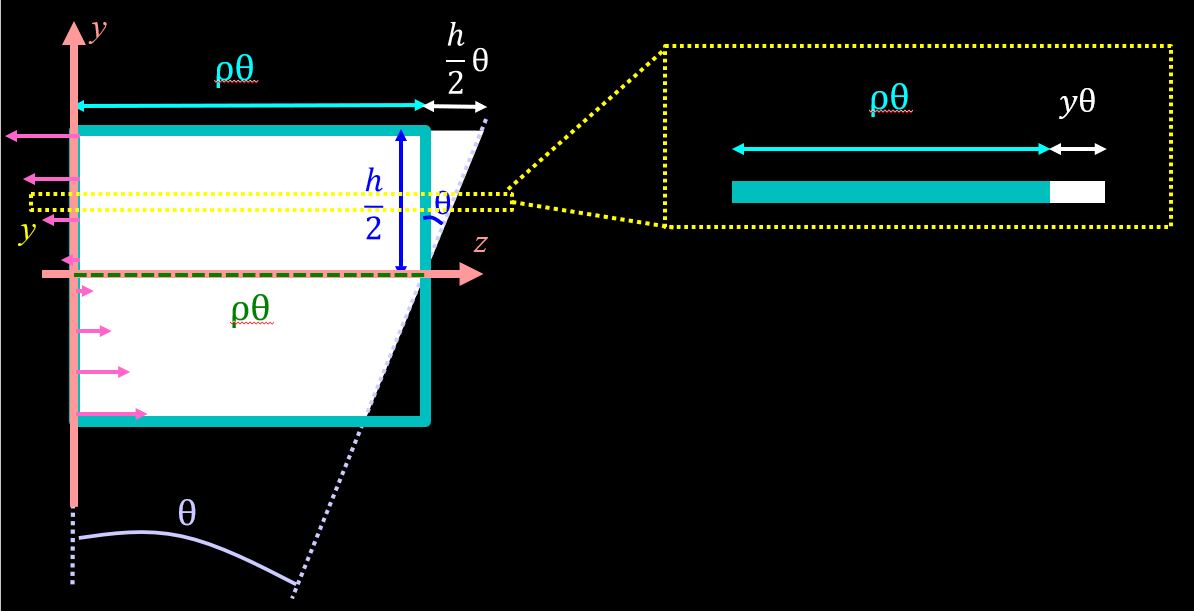
$$ε=\frac{yθ}{ρθ}=\frac{y}{ρ}$$
このように、\(y\)軸方向に1次関数的にひずみが増大することになります。
ひずみと応力の関係はフックの法則で表すことができますので、フックの法則は\(σ=Eε\)であるから、
$$σ(y)=E\frac{y}{ρ}$$
と表すことができます。
この\(σ(y)\)がとあるy座標での曲げ応力を表しており、これもひずみと同様に\(y\)軸に対して1次関数的に変化しています。
よって、下図のような応力分布になるわけです。
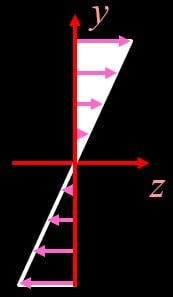
もっとよりイメージしやすくするために
梁をバネで置き換えてみましょう。
下図のような形ですね。
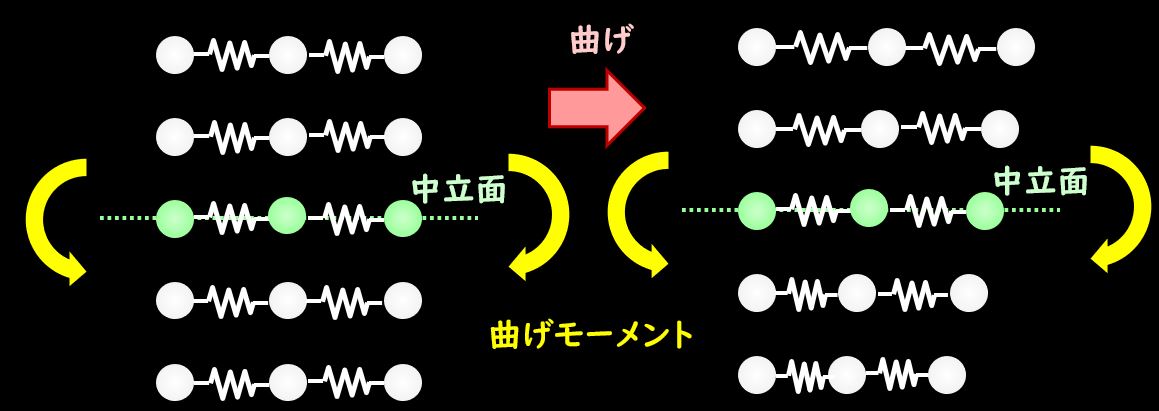
バネの力もフックの法則で表すことができますね。
このようにバネで表すことで、三角形の分布になることが理解しやすくなるのではないでしょうか?
まとめ
本日は曲げ応力が三角形の分布になることを解説しました。
前提となる下記の2つの条件をしっかりと抑えた上で、フックの法則を使えば理解することができます。
ポイント
- 微小な変形を取り扱っている
- オイラーベルヌーイの梁を家仮定
あとは梁をバネに変えてイメージを持っていただくとすんなりと理解できるのではと思います。
初心者向けの教科書・参考書はこちら
材料力学の記事一覧はこちら
次の記事 → 曲率半径から曲げの式を導出する 曲率半径と曲率をしっかりとイメージしよう!
