連成振動の一般解ってモード解析法を使わないと結局解けないの?


質量とバネ定数が同じの簡単なモデルであれば解くことはできるから、今日はモード解析法を使わずに解いてみよう。
今回は連成振動の一般解をモード解析法を使わずに解いていきます。
減衰無しで質量、バネ定数が同じであれば、いくつかの解の仮定を使うことで解くことができますので、解法の流れを理解しましょう。
モード解析法については過去の記事で解説していますので、参考にしていただければと思います。
過去記事
また、動画でも解説しておりますので、こちらも是非参考にしていただければと思います。
モデル

今回取り扱うモデルは上図のようなモデルになります。
N個の質点がバネで繋がっているようなモデルで、質量とバネ定数が全て同じ状態です。
運動方程式
さて、運動方程式を立てましょう。
運動方程式の立て方についての詳細は過去の記事で解説していますので、そちらを参考にして頂ければと思います。
とある\(i\)番目の運動方程式を立てると下記のようになります。
このi番目の運動方程式を解いて、解がわかれば1番目の質点も2番目の質点も、 \(i=1\)や\(i=2\)とすることで解がわかることになりますね。
解の仮定
それでは一般解を求めるために、下記の3点を仮定します。
え?なんでかって?
そうやるとうまくいきそうだからです。
ポイント
- 解は時間的に三角関数で表すことができる
- 解は空間的にも三角関数で表すことができる
- 解は上記の仮定を満たしたうえで、線形結合で表すことができる
はい、どういうこと~?っていう声が聞こえてきそうなので、1つずつ説明していきますね。
①時間的に三角関数で表せる
これはこれまでの1自由度や2自由度で勉強した通り、解を\(sinωt\)や\(cosωt\)で表してきたことと同じです。
振幅を\(A\)、固有振動数を\(ω\)とすると、特殊解として、
$$x_n=u_nsin(ωt+Φ)$$
と表すことができる、ということですね。
で、この仮定自体は1自由度でも2自由度でも成り立っていましたので、今回も成り立つ、という前提で進めちゃいましょうということです。
②空間的に三角関数で表せる
これは1自由度や2自由度では出てこなかった概念ですね。
アニメーションを見て頂いた方が理解しやすいと思いますので、下記のアニメーションをご覧ください。

各質点が揺れるときに、\(sin\)カーブになっていますね?
そう、各質点の振幅が\(sin\)とか\(cos\)の波形で表せますよ、という仮定をいれるのです。
振幅\(A_n\)を下記のように表します。
$$u_n=Asin(pn+θ)$$
運動方程式を解く
それでは運動方程式に特殊解を代入して、一般解を求めましょう。
\(n\)番目の質点の運動方程式は、
まずこの式に下記の特殊解を代入します。
$$x_n=u_nsin(ωt+Φ)$$
代入すると、
両辺を\(cos(ωt+Φ)\)で割ると
次に振幅の形も下記のように仮定しておりましたので、代入しましょう。
$$u_n=Asin(pn+θ)$$
これを代入すると、
三角関数の和積の公式を使って、
$$-mω^2Asin(pn+θ)=-Ak(2sin(pn+θ)-2cosp・sin(pn+θ))$$
さらに三角関数の半角の公式を使って整理すると、
$$-mω^2Asin(pn+θ)=-Ak(2-2cosp)sin(pn+θ))$$
両辺を\(Asin(pn+θ)\)で割ると
$$mω^2=k(2-2cosp)$$
よって、\(ω\)は
$$ω_m=2\sqrt{\frac{k}{m}}sin\frac{p}{2}$$
となって、この\(ω\)の時、解として成立し、\(ω\)が固有振動数となります。
次に\(θ\)の値を決定するために、境界条件を見てみます。
\(u_0\)と\(u_{N+1}\)の値を考えると、下記の図の黄色枠部に相当します。
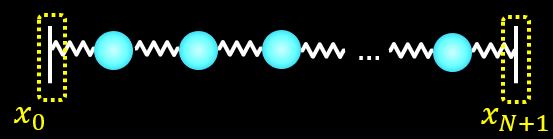
黄色枠部は固定端に相当するので、常にゼロとなります。
よって、
$$u_0=Asinθ=0$$ つまり、\(θ=0 or π\)となり、今回は\(θ=0\)を採用します。
ちなみに\(θ=π\)でも\(A\)の符号を逆にすればOKです。
つぎに\(u_{N+1}\)についてですが、
$$u_{N+1}=Asin(p(N+1)+θ)=0$$
となりますので、
$$p(N+1)=mπ$$
\(p\)の値は
$$p_m=\frac{m}{N+1}π$$
となるので、固有振動数\(ω\)は、
このときの振幅を求めると、
$$u_n=Asinp_mn=Asin\frac{m}{N+1}πn$$
よって、
$$x_n=u_ncos(ω_nt+Φ_n)$$
一般解はモードの重ね合わせだから
未知数は\(ω_m,Φ_m\)の2N個になり、一般解の形が求まります。
まとめ
N個の連立微分方程式の一般解について解説しました。
$$x_n=\sum^N_{m=1}u_msinp_mn・cos(ω_mt+Φ_m)$$
減衰が無く、バネ定数、質量が同じ場合、時間的にも空間的にも三角関数の形で表すことができる、 という仮定を用いることで、一般解を求めることができます。
ポイント
- 解は時間的に三角関数で表すことができる
- 解は空間的にも三角関数で表すことができる
- 解は上記の仮定を満たしたうえで、線形結合で表すことができる
初心者向けの教科書・参考書はこちら
振動工学の記事一覧はこちら
次の記事 →振動・波動の基礎-㉓連続体の振動の運動方程式-波動方程式の導出
