連続体の振動の分野って、これまでやってきた多自由度の振動と違って、微分とかがすごく複雑でわかんないだけど…


連続体の分野はモデルの立て方とか考え方が変わってくるけど、理解できるように丁寧に解説するね。
本日は連続体の振動の基礎として、モデルと運動方程式の立て方について解説します。
材料力学でも学ぶ内容ですが、初めて学ぶ方でも理解できるように、丁寧に解説していきますね。
連続体に近い系として、多自由度の振動も過去に解説していますので、参考にしてください。
参考記事
本記事をおススメする人
連続体の振動を勉強している人
物理を勉強していて興味がある人、仕事で振動の知識を使う人
今回は簡単な例として、弦の振動について考えていきます。
また、動画でも解説していますので、こちらも是非参考にしていただければと思います。
連続体のモデル
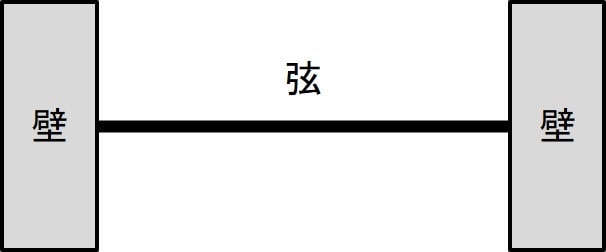
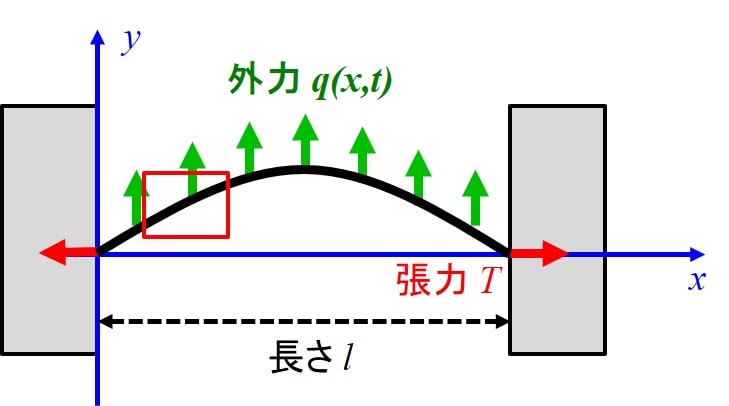
上記のように連続体として両端を固定した弦を考えます。
この弦がピンっと張ったときと平行な方向を\(x\)軸、\(x\)軸と垂直な方向を\(y\)軸とします。
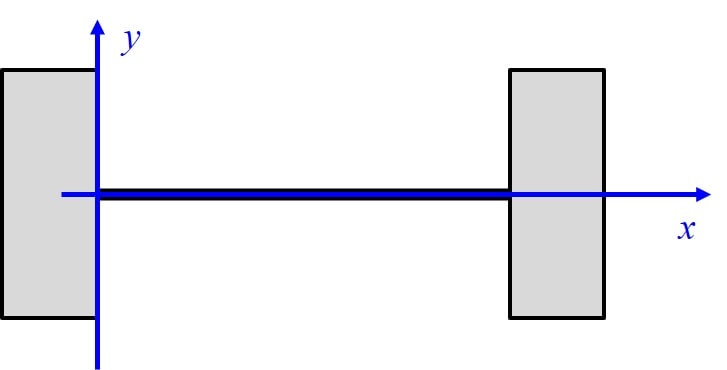
この弦についてのパラメータとして、下記を定義します。
\(l\):長さ \(μ\):線密度 \(T\):張力
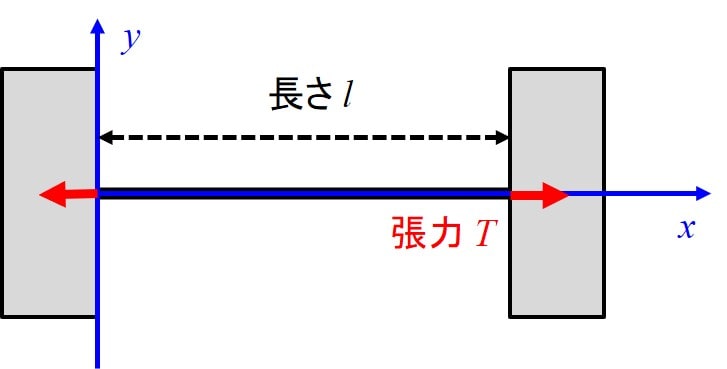
この弦に下図のように単位長さ当たり\(q(x,t)\)の強制力を作用させることを考え、 \(y(x,t)\)をとある\(x\)座標の弦のたわみ量とします。
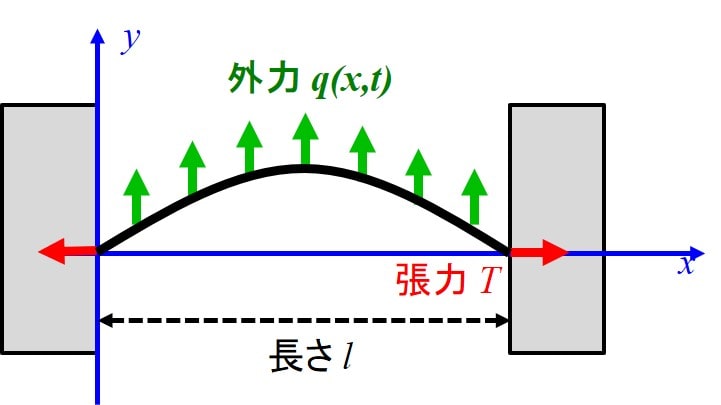
運動方程式の立て方
弦の中からとある位置の微小領域を抜取り、運動方程式を考えます。
上記の赤枠部分を拡大したのが下図になります。
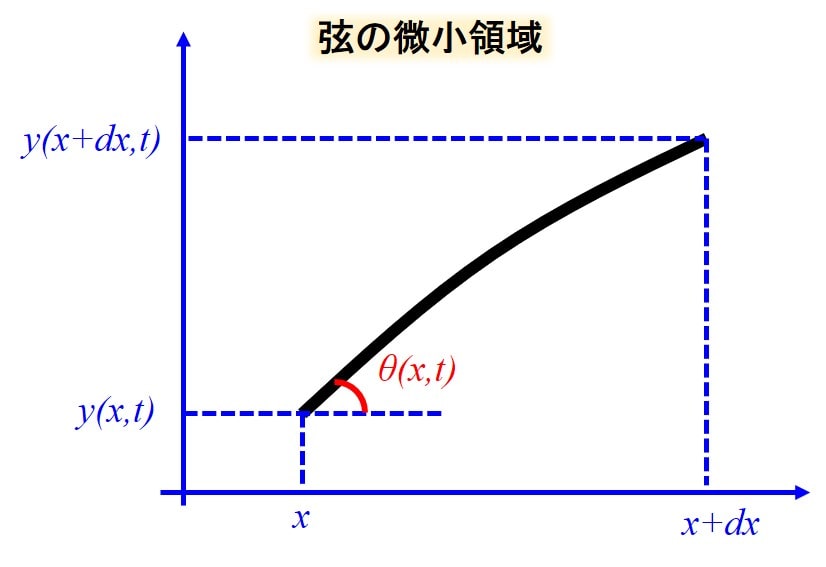
微小領域の左端のx軸とのなす角を\(θ(x,t)\)とします。
θが微小である\((θ<<1)\)と仮定すると、\(tanθ≒θ\)と近似することができ、傾きが\(θ\)となって下記のような関係式が成り立ちます。
$$θ=\frac{\partial y(x,t)}{\partial x}$$
ここから運動方程式\(ma=F\)の形にもっていきましょう。
まず質量\(m\)について、線密度が\(μ\)で、微小領域の長さがdxなので、 $$m=μdx$$ となりますね。
次に加速度\(a\)については、弦の動く方向は\(y\)軸方向ですので、\(y\)軸方向の加速度として、
$$a=\ddot{y}(x,t)$$
弦に生じている力に関しては、詳しく見ていきましょう。
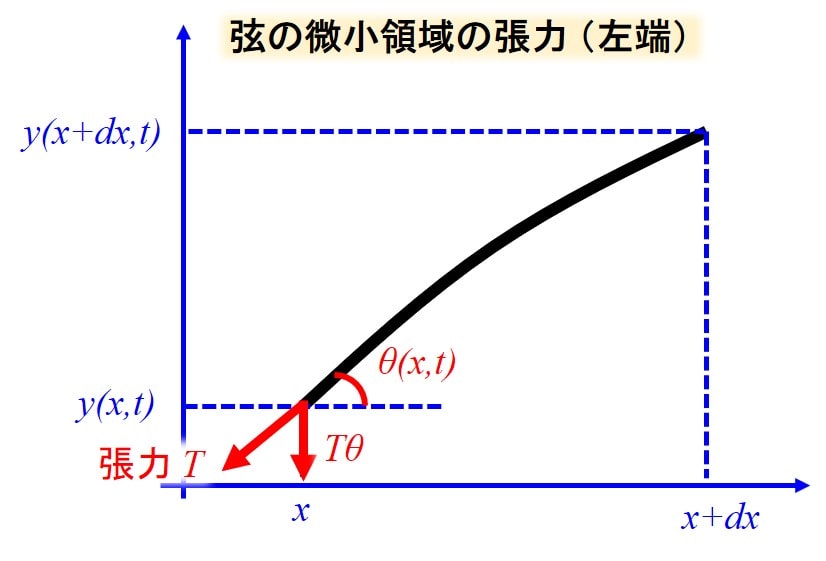
微小領域の弦の両端に発生している力を考えると、左端側は\(-Tsinθ\)とあらわすことができますね。
ここで、\(θ<<1\)とすると\(sinθ≒θ\)と近似できますので、\(-Tθ\)となります。
次に右端側については下記のようになります。
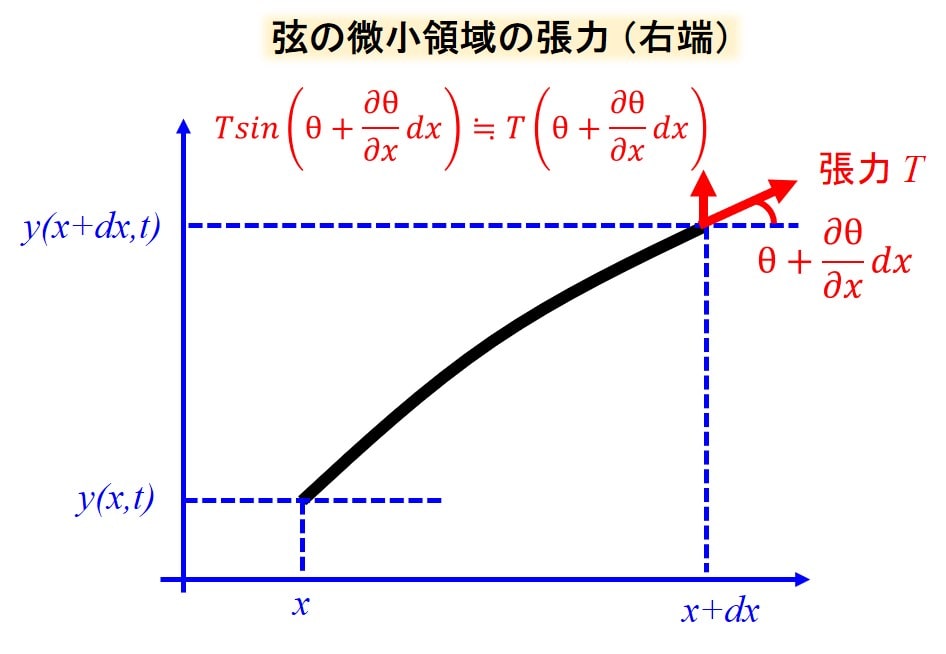
$$T(θ+\frac{\partial θ}{\partial x})dx$$
さらに外力\(q(x,t)\)の強制力が単位長さにかかっていますので、力\(F\)は
整理すると、
この式に下記を代入します。
$$θ=\frac{\partial y(x,t)}{\partial x}$$
すると、
$$F=T\frac{\partial^2 y}{\partial x^2}dx+q(x,t)dx$$
よって運動方程式は、
両辺を\(μdx\)で割ると、
強制力がない場合は、
この方程式は波動方程式と呼ばれ、棒の縦振動、ねじり振動、音の伝搬などもこの方程式に従います。
この波動方程式を見てみると、変位yは位置xと時間tの2変数関数となっているので、 微分方程式としては偏微分方程式となっています。
この運動方程式が連続体の運動を記述するための基礎となりますので、しっかりと理解しておきましょう。
まとめ
今回は連続体の運動方程式から、波動方程式の導出を行いました。
作り方としては、とある微小領域をもってきて、力を書き出して運動方程式を作る、というやり方となります。
波動方程式は位置と時間の関数となることに注意です。 これが基礎となりますので、しっかりと考え方をマスターしておきましょう。
参考文献
- 振動工学の基礎:岩壺卓三、松久寛、森北出版株式会社
- 機械力学-振動の基礎から制御まで:日高照晃、小田哲、川辺尚志、曽我部雄次、吉田和信、朝倉書店
- 構造と連続体の力学基礎:熊でもわかる変形できる物体の力学:岩熊哲夫、小山茂 web版
初心者向けの振動工学の教科書・参考書をこちらで紹介していますので、参考にしていただければと思います。
初心者向けの教科書・参考書はこちら
振動工学の記事一覧はこちら
次の記事 → 振動・波動の基礎-㉔連続体の振動 運動方程式と自由振動の一般解をわかりやすく解説
