固有値とか固有ベクトルっていうのがでてきたんだけど、全然イメージつかないです…


固有値は非常によく使う線形代数の知識だから、詳しく解説するね。
本日は固有値、固有ベクトルについて解説します。
これらを解説する前に、前提として行列とベクトルの掛け算の話が出てきますので、 線形変換が理解できていない方は、過去の記事を参考にして頂ければと思います。
固有値と固有ベクトル
線形変換の復習
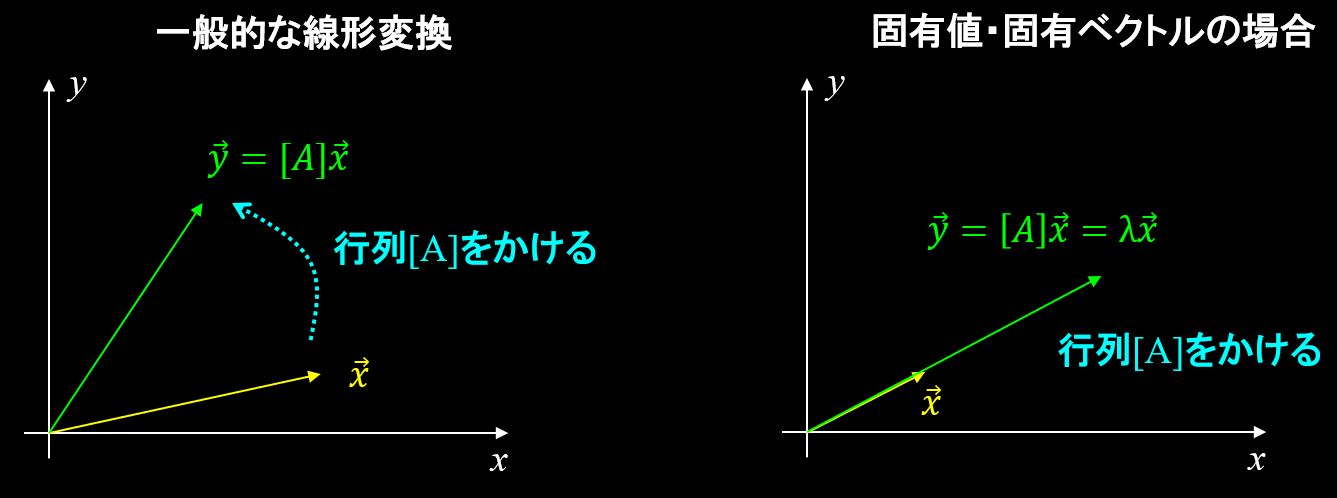
行列×ベクトルを行って、別のベクトルに変換することを 線形変換と呼びます。
こちらは過去の記事でも参考にしてください。
例えば、ベクトル\(\vec{x}\)に行列[A]をかけてあげて、ベクトル\(\vec{y}\)に変換したとすると、下記のように表されます。
$$[A]\vec{x}=\vec{y}$$
固有値と固有ベクトルは、この線形変換のある特定の場合に出てくるもので、
$$\vec{y}=λ\vec{x}$$
と書ける場合に、λを固有値、\(\vec{x}\)を固有ベクトルと呼びます。
教科書とかには
$$[A]\vec{x}=λ\vec{x}$$
という風に書かれています。
どういうこと?って思ったかもしれませんので、
イメージを文章で書いておくと、
ベクトルに行列をかけたときに、向きが変わらず長さだけが定数倍されるような線形変換の場合、 そのベクトルを固有ベクトル、長さの倍率を固有値、と呼んでいるのです。
固有値と固有ベクトルは、その性質上、必ずセットで出てきます。
図で書くと下記のような形ですね。
具体例
通常の線形変換
$$\left(\begin{array}{cc}3&1\\2&2\end{array}\right)\left(\begin{array}{c}1\\2\end{array}\right)=\left(\begin{array}{c}5\\6\end{array}\right)$$
変換前のベクトルと変換後のベクトルを見てみると、下図のように向きが変わっていますね。

固有値・固有ベクトルの場合
$$\begin{eqnarray}\left(\begin{array}{cc}3&1\\2&2\end{array}\right)\left(\begin{array}{c}1\\1\end{array}\right)&=&\left(\begin{array}{c}4\\4\end{array}\right)\\&=&4\left(\begin{array}{c}1\\1\end{array}\right)\end{eqnarray}$$
こちらの場合、変換前と変換後のベクトルは向きは同じで長さが変わっているのがわかります。

固有値と固有ベクトルの求め方
じゃあこの固有値と固有ベクトルってどういう風にもとめたらいいの?


固有方程式というものがあるから、それを解くことになるね。
行列\([A]\)と固有ベクトル\(\vec{x}\)、固有値λを式で表すと、
$$[A]\vec{x}=λ\vec{x}$$
これを左辺にまとめると
$$[A]\vec{x}-λ\vec{x}=0$$
\(\vec{x}\)でくくると
$$([A]-λ[E])\vec{x}=0$$
この式において、\(\vec{x}=0\)以外に\(\vec{x}\)が存在する必要があるので、
$$|[A]-λ[E]|=0$$
と行列式がゼロである必要があります。
行列式がゼロでない場合、逆行列が存在することになり、逆行列を左からかけると
$$\vec{x}=0$$
となってしまいます。
この行列式を解くことで、固有値を求めることができ、求まった固有値を固有方程式に代入することで、固有ベクトルが求まります。
こちらは過去の記事でも解説していますので、参考にしてください。
具体例
下記の2行2列の行列の固有値、固有ベクトルを求めてみましょう。
$$[A]=\left(\begin{array}{cc}3&1\\2&2\end{array}\right)$$
固有値をλ、固有ベクトルを\(\vec{x}\)とすると、
$$[A]\vec{x}=λ\vec{x}$$
となるから、
$$([A]-λ[E])\vec{x}=0$$
となって、
$$|[A]-λ[E]|=0$$
となる必要があるわけですね。
左辺を計算すると、
$$\left|\begin{array}{cc}3-λ&1\\2&2-λ\end{array}\right|=0$$
行列式を計算すると
$$(3-λ)(2-λ)-1×2=λ^2-5λ+4$$
この二次方程式を解くと、
$$(λ-4)(λ-1)=0$$
となって\(λ=1,4\)となります。
この2つ出てきた固有値に対してそれぞれ固有ベクトルが存在することになります。
\(λ=1\)のとき 固有ベクトルを下記のように置きます。
$$\vec{x}=\left(\begin{array}{c}x_1\\x_2\end{array}\right)$$
よって、\(([A]-λ[E])\vec{x}=0\)なので、
$$\left(\begin{array}{cc}3-1&1\\2&2-1\end{array}\right)\left(\begin{array}{c}x_1\\x_2\end{array}\right)=0$$
これを計算すると下記の方程式を得ます。
$$2x_1+x_2=0$$ $$2x_1+x_2=0$$
同じ形の方程式が出てきましたね。
列式がゼロになってしまうので、固有ベクトルは一意に決まりません(比のみが求まります)
$$x_2=-2x_1$$
となります。
λ=4のとき
$$\left(\begin{array}{cc}3-4&1\\2&2-4\end{array}\right)\left(\begin{array}{c}x_1\\x_2\end{array}\right)=0$$
同様に計算すると
$$-x_1+x_2=0$$ $$2x_1-2x_2=0$$
これも同じ形の方程式となってしまって、
$$x_1=x_2$$ と比のみが求まります。
このように固有ベクトルは比のみが求まる形になります。
物理分野への応用
振動工学の分野では、モード解析法や、多自由度系の振動についての運動方程式を解くときに、固有値・固有ベクトルの知識を使います。
下記の動画で、モード解析法の解説をしていますが、固有値、固有ベクトルの概念をベースに進めていますので、応用例を知りたい方は是非参考にしていただければと思います。
まとめ
固有値と固有ベクトルについて解説しました。
固有値、固有ベクトルは下記のように出てきて、固有値、固有ベクトルはセットになっています。
$$[A]\vec{x}=λ\vec{x}$$
行列\([A]\)に対する固有ベクトル$\vec{x}$を掛けた場合、向きが変わらず、長さだけ定数倍される形になります。
固有値を求める場合は、下記の固有方程式を解けばよく、固有ベクトルは比の形で求まります。
$$|[A]-λ[E]|=0$$
固有値、固有ベクトルは物理のあらゆる分野で顔を出す数学なので、この一連の流れを必ず頭に入れておきましょう。
