単振り子の動きも単振動なの?


そうだよ、振り子も何パターンかあるので、解説するね。
本日は振り子について解説します。

単振動の例としてよく取り扱われるので、しっかり理解しておきましょう。
今回は下記のようなモデルを取り扱います。
- 単振り子
- 段差のある振り子
- 剛体振り子
バネモデルの1自由度の振動については下記の過去の記事を参考にして頂ければと思います。
単振り子のモデルと運動方程式
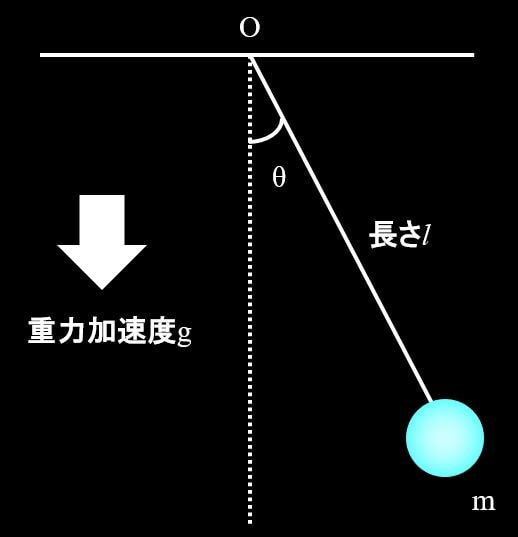
上図のように振り子の長さを\(l\)、おもりの重量を\(m\)、重力加速度を\(g\)とします。
単振り子の支点を\(O\)として、下図のように角度を\(θ\)とし、簡単のために\(θ\)は微小角度とします。
\(θ\)方向に運動方程式を立てることを考えると、
$$ml^2\ddot{θ}+mglsinθ=0$$
となります。
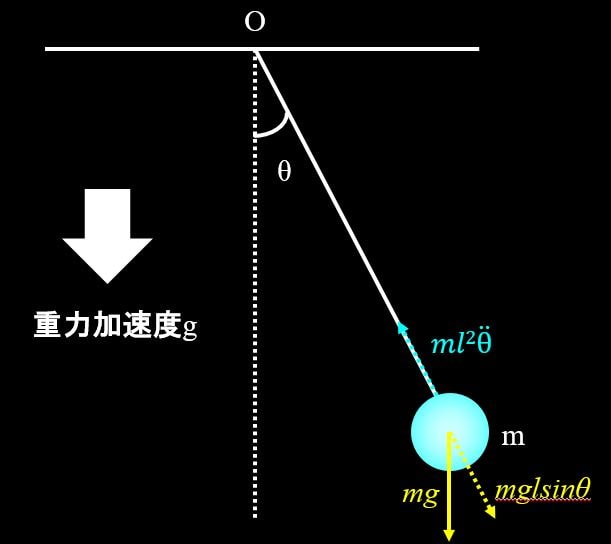
θは微小な角度なので$θ<<1$より$sinθ≒θ$となって、
$$\ddot{θ}+ω_n^2θ=0$$
$$ω_n=\sqrt{\frac{g}{l}}$$
このように単振動と同じ形で表すことができます。
段差のある振り子
それでは下図のような振り子を考えてみましょう。
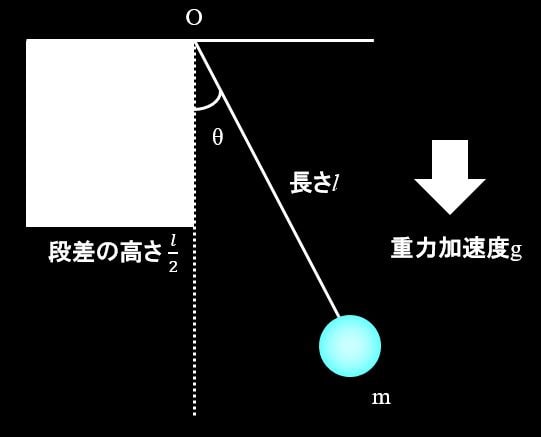
\(θ=α\)の位置までおもりを移動させ、そこから静かに手を離したとします。
このとき、どのくらいの角度まで移動するかを調べます。
まず、長さ\(l\)の振り子の周期\(T\)は
$$T=\frac{2π}{ω}=2π\sqrt{\frac{l}{g}}$$
初期変位\(θ=α\)で静かにはなしたときのおもりの運動は
$$θ(t)=αcos(t\sqrt{\frac{g}{l}})$$
平衡点を通過するときの角速度は
$$\dot{θ}=-α\sqrt{\frac{g}{l}}$$
とあらわすことができるので、速度は\(l\dot{θ}=-α\sqrt{gl}\)となります。
この値が初期速度として考えて、長さが\(\frac{l}{2}\)の振り子の運動は、
$$θ(t)=-\sqrt{2}αsin(t\sqrt{\frac{2g}{l}})$$
となります。
剛体振り子
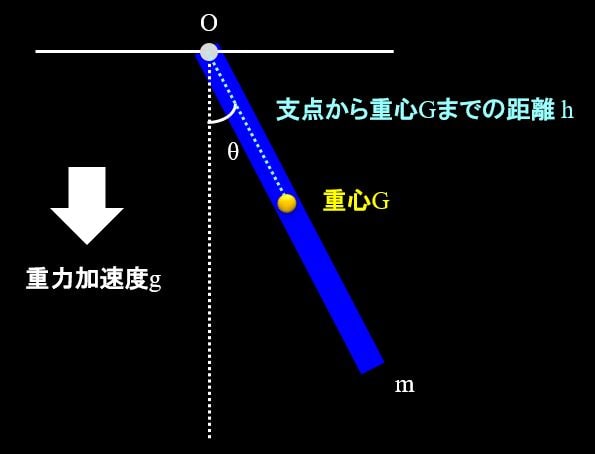
固定点\(O\)周りの剛体の運動は、慣性モーメントと復元モーメントがつり合います。
慣性モーメントは
$$I\ddot{θ}、(I=I_d+mh^2)$$
ここで\(I_d\)は重心回りの慣性モーメントで、\(h\)は重心と支点の距離を示します。
復元モーメント\(M\)は
$$M=-mghsinθ$$
ここで、\(sinθ≒θ\)と近似すると、
$$M=-mghθ$$
慣性モーメントと復元モーメントがつりあうので、\(I\ddot{θ}=M\)となり、
$$I\ddot{θ}+mghθ=0$$
両辺を\(I\)で割ると、
$$\ddot{θ}+\frac{mgh}{I}θ=0$$
\(θ\)の係数を\(ω_n^2\)と置くと、
$$\ddot{θ}+ω_n^2θ=0$$
$$ω_n=\sqrt{\frac{mgh}{I}}$$
このように、単振動の運動方程式と同じ形の微分方程式となります。
剛体振り子の固有振動数は\(ω_n\)となります。
まとめ
今回は単振り子、段差のある振り子、剛体振り子について解説しました。
振り子にもいろんなパターンがありますので、是非いろんな問題を解いて、慣れていってくださいね。
初心者向けの教科書・参考書はこちら
振動工学の記事一覧はこちら
