縦振動の運動方程式が両端固定の弦と同じことなのはわかったんだけど一般解の形って具体的にどうなるの?


両端固定の弦の場合は、弦が上下にゆれるような振動になるけど、棒の縦振動の場合、伸び縮みする方向の振動だから、見た目は少し変わるんだ。 でも両端固定の弦と基本的に同じ動きになっているから、今回は具体例を見てしっかりとイメージできるようにしよう。
今回は棒の縦振動の具体例について解説します。
縦振動の運動方程式や両端固定の弦については過去の記事で解説していますので、参考にしてください。
過去記事
下記の動画でも解説していますので、是非参考にしていただければと思います。
モデルと運動方程式
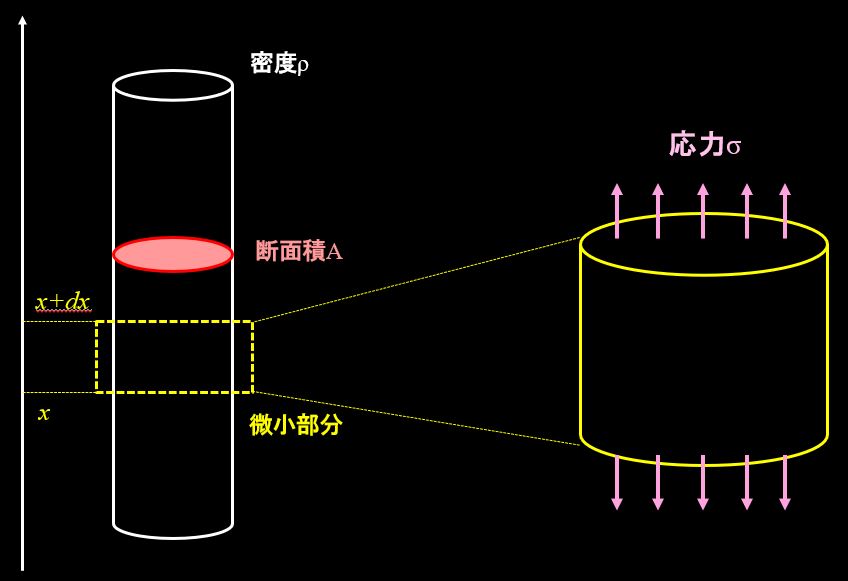
上図のように、密度が\(ρ\)の縦長の棒を用意し、棒の中の微小部分を取り出して考えます。
棒の断面積\(A(x)\)、棒の下端を\(x\)、棒の上端を\(x+dx\)とし、振動することによって断面部分に発生する応力をσとします。
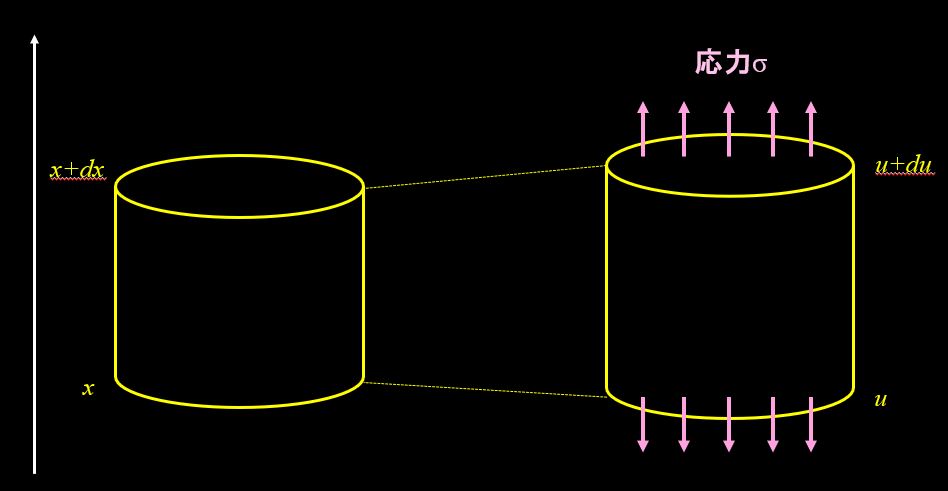
この微小部分に応力\(σ\)が発生したときの、棒の変位を\(u\)とし、フックの法則から応力とひずみは下記になります。
$$σ=Eε=E\frac{\partial u(x,t)}{\partial x}$$
\(ε\)はひずみ、\(E\)は縦弾性係数(ヤング率)です。
これらを用いると運動方程式は
$$\frac{\partial^2u}{\partial t^2}=c^2\frac{\partial^2u}{\partial x^2}$$ $$c=\sqrt{\frac{E}{ρ}}$$
一般解
この運動方程式から解を求めるには、両端固定の弦と同じように、変数分離法を用います。
運動方程式の解を $$u(x,t)=Y(x)G(t)$$ と位置の関数\(Y(x)\)と時間の関数\(G(x)\)の積で表します。
この解き方は過去の記事を参考にして頂くとして、結果を下記に示します。
$$Y(x)=Acoskx+Bsinkx$$ $$G(t)=Ccosωt+Dsinωt$$
ただし\(k=\frac{ω}{c}\)です。
これらの係数\(A、B、C、D\)を初期条件や境界条件から求めることになります。
一般解は全ての次数の固有振動モードの足し合わせで表すことができますが、 簡単のために変数分離した解の形を用いて具体例を考えましょう。
具体例 一端固定棒
上図のように棒の片側を固定、もう片方を自由な状態にしたときの振動モードを考えましょう。
境界条件として、固定されている部分\((x=0)\)の部分では、変位が常にゼロとなるので、 $$u(0,t)=0$$ となります。
この条件から、
$$u(0,t)=Y(0)G(t)=0$$
となり、\(Y(0)=0\)となります。 \(Y(x)=Acoskx+Bsinkx\)なので、\(x=0\)のとき、
$$Y(0)=A=0$$
となり、\(A\)が求まります。 次に固定していない側の自由端\((x=l)\)では、応力が解放されていて\(σ=0\)となります。
応力とひずみの関係式はフックの法則から導出され、
$$σ=Eε=E\frac{\partial u(l,t)}{\partial x}=0$$
となります。
この式にも\(Y(x)とG(t)\)を入れると、
$$σ=E\frac{\partial Y(x)G(t)}{\partial x}_{x=l}=0$$
\(G(t)\)は位置の微分には関与しないので、
$$σ=EG(t)\frac{\partial Y(x)}{\partial x}_{x=l}=0$$
\(Y(x)\)を微分すると
$$\frac{dY}{dx}=-Asinkx+Bcoskx$$
この微分して\(x=l\)を代入したものがゼロとなるので、\(A=0\)であることに注意すると
$$coskl=0$$
となります。
よって、
$$k_n=\frac{(2n-1)π}{2l}$$
ただし\(k=\frac{ω}{c}\)ですので、固有振動数\(ω_n\)は
$$ω_n=ck_n=\frac{(2n-1)π}{2l}\sqrt{\frac{E}{ρ}}$$
\(c=\sqrt{E}{ρ}\)です。
一般解は\(n=1,2,3…\)のすべての次数の固有振動モードの波形を足し合わせたものになりますが、 簡単のために1次の固有振動モードについて、見てみましょう。
具体例を確認
1次の固有振動モードを見たいので、\(n=1\)とすれば、\(Y(x)\)は下記のようになります。 $$Y_1(x)=Bsin\frac{π}{2l}x$$
係数\(B\)と\(G(t)\)を求める必要があるので、初期条件として\(G(0)=0\)、\(\dot{G}(0)=v_0\)とすると、
$$G(0)=C=0$$
$$\dot{G}(0)=Dω=v_0$$
よって、
$$G(t)=\frac{v_0}{ω}sinωt$$
1次の固有振動の解は
$$u_1(x,t)=Bsin\frac{π}{2l}x・\frac{v_0}{ω_1}sinω_1t$$
\(B\)は未定係数なので、仮に1として、棒を8分割した点の動きを示すと、下記のようなグラフになります。
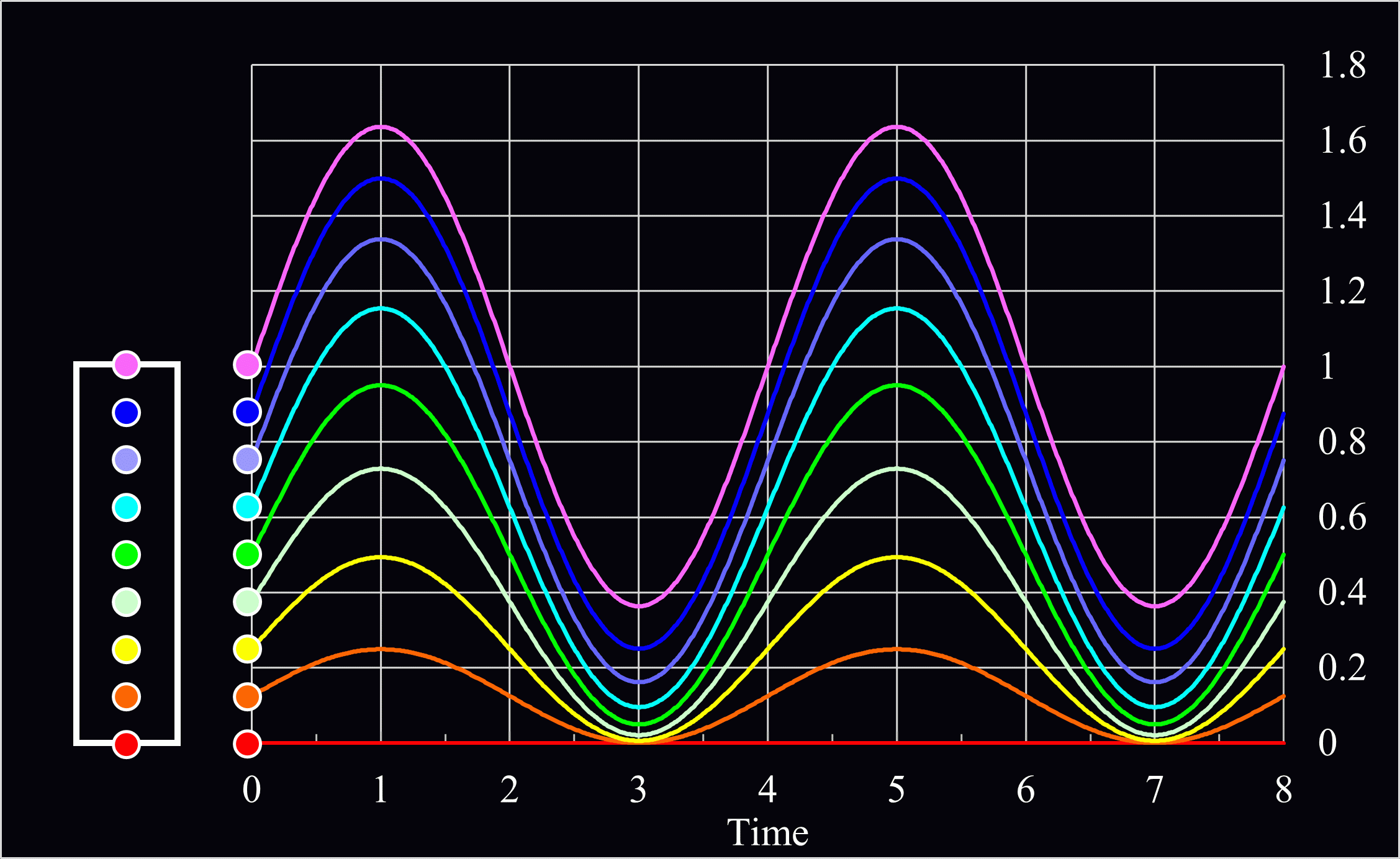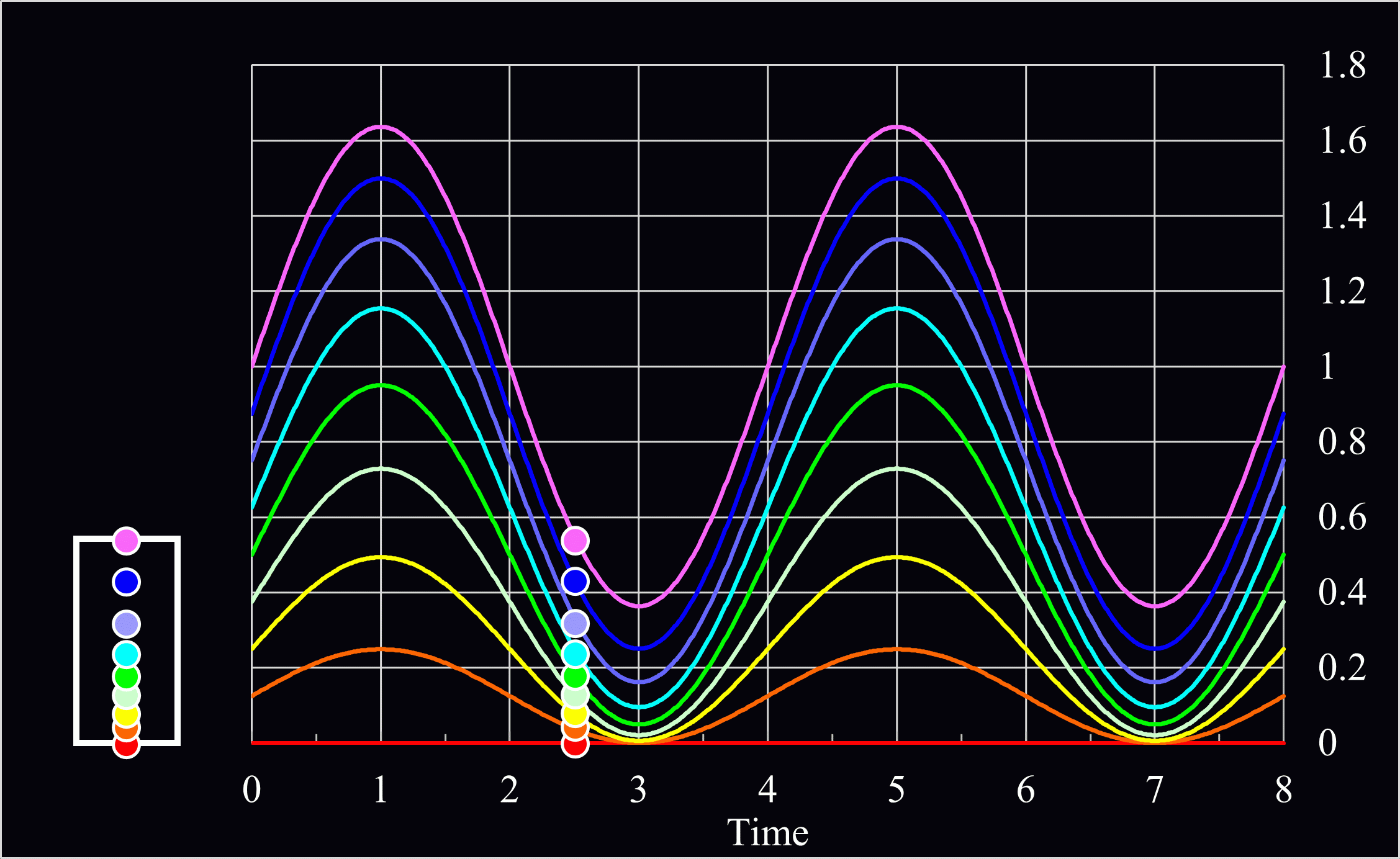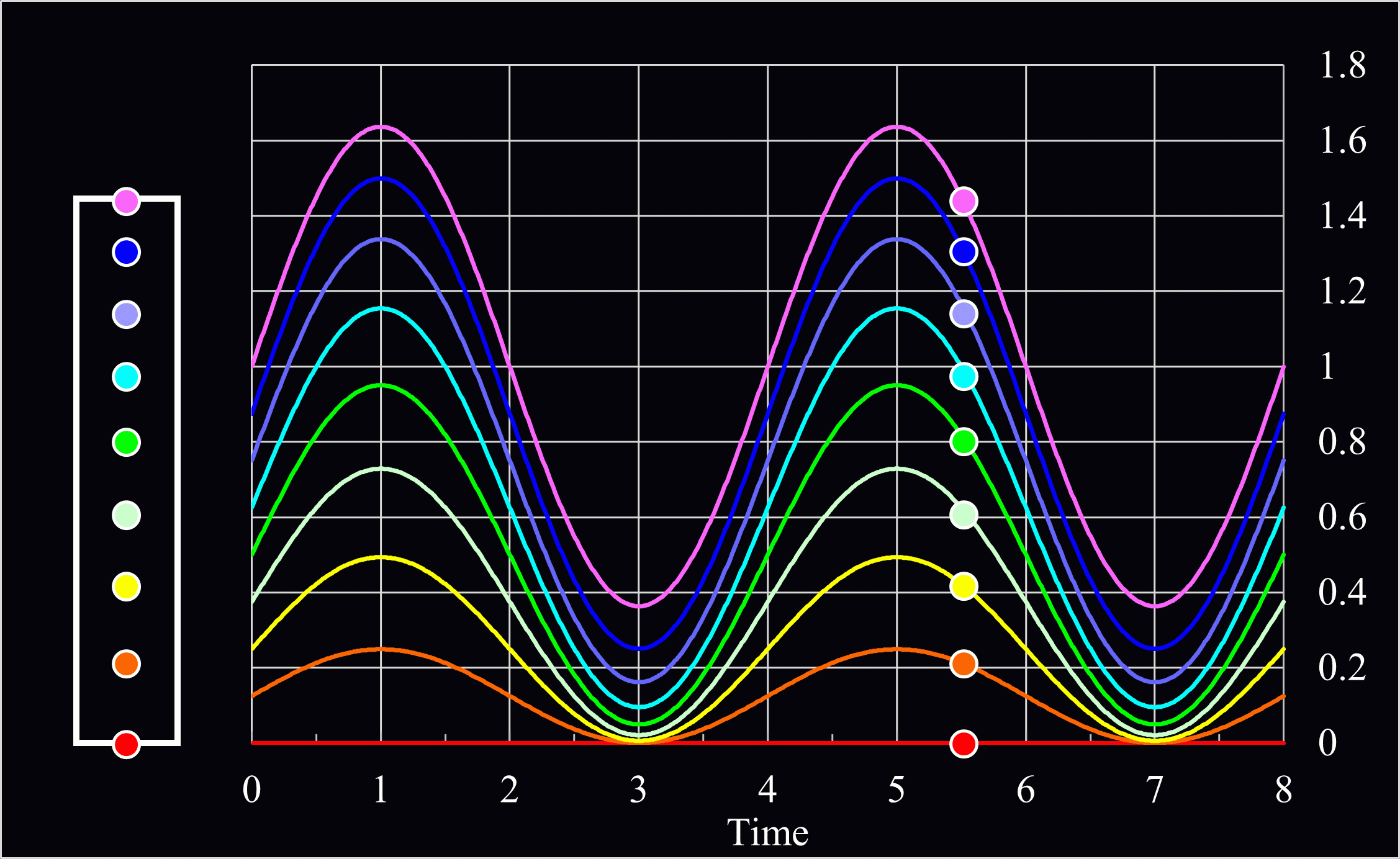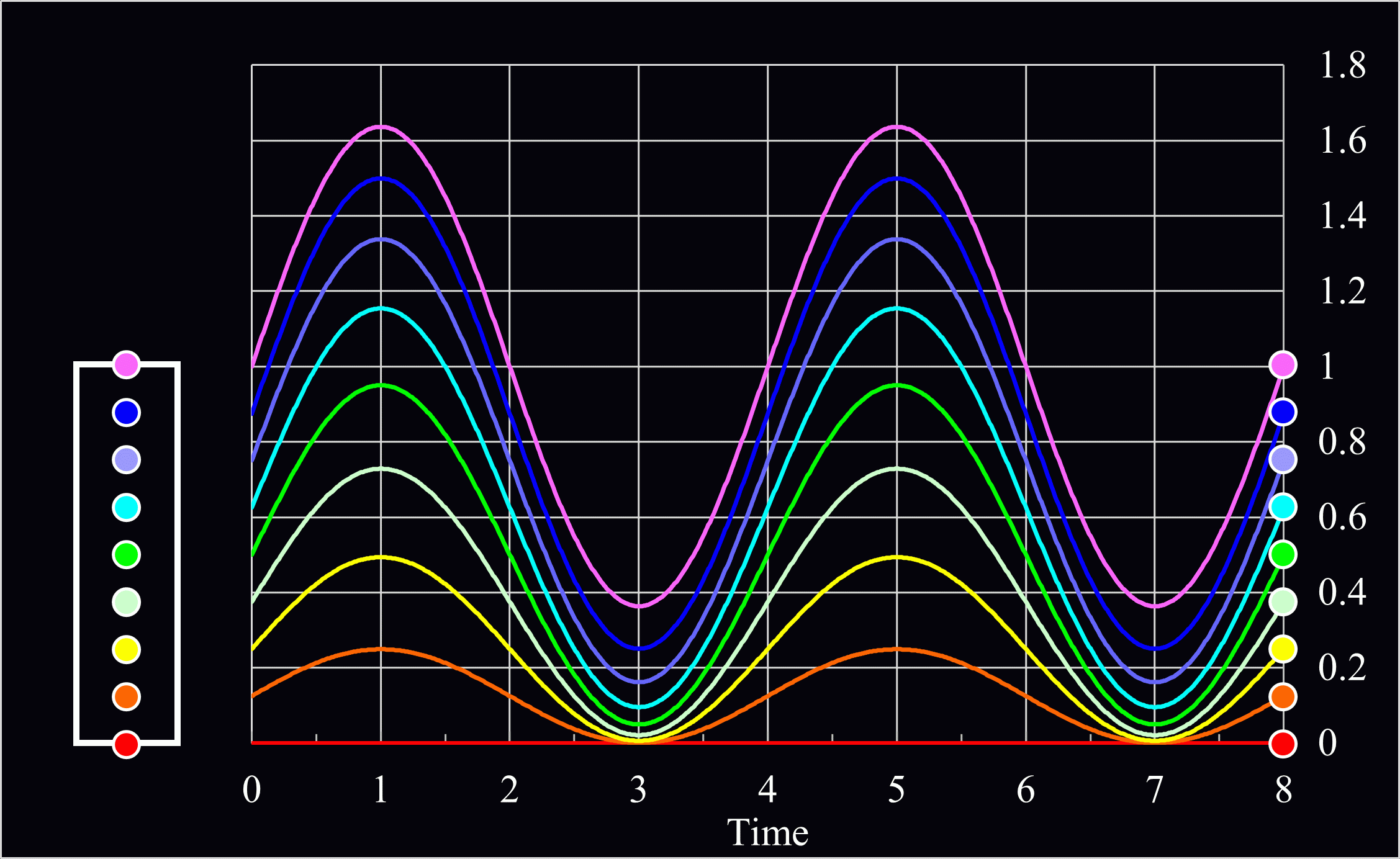
\(l、B、ρ、E、\)初速度は1として計算しています。
このように棒の先端部分に近い紫の点の方が固定部に近いオレンジの点より大きく揺れていることが分かりますね。
まとめ
棒の縦振動の具体例を解説しました。
1次の固有振動モードの形がどのようになるかについてもアニメーションをみることで理解が深まったのではないでしょうか?
波動方程式に具体的に値を入れることで振動の形が決まってきますので、 まずはしっかりと運動方程式を立てる、そして初期条件、境界条件を入れて計算する、という流れを覚えておきましょう。
次回は梁の横振動について解説します。
振動・波動の基礎-㉙連続体の振動 梁の横振動の運動方程式をわかりやすく解説
参考文献
- 振動工学の基礎:岩壺卓三、松久寛、森北出版株式会社
- 機械力学-振動の基礎から制御まで:日高照晃、小田哲、川辺尚志、曽我部雄次、吉田和信、朝倉書店
- 構造と連続体の力学基礎:熊でもわかる変形できる物体の力学:岩熊哲夫、小山茂 web版
初心者向けの振動工学の教科書・参考書をこちらで紹介していますので、参考にしていただければと思います。
初心者向けの教科書・参考書はこちら
振動工学の記事一覧はこちら
次の記事 →振動・波動の基礎-㉙連続体の振動 梁の横振動の運動方程式をわかりやすく解説
