振動・波動の基礎-㉕連続体の振動両端固定の弦の自由振動一般解の具体例をわかりやすく解説 |

連続体の振動の解はわかったんだけど、具体的にどんな形になるのか想像つかないんだけど…

苦手君

デルタ先生

それじゃあ、前回求めた自由振動の一般解に、初期条件を代入して具体的な波形を見てみよう。

今回は両端固定の弦の自由振動をより具体的な形で示します。

前々回の自由振動の運動方程式、前回の自由振動の一般解を用いて解説しますので、そちらをまだ見ていない方は下記のリンクから過去の記事を見てみてください。

過去記事

下記動画でも解説しておりますので、是非参考にしていただければと思います。

モデルと運動方程式

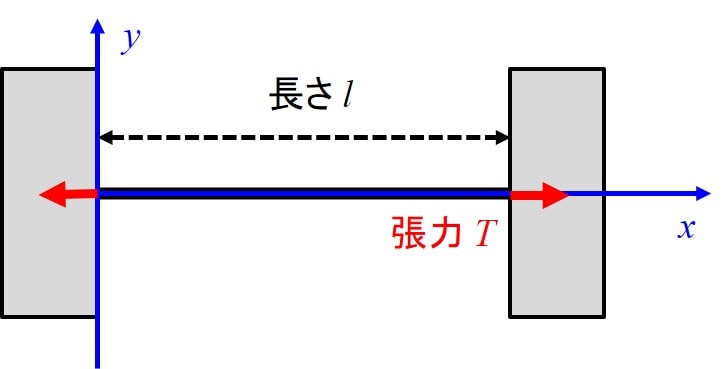
詳細は過去の記事を参考にしてください。

運動方程式は下記のようになります。

$$\frac{\partial^2y}{\partial t^2}=c^2\frac{\partial^2y}{\partial x^2}$$

この$y(x,t)$はたわみ量を示していて、$x$と$t$の関数で表されます。

この$y$を$x$の関数と$t$の関数の積で表せるとして、変数分離法で分離しますと、

$$y(x,t)=Y(x)G(t)$$

という形になります。

一般解と初期条件

一般解を実数化する

$$y(x,t)=Y(x)G(t)$$

これを解いて一般解を求めると、 $$y(x,t)=\sum_{n=1}^{\infty}y_n(x,t)=\sum_{n=1}^{\infty}A_ne^{iω_nt}sin\frac{nπx}{l}$$

複素表示で書くと、上記のような形になりますが、このままだと解の形がイメージしにくいので、実部をとることを考えます。

過去の記事で単振動などを複素数で解いて実数の部分を取り出す、ということを説明していますので、そちらも参考にしていただければと思います。

振幅の$A_n$は複素振幅を示しているので、

$$A_n=a+ib$$

と書くことができ、指数関数の$e^{iω_nt}$の部分はオイラーの公式から

$$e^{iω_nt}=cosω_nt+isinω_nt$$

となりますので、

$$A_ne^{iω_nt}=(a+ib)(cosω_nt+isinω_nt)$$

展開して実部と虚部を分けて書くと、

$$(a+ib)(cosω_nt+isinω_nt)=(acosω_nt-bsinω_nt)+i(asinω_nt+bcosω_nt)$$

と書けます。

ここで実部の部分を一般解として取り出し、cosとsinの係数を次のように書き換えます。

$$a=C_n　、　b=-D_n$$

このように係数を置き換えて実数部分を取り出した一般解は、

$$y(x,t)=\sum_{n=1}^{\infty}sin\frac{nπx}{l}(C_ncosω_nt+D_nsinω_nt)$$

$C_n$と$D_n$は未知数です。

このモデルに対して初期条件として、下記を与え、未知数を決定することを考えます。

$$y(x,0)=y_0(x),\dot{y}(x,0)=v_0(x)$$

初期条件を代入すると

$$y(x,0)=\sum_{n=1}^{\infty}sin\frac{nπx}{l}・C_n=y_0(x)$$

$$\frac{\partial y(x,0)}{\partial t}=\sum_{n=1}^{\infty}sin\frac{nπx}{l}・ω_nD_n=v_0(x)$$

さて、ここまでは代入するだけなので簡単なのですが、未知数を求める際に、ここでフーリエ級数展開の知識を使います。

少しだけフーリエ級数展開の内容を復習しておきましょう。

フーリエ級数展開

とある連続関数f(x)をフーリエ級数展開すると、

$$f(x)=\frac{a_0}{2}+\sum_{n=1}^{\infty}(a_ncosnx+b_nsinnx)$$

と書くことができます。

このフーリエ級数展開の意味するところは、『連続関数f(x)をいろんな周波数の三角関数の重ね合わせで表現していますよ』ということになっています。

ここで、$a_n$と$b_n$はフーリエ係数と呼ばれるもので、下記のように表すことができます。

$$a_m=\frac{1}{π}\int^π_{-π}f(x)cosmxdx$$ $$b_m=\frac{1}{π}\int^π_{-π}f(x)sinmxdx$$

このフーリエ係数は、f(x)を色んな周波数の三角関数の重ね合わせで表した時の、それぞれの三角関数の振幅を意味しています。

どの周波数の三角関数が、どれくらいの割合で入っているかを示している、とも言い換えることができます。フーリエ係数を求めるときは積分を施してもとめます。

この導出については、実際に$f(x)$に$cosmx$や$sinmx$をかけて1周期分積分し、半周期分で割ってあげれば求めることができます。

実際に$cosmx$をかけて積分してあげると、

$$\frac{1}{π}\int^π_{-π}f(x)cosmxdx=\frac{1}{π}\int^π_{-π}(\frac{a_0}{2}+\sum_{n=1}^{\infty}(a_ncosnx+b_nsinnx)cosmxdx$$

第1項について計算すると、

$$\int^π_{-π}\frac{a_0}{2}cosmxdx=\frac{a_0}{2}\frac{1}{m}[sinmx]^π_{-π}=0$$

このようにゼロになります。

次に$\sum$の中の$a_ncosnx$の項について計算してみましょう。

$$\int^π_{-π}a_ncosnx・cosmxdx=\frac{a_n}{2}\int^π_{-π}\{cos(n+m)x+cos(n-m)x\}dx$$

これを積分すると、$n=m$のとき、分母がゼロとなる項が出てきてしまうので、場合分けをします。

$n=m$のとき

$$\begin{eqnarray}&&\frac{a_m}{2}\int^π_{-π}\{cos(n+m)x+cos(n-m)x\}dx\\&=&\frac{a_m}{2}\int^π_{-π}(cos2mx+1)dx=\frac{a_m}{2}\left[\frac{1}{2m}sin2mx+x\right]^π_{-π}\\&=&a_m\end{eqnarray}$$

$n≠m$のとき

$$\begin{eqnarray}&&\frac{a_n}{2}\int^π_{-π}\{cos(n+m)x+cos(n-m)x\}dx\\&=&\frac{a_n}{2}\left[\frac{sin(n+m)x}{n+m}+\frac{sin(n-m)x}{n-m}\right]^π_{-π}\end{eqnarray}$$

ここで、$n,m$は自然数なので、積分の値はゼロとなります。

よって、

$$\int^π_{-π}\sum_{n=1}^{\infty}a_ncosnx・cosmxdx=a_m$$

となります。

それでは次に$\sum$の中の$b_nsinnx$の項について計算してみましょう。

$$\begin{eqnarray}&&\int^π_{-π}b_nsinnx・cosmxdx\\&=&\frac{b_n}{2}\int^π_{-π}\{sin(n+m)x+sin(n-m)x\}dx\end{eqnarray}$$

これも積分すると、$n=m$のとき、分母がゼロとなる項が出てきてしまうので、場合分けをします。

$n=m$のとき

$$\begin{eqnarray}&&\frac{b_m}{2}\int^π_{-π}\{sin(n+m)x+sin(n-m)x\}dx\\&=&\frac{b_m}{2}\int^π_{-π}sin2mxdx=\frac{b_m}{2}\left[\frac{-1}{2m}cos2mx\right]^π_{-π}\\&=&0\end{eqnarray}$$

$n≠m$のとき

$$\begin{eqnarray}&&\frac{b_m}{2}\int^π_{-π}\{sin(n+m)x+sin(n-m)x\}dx\\&=&\frac{b_m}{2}\left[\frac{-cos(n+m)x}{n+m}+\frac{-cos(n-m}x{n-m}\right]^π_{-π}\\&=&0\end{eqnarray}$$

よって、

$$\int^π_{-π}\sum_{n=1}^{\infty}b_nsinnx・cosmxdx=0$$

となり、以上、まとめると、

$$\frac{1}{π}\int^π_{-π}f(x)cosmxdx=a_m$$

となって、$cos$側のフーリエ係数が求まるわけです。

$sin側$のフーリエ係数$b_m$を求めるには、$cosmx$ではなく、$sinmx$をかけて積分すれば求めることができます。

今回は$sin$側のフーリエ係数をもとめるので、こちらは今回の問題に沿って計算してみましょう。

フーリエ級数展開を使って計算

今回は$y_0(x)、v_0(x)$についてフーリエ級数展開とフーリエ係数の関係を利用して未知数$C_n,D_n$を求めます。

まず、$y_0$についてです。

$$y_0(x)=\sum_{n=1}^{\infty}sin\frac{nπx}{l}・C_n$$

この式には$cos$の項がありませんが、$cos$の項のフーリエ係数をゼロとして、$y_0(x)$をフーリエ級数展開したという風に読み替えることができます。

ということで、$sin$の項のフーリエ係数を求めましょう。

フーリエ係数の公式は下記でしたね。

$$b_m=\frac{1}{π}\int^π_{-π}f(x)sinmxdx$$

$m→\frac{mπ}{l}$として$y_0(x)$に$sin\frac{mπx}{l}$をかけて、1周期分の積分をします。

$π～-π$までの積分は、$l～-l$までの積分となるので、

$$C_n=\frac{1}{l}\int^l_{-l}\sum_{n=1}^{\infty}y_0(x)sin\frac{mπx}{l}dx$$

このように書けます。

あとは初期条件の$y_0(x)$に与えられた関数を代入すればOKです。

$D_n$も同様に求めることができて、

$$v_0(x)=\sum_{n=1}^{\infty}sin\frac{nπx}{l}・ω_nD_n$$

であったので、両辺を$ω_n$で割って

$$\frac{v_0(x)}{ω_n}=\sum_{n=1}^{\infty}sin\frac{nπx}{l}D_n$$

として、左辺がフーリエ級数展開されたとして見て、フーリエ係数を求めます。

$$D_n=\frac{1}{lω_n}\int^l_{-l}\sum_{n=1}^{\infty}v_0(x)sin\frac{mπx}{l}dx$$

こちらも初期速度が初期条件で与えられたとき、$v_0$に代入すればOKです。

具体例を計算してみる

それでは下記のような初期条件を入れて、実際に計算してみましょう。

$$0≦x≦\frac{l}{2}のとき、y_0(x)=\frac{2y_0}{l}x$$

$$\frac{l}{2}≦x≦lのとき、y_0(x)=2y_0(1-\frac{x}{l})$$

具体的に図で書くと下記のような初期状態ですね。

それではフーリエ係数を求めて、一般解の形に入れて、振動の形を求めましょう。

まずは$C_n$です。

$$C_n=\frac{1}{l}\int^l_{-l}\sum_{n=1}^{\infty}y_0(x)sin\frac{mπx}{l}dx$$

さきほど、このような形で求まっていたので、初期変位の関数を入れて計算します。

また、計算を簡単にするためにsin関数の積分なので積分区間を$l～0$にして2倍して計算します。

$$C_n=\frac{2}{l}\int^{\frac{l}{2}}_0\frac{2y_0}{l}xsin\frac{nπ}{l}xdx+\frac{2}{l}\int^{\frac{l}{2}}_02y_0(1-\frac{x}{l})sin\frac{nπ}{l}xdx$$

このように積分が二つ出てくるので、下記のように第1項と第2項の積分を$C_{n1}$、$C_{n2}$と置きます。

$$C_{n1}=\frac{2}{l}\int^{\frac{l}{2}}_0\frac{2y_0}{l}xsin\frac{nπ}{l}xdx$$

$$C_{n2}=\frac{2}{l}\int^l_{\frac{l}{2}}2y_0(1-\frac{x}{l})sin\frac{nπ}{l}xdx$$

これらを具体的に計算していきます。

$$C_{n1}=\frac{4y_0}{l^2}\int^{\frac{l}{2}}_0xsin\frac{nπ}{l}xdx$$

部分積分を行って、

$$C_{n1}=\frac{4y_0}{l^2}\left(\left[-x\frac{l}{nπ}cos\frac{nπ}{l}x\right]^{\frac{l}{2}}_0+\frac{l}{nπ}\int^{\frac{l}{2}}_0cos\frac{nπ}{l}xdx\right)$$

これらを計算すると

$$\begin{eqnarray}C_{n1}&=&\frac{4y_0}{l^2}\left(\left(-\frac{l^2}{2nπ}cos\frac{nπ}{2}\right)+(\frac{l}{nπ})^2\left[sin\frac{nπ}{l}x\right]^{\frac{l}{2}}_0\right)\\ &=&-\frac{4y_0}{nπ}\left(\frac{1}{2}cos\frac{nπ}{2}-\frac{1}{nπ}sin\frac{nπ}{2}\right)\end{eqnarray}$$

次に$C_{n2}$を計算すると、

$$\begin{eqnarray}C_{n2}&=&\frac{2}{l}\int^l_{\frac{l}{2}}2y_0(1-\frac{x}{l})sin\frac{nπ}{l}xdx\\&=&\frac{4y_0}{l}\left(\int^l_{\frac{l}{2}}sin\frac{nπ}{l}xdx-\frac{1}{l}\int^l_{\frac{l}{2}}xsin\frac{nπ}{l}xdx\right)\\&=&\frac{4y_0}{l}\left(\left[\frac{-l}{nπ}cos\frac{nπ}{l}x\right]^l_{\frac{l}{2}}-\frac{1}{l}\left(\left[\frac{-l}{nπ}xcos\frac{nπ}{l}x\right]^l_{\frac{l}{2}}-\int^l_{\frac{l}{2}}\frac{-l}{nπ}cos\frac{nπ}{l}xdx\right)\right) \\&=&\frac{4y_0}{l}\left(\frac{-l}{nπ}cosnπ+\frac{l}{nπ}cos\frac{nπ}{2}-\frac{1}{l}\left(-\frac{l^2}{nπ}cosnπ+\frac{l^2}{2nπ}cos\frac{nπ}{2}+\frac{l}{nπ}\left[\frac{l}{nπ}sin\frac{nπ}{l}x\right]^l_{\frac{l}{2}}\right)\right) \\&=&\frac{4y_0}{nπ}\left(-cosnπ+cos\frac{nπ}{2}\right)-\frac{4y_0}{l^2}\left(-\frac{l^2}{nπ}cosnπ+\frac{l^2}{2nπ}cos\frac{nπ}{2}+\left(\frac{l}{nπ}\right)^2\left(sinnπ-sin\frac{nπ}{2}\right)\right) \\&=&\frac{4y_0}{nπ}\left(-cosnπ+cos\frac{nπ}{2}\right)+\frac{4y_0}{nπ}\left(cosnπ-\frac{1}{2}cos\frac{nπ}{2}+\frac{1}{nπ}sin\frac{nπ}{2}\right) \\&=&-\frac{4y_0}{nπ}\left(cosnπ-cos\frac{nπ}{2}\right)+\frac{4y_0}{nπ}\left(cosnπ-\frac{1}{2}cos\frac{nπ}{2}+\frac{1}{nπ}sin\frac{nπ}{2}\right)\end{eqnarray}$$

よって$C_n$は$C_{n1}$と$C_{n2}$の和なので、下記のように求まります。

$$C_n=\frac{8y_0}{(nπ)^2}sin\frac{nπ}{2}$$

また、$D_n$については、初期速度$v_0=0$なので、$D_n=0$となります。

自由振動の一般解は、

$$y(x,t)=\sum_{n=1}^{\infty}sin\frac{nπx}{l}(C_ncosω_nt+D_nsinω_nt)$$

なので、求めた$C_n$と$D_n$を代入すると

$$y(x,t)=\sum_{n=1}^{\infty}sin\frac{nπx}{l}C_ncosω_nt$$ $$=\sum_{n=1,3,…}^{\infty}sin\frac{nπx}{l}\frac{8y_0}{(nπ)^2}sin\frac{nπ}{2}cosω_nt$$

このように、今回与えた初期条件では、1次、3次…と奇数次のモードの重ね合わせになっていることが分かります。

式だけ見てもイメージがつかない方のためにアニメーションで確認してみましょう。

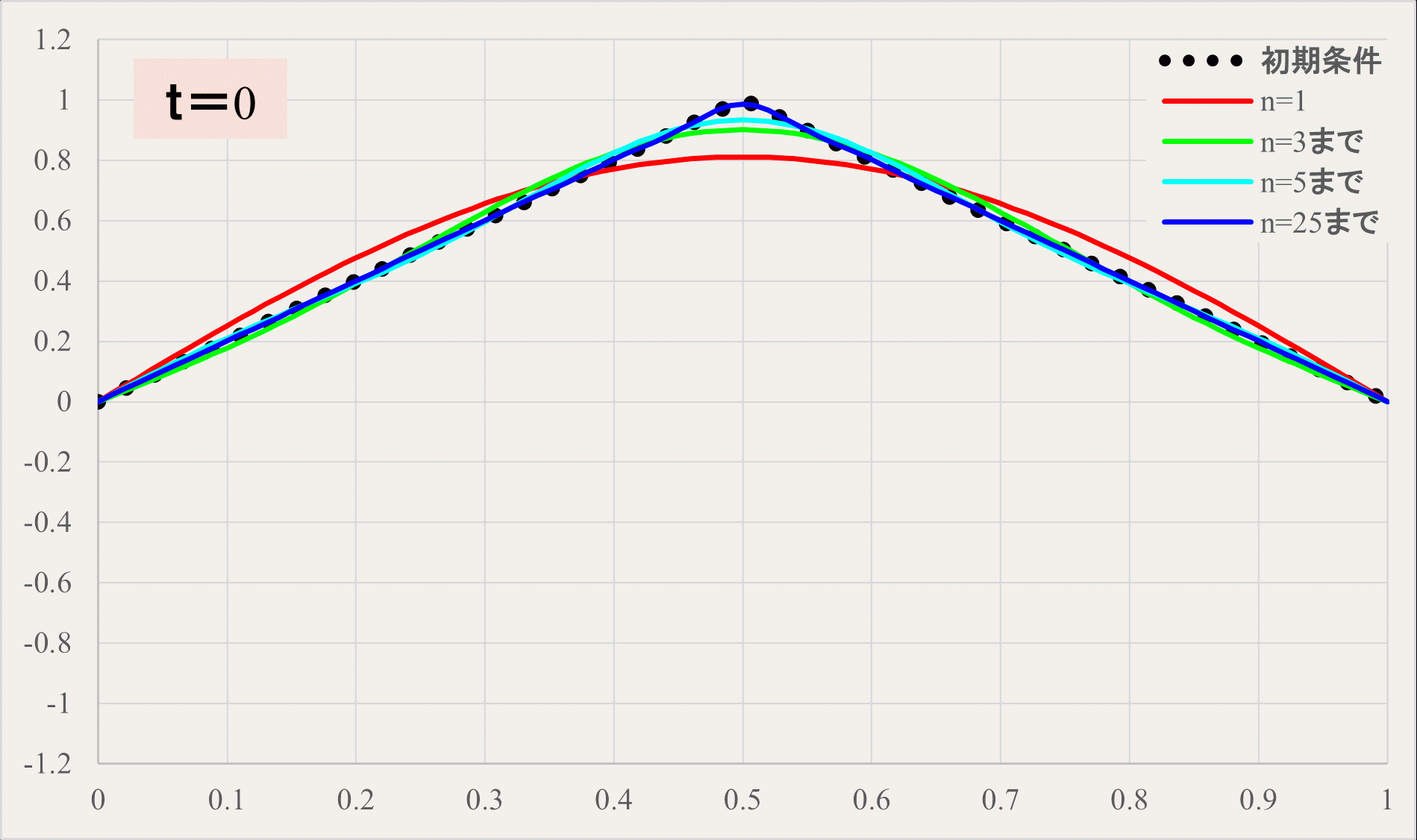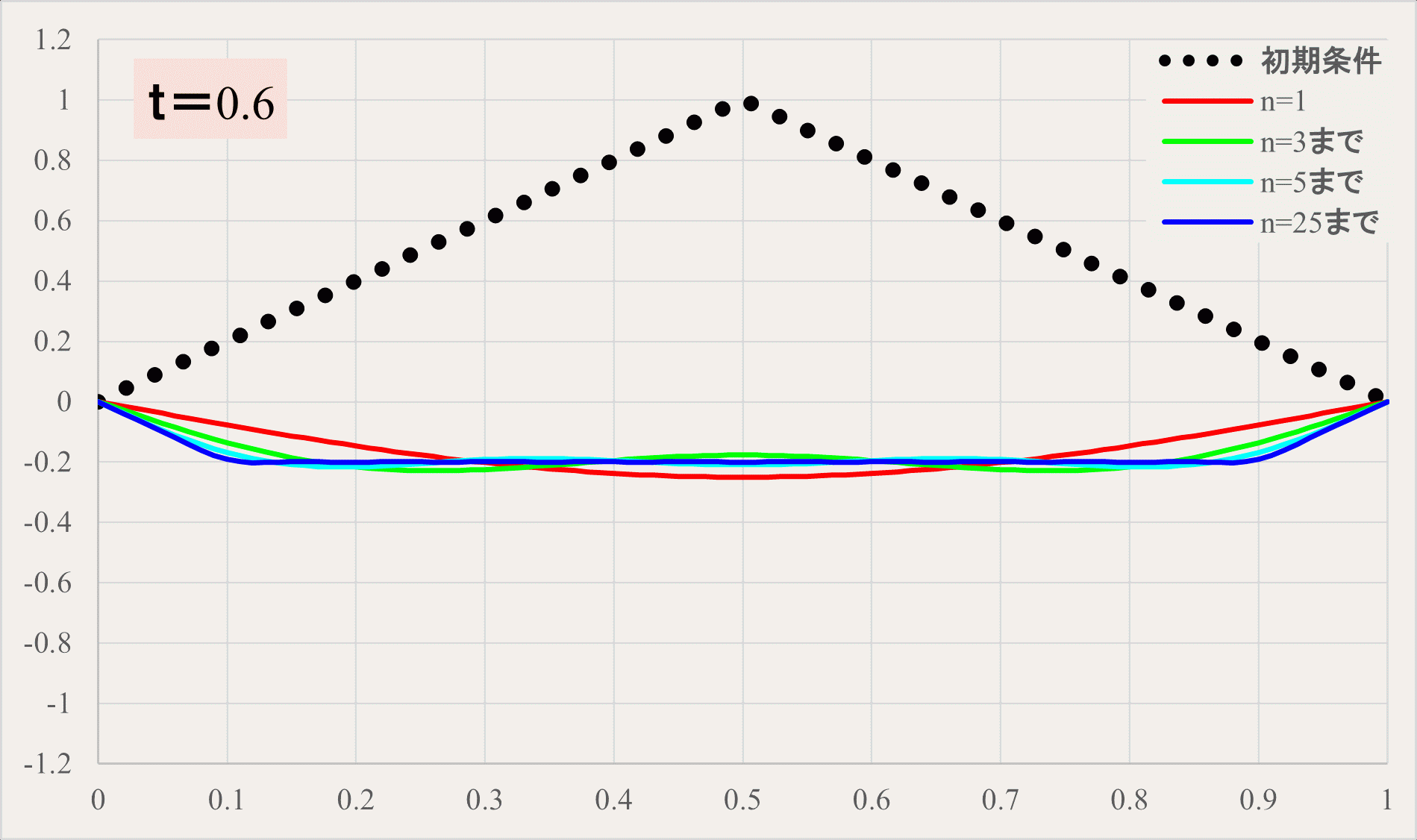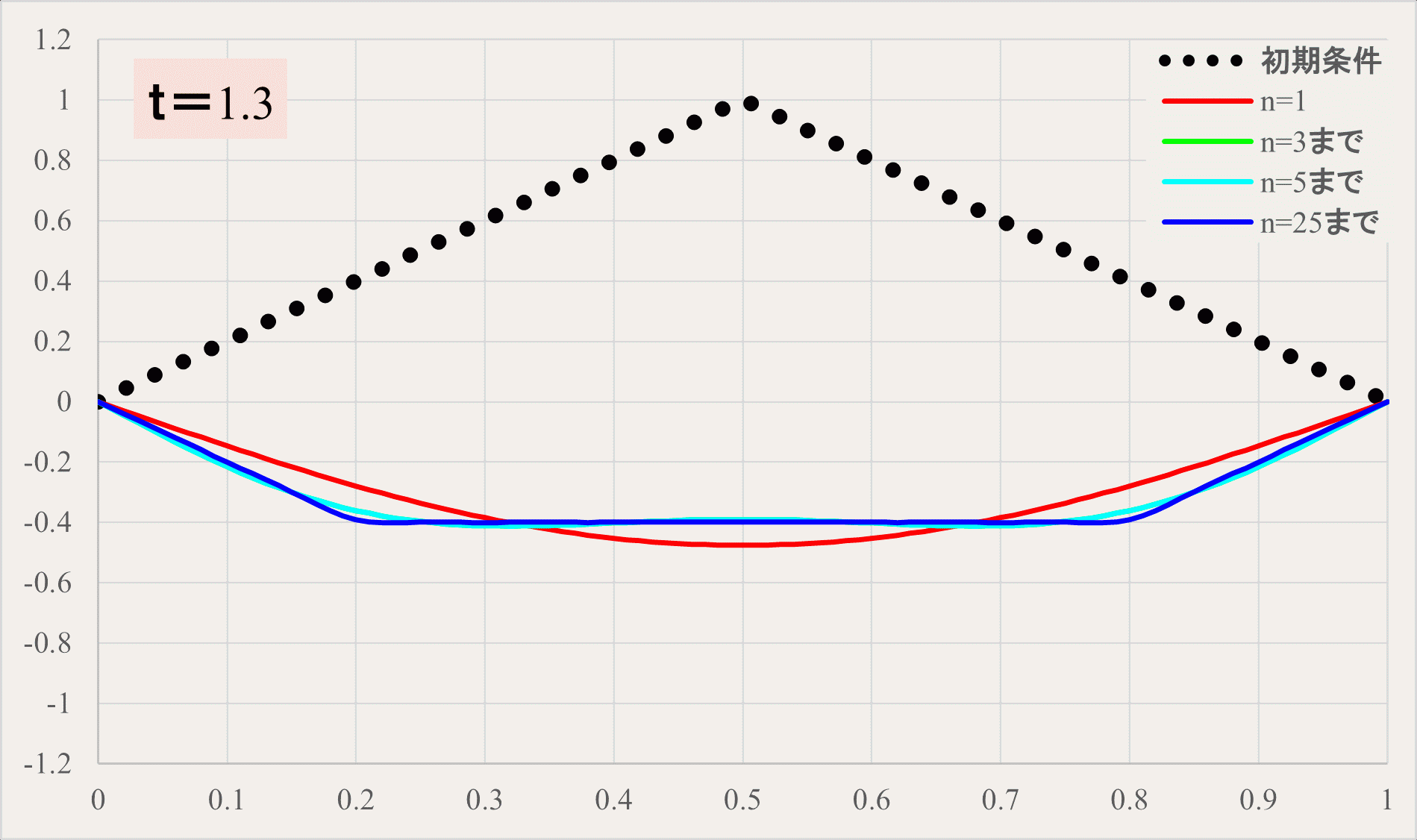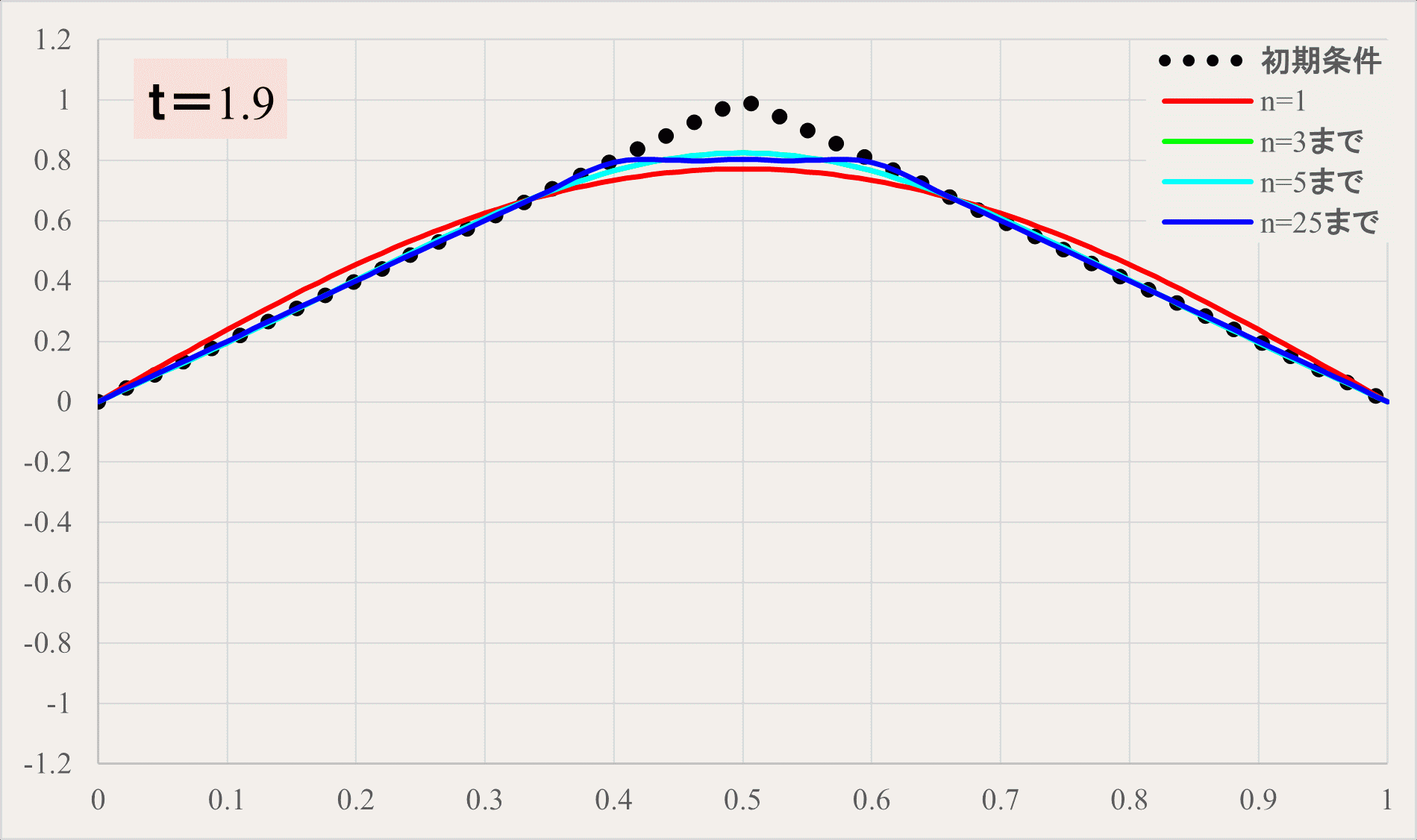
黒の点線が初期状態、赤の線が$n=1$までの三角関数の和、緑の線が$n=3$まで、水色が$n=5$まで、青が$n=25$までの三角関数の和のラインを示しています。

青の$n=25$くらいまで和をとると、ほとんど$n=∞$の結果と変わらなくなります。

実際には減衰の効果があるので、初期条件の部分まで戻ってくることはありませんが、理想的な弦の場合、このような形で振動します。

下記に各成分の三角関数の波形の時間変化を示します。

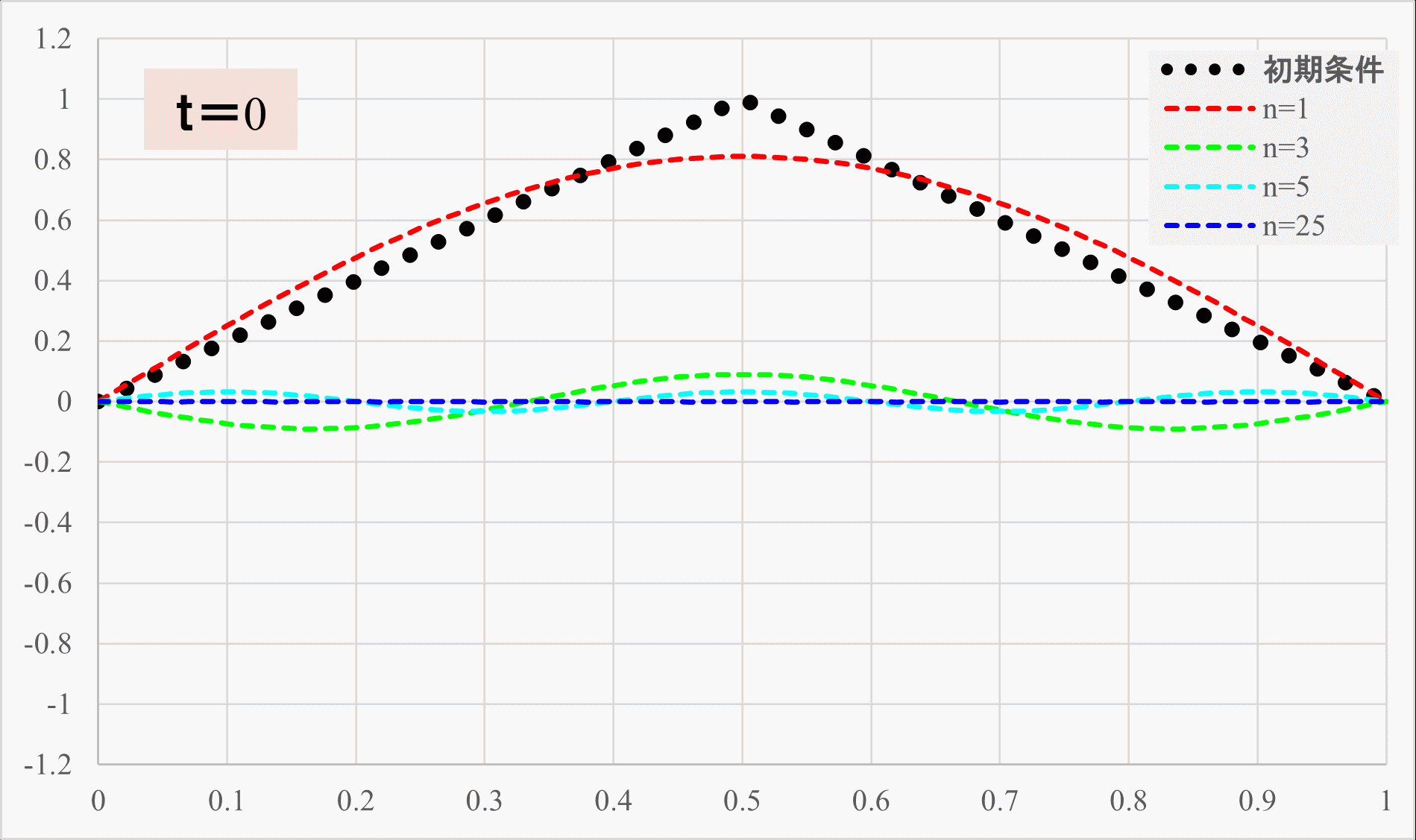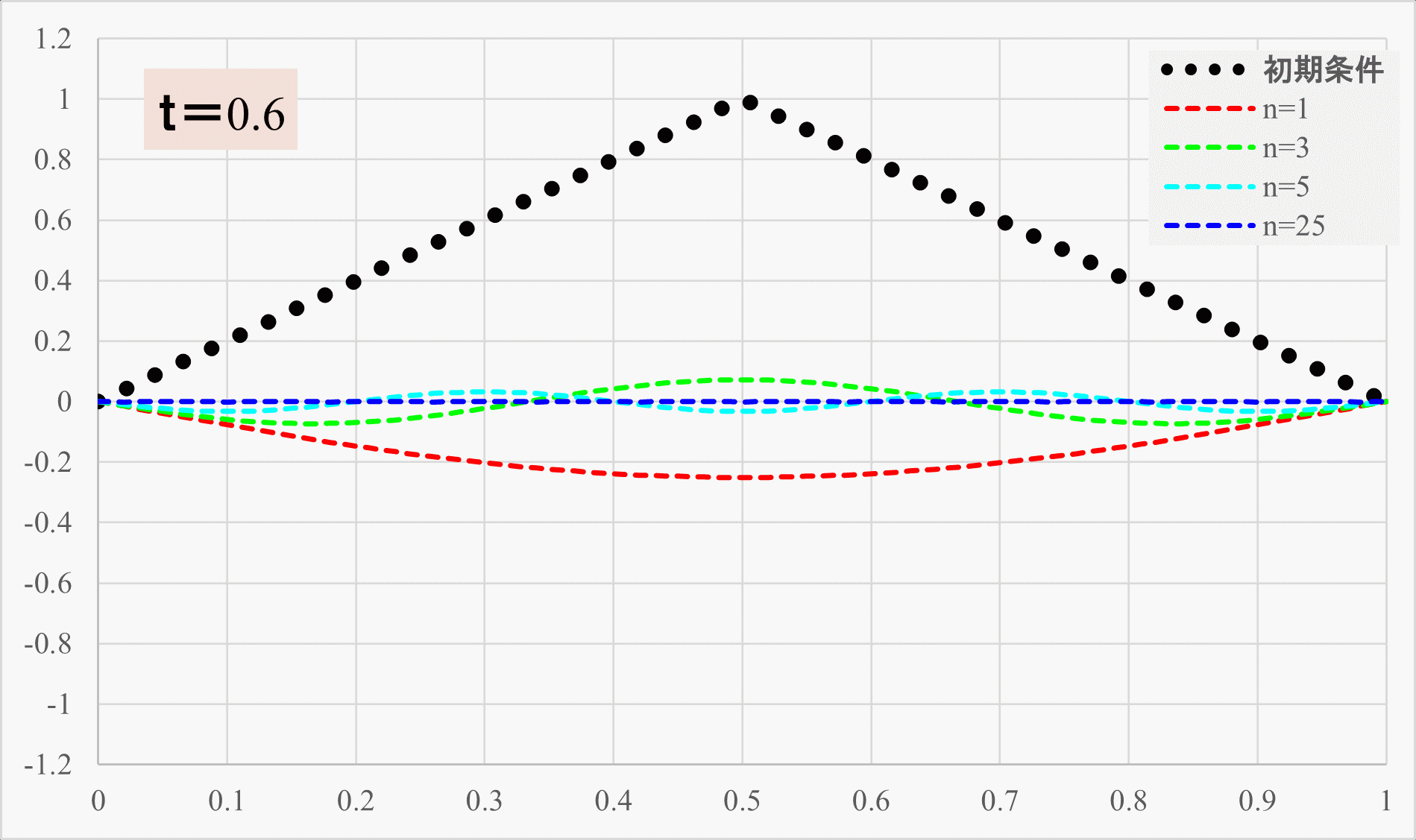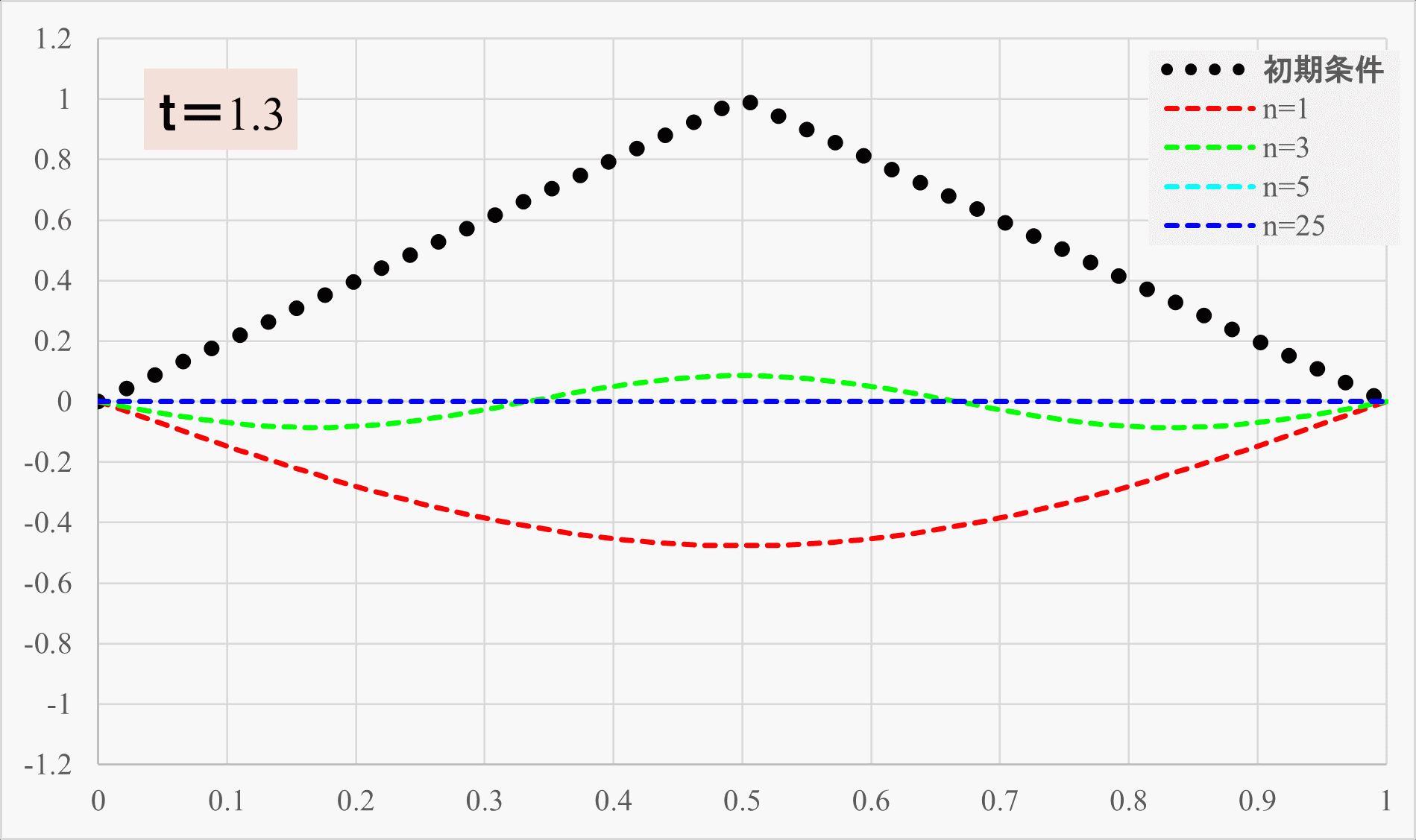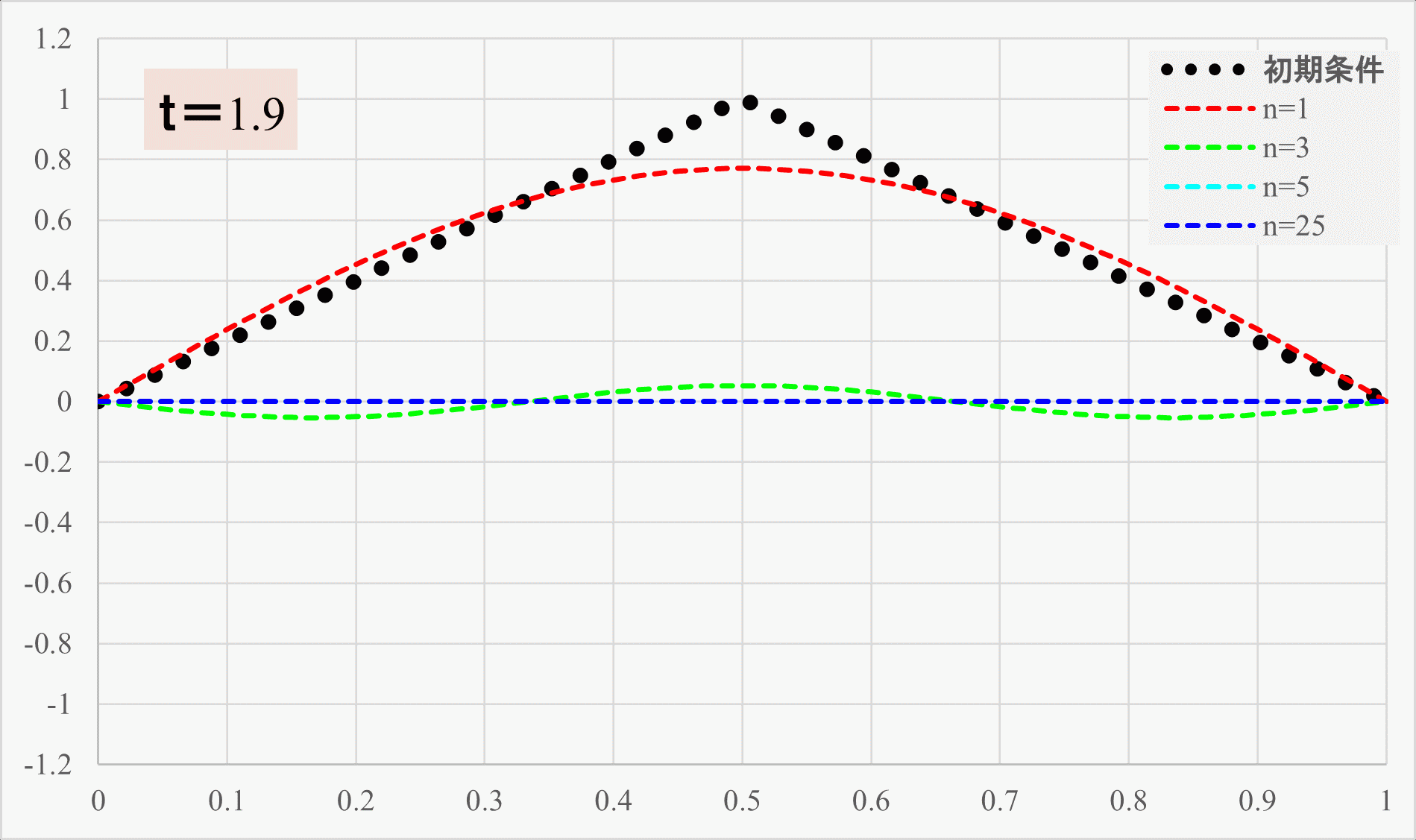
メインは赤のラインの$n=1$の三角関数で構成されているものの、緑や水色の成分が足されることで、先ほどの$n=25$までの和のような弦の振動が実現されているわけですね。

まとめ

今回は連続体の自由振動の一般解と具体例について解説しました。

具体例を考えるにあたって、フーリエ級数展開の知識が重要となってきますので、フーリエ級数展開の数学的知識も解説しました。

フーリエ級数展開やフーリエ変換は振動・波動の分野では頻出の数学知識ですので、しっかりと理解しておくようにしましょう。

参考文献

振動工学の基礎：岩壺卓三、松久寛、森北出版株式会社
機械力学-振動の基礎から制御まで：日高照晃、小田哲、川辺尚志、曽我部雄次、吉田和信、朝倉書店
構造と連続体の力学基礎：熊でもわかる変形できる物体の力学：岩熊哲夫、小山茂 web版

初心者向けの振動工学の教科書・参考書をこちらで紹介していますので、参考にしていただければと思います。

初心者向けの教科書・参考書はこちら

振動工学の記事一覧はこちら

次の記事 → 振動・波動の基礎-㉕連続体の振動両端固定の弦の自由振動一般解の具体例をわかりやすく解説

振動・波動の基礎-㉕連続体の振動 両端固定の弦の自由振動一般解の具体例をわかりやすく解説