物理苦手君
デルタ先生今回は両端固定の弦の強制振動を解説します。
自由振動については、過去の記事で解説していますので、そちらを参考にしてくださいね。
モデルと運動方程式
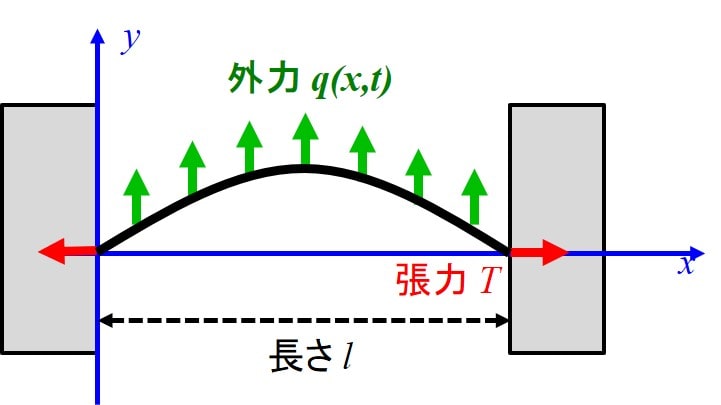
モデルの詳細は過去の記事を参考にしてください。
弦の運動方程式は
$$\frac{\partial^2y}{\partial t^2}=c^2\frac{\partial^2y}{\partial x^2}+\frac{1}{μ}q(x,t)$$
このように２階の偏微分方程式で表すことができます。
強制振動の解
運動方程式から非同次の微分方程式になっており、この解は多自由度系などと同じく、自由振動の一般解と強制振動の特殊解で表されます。
自由振動の一般解については、前回までの過去記事で紹介していますので、そちらを参考にしてください。
ということで、今回は強制振動の特殊解について取り扱います。
強制振動の特殊解を下記のように固有振動モードの重ね合わせで表現できるとして進めます。
$$y(x,t)=\sum^{\infty}_{n=1}sin\left(\frac{nπ}{l}x\right)H_n(t)$$
$H_n(t)$は未知の時間の関数で、これを具体的な強制力等から定めることで、具体的に特殊解が求まることになります。
しかし、このままだと強制力を定めても求めることができないので、$H_n(t)$を求めるために、$H_n$の微分方程式になるように、運動方程式を変形していきます。
まず、仮定した特殊解を運動方程式に代入します。
$$\frac{\partial^2}{\partial t^2}\left(\sum^{\infty}_{n=1}sin\left(\frac{nπ}{l}x\right)H_n(t)\right)=c^2\frac{\partial^2}{\partial x^2}\left(\sum^{\infty}_{n=1}sin\left(\frac{nπ}{l}x\right)H_n(t)\right)+\frac{q}{μ}$$
$\sum$があったりで、このままだと計算の見通しが非常に悪いので、ここで数学的なテクニックを使います。
$sin$関数の$\sum$がありますので、ここを整理するために、両辺に$sin\frac{mπ}{l}x$をかけて0からlまで積分します。
左辺の計算
それではまず左辺について計算していきます。
左辺に$sin\frac{mπ}{l}$をかけると、
$$\frac{\partial^2}{\partial t^2}\left(\sum^{\infty}_{n=1}sin\left(\frac{nπ}{l}x\right)H_n(t)\right)sin\frac{mπ}{l}x=\frac{\partial^2}{\partial t^2}\left(\sum^{\infty}_{n=1}\frac{1}{2}\left(cos\frac{m-n}{l}πx-cos\frac{m+n}{l}πx\right)H_n(t)\right)$$
これを0からlまで積分すると
$$\int^l_0\frac{\partial^2}{\partial t^2}\left(\sum^{\infty}_{n=1}\frac{1}{2}\left(cos\frac{m-n}{l}πx-cos\frac{m+n}{l}πx\right)H_n(t)\right)dx$$
上式の偏微分の中の積分はm=nのとき、分母がゼロとなってしまう項がでてきてしまうので、場合分けを行います。
$m≠n$のとき、第1項の積分は
$$\int^l_0cos\frac{m-n}{l}πxdx=\frac{l}{(m-n)π}\left[sin\frac{m-n}{l}πx\right]^l_0=0$$
第2項の積分は
$$\int^l_0cos\frac{m+n}{l}πxdx=\frac{l}{(m+n)π}\left[sin\frac{m+n}{l}πx\right]^l_0=0$$
$m=n$のとき、
$$\int^l_0\frac{1}{2}\left(1-cos\frac{2mπ}{l}x\right)dx=\frac{1}{2}\left[x-\frac{l}{2mπ}sin\frac{2mπ}{l}x\right]^l_0=\frac{1}{2}l$$
以上より、偏微分の中の積分の値が求まったので、左辺の値は
$$左辺=\frac{l}{2}\frac{\partial^2H_n(t)}{\partial t^2}$$
右辺の計算
次に右辺について計算します。右辺第1項は$sin\frac{mπ}{l}x$をかけると下記のようになります。
$$c^2\frac{\partial^2}{\partial x^2}\left(\sum^{\infty}_{n=1}sin\frac{nπ}{l}x・sin\frac{mπ}{l}x\right)H_n(t)$$
これも0からlまで積分をすると、
$$\begin{eqnarray}&&c^2H_n(t)\int^l_0\frac{\partial^2}{\partial x^2}\sum^{\infty}_{n=1}sin\frac{nπ}{l}x・sin\frac{mπ}{l}xdx\\&=&c^2H_n(t)\int^l_0\frac{\partial^2}{\partial x^2}\sum^{\infty}_{n=1}\frac{1}{2}\left(cos\frac{m-n}{l}πx-cos\frac{m+n}{l}πx\right)dx\\&=&c^2H_n(t)\int^l_0\sum^{\infty}_{n=1}\frac{1}{2}\left(-\frac{(m-n)^2π^2}{l^2}cos\frac{m-n}{l}πx+\frac{(m+n)^2π^2}{l^2}cos\frac{m+n}{l}πx\right)dx\end{eqnarray}$$
このように積分の計算は、左辺を計算したときと同じように計算できて、m=nとm≠nの場合分けが必要となります。
積分の計算自体は、左辺の積分と同じですのでm≠nのときはゼロであり、m=nの時を計算すると、
$$右辺第1項=-c^2H_m(t)\left(\frac{2mπ}{l}\right)^2\frac{l}{2}$$
最後に右辺の第2項は$sin\frac{mπ}{l}$をかけて0からlまで積分すると
$$\frac{1}{μ}\int^l_0q(x,t)sin\frac{mπ}{l}xdx$$
以上より、運動方程式に仮定した特殊解を代入し、$sin\frac{mπ}{l}$をかけて0からlまで積分した結果は、
$$\frac{l}{2}\frac{\partial^2H_m(t)}{\partial t^2}=-c^2H_m(t)\left(\frac{2mπ}{l}\right)^2\frac{l}{2}+\frac{1}{μ}\int^l_0q(x,t)sin\frac{mπ}{l}xdx$$
さらに式を整理する
両辺を$\frac{l}{2}$で割って、右辺の第1項を左辺に移項すると、
$$\frac{\partial^2H_m(t)}{\partial t^2}+c^2H_m(t)\left(\frac{2mπ}{l}\right)^2=\frac{2}{μl}\int^l_0q(x,t)sin\frac{mπ}{l}xdx$$
ここで、左辺第2項の係数について、両端固定弦のm次の固有振動数が下記のように表されるので、係数を置き換えてすっきりさせましょう。（過去記事参考）
$$ω_m=\frac{2πmc}{l}$$
左辺第2項の係数を置き換えると、
$$\frac{\partial^2H_m(t)}{\partial t^2}+ω^2_mH_m(t)=\frac{2}{μl}\int^l_0q(x,t)sin\frac{mπ}{l}xdx$$
このように2階の非同次微分方程式の形に式変形できました。
具体的に強制外力を与えてみる
それでは強制外力を与えて、特殊解がどのようになるかを見てみましょう。
強制外力$q(x,t)=q_0sinωt$とすると、右辺の強制外力の項は、
$$\begin{eqnarray}\frac{2}{μl}\int^l_0q_0sinωtsin\frac{mπ}{l}xdx&=&\frac{2q_0}{μl}sinωt\int^l_0sin\frac{mπ}{l}xdx\\&=&-\frac{2q_0}{mπμ}sinωt(cosmπ-1)\end{eqnarray}$$
ここで$cosmπ=(-1)^m$なので、
$$mが奇数のとき 右辺=\frac{4q_0}{mπμ}sinωt$$
$$mが偶数のとき 右辺=0$$
となります。 右辺に上記mが奇数の場合を代入すると、微分方程式は、
$$\frac{\partial^2H_m(t)}{\partial t^2}+ω^2_mH_m(t)=\frac{4q_0}{mπμ}sinωt$$
ここまでくれば、右辺の$sinωt$の係数を周期的外力の振幅$f$とすることで、1自由度の減衰無し強制振動の運動方程式と同じ解き方ができますね。
過去の記事で解説していますので、参考にしてください。
ちなみに1自由度の質点のときの周期的外力の振幅は$F$であり、$f=\frac{F}{m}$であることに注意してください。
$H_m(t)$の特殊解の形は1自由度の強制振動の結果を流用して下記のようになります。
$$H_m(t)=\frac{4q_0}{mπμ}\frac{sinωt}{ω^2_m-ω^2}$$
$H_m(t)$が求まったので、最初に仮定した$y(x,t)$の特殊解に代入すると、
$$y(x,t)=\sum^{\infty}_{n=1}sin\left(\frac{nπ}{l}x\right)H_n(t)=\sum^{\infty}_{m=1,3,…}sin\left(\frac{mπ}{l}x\right)\frac{4q_0}{mπμ}\frac{sinωt}{ω^2_m-ω^2}$$
この特殊解の形を見てみると、分母に$ω^2_m-ω^2$が存在しているので、弦の固有振動数$ω_m$と周期的外力の振動数$ω$が等しいとき、共振が起こり、振幅が無限大になってしまうことがわかりますね。
ちなみに、今回のケースでは、$m$は奇数しか許されていないので、共振が起こるのは1次、3次、…と奇数次の固有振動数と周期的外力が一致するときだけとなります。
まとめ
今回は連続体の強制振動について解説しました。
連続体でも固有振動数と周期的外力の振動数が一致すると共振することが理解できたと思います。
また、今回紹介したような、周期的外力が弦全体に均一にかかっている場合、奇数次の固有振動数で共振が起こります。
このあたりは周期的外力がどのように仮定されるかで変わってきますので、しっかり計算できるようにしておきましょう。
参考文献
- 振動工学の基礎：岩壺卓三、松久寛、森北出版株式会社
- 機械力学-振動の基礎から制御まで：日高照晃、小田哲、川辺尚志、曽我部雄次、吉田和信、朝倉書店
- 構造と連続体の力学基礎：熊でもわかる変形できる物体の力学：岩熊哲夫、小山茂 web版
初心者向けの振動工学の教科書・参考書をこちらで紹介していますので、参考にしていただければと思います。
本サイトの振動工学のページはこちら。
