自由振動のエネルギーはわかったんだけど、強制振動の場合エネルギーってどうなるの?

苦手君

デルタ先生
じゃあ今回は強制振動のエネルギーについて勉強しよう。
本日は強制振動のエネルギーについて学習します。
これまで下記の記事で単振動、減衰振動のエネルギーについて学習しました。
振動・波動の基礎 振動をエネルギーの観点から理解する-減衰振動、散逸関数
強制振動のポイントとして周期的外力によるエネルギーについてしっかりと理解し、散逸関数との関係性を覚えておきましょう。
動画でも解説していますので参考にしてください。
強制振動の復習
詳細は下記の過去記事、動画で解説していますので参考にしてください。
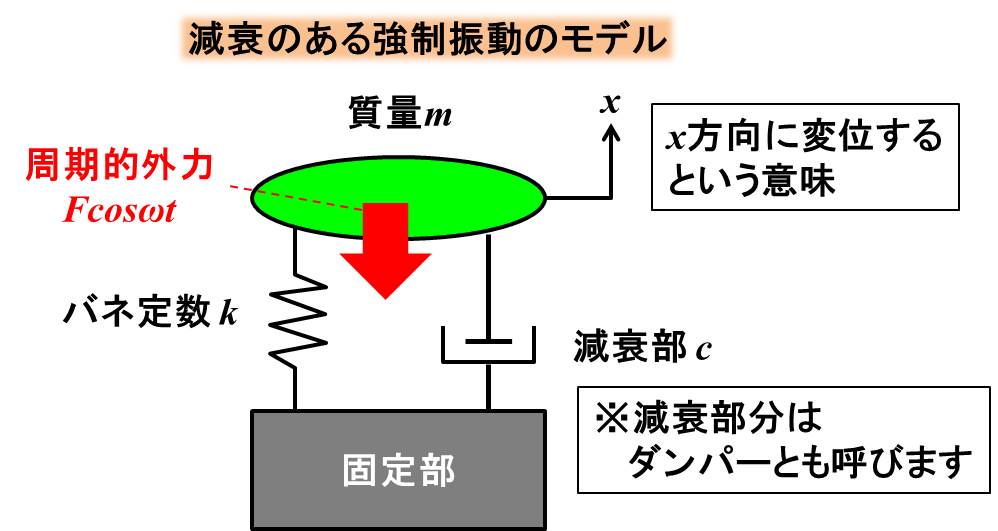
モデルと運動方程式
モデルは上記のようになっています。
質量がm、減衰係数c、バネ定数k、周期的外力を\(Fcosωt\)とします。
この場合の運動方程式は下記のようになります。
$$m\ddot{x}+c\dot{x}+kx=Fcosωt$$
この運動方程式を解いて、変位の式を求めると、
$$tanδ = \frac{2ζω_0ω}{ω_0^2-ω^2}$$
$$ζ = \frac{c}{2\sqrt{mk}}$$
$$ω_0 = \sqrt{\frac{k}{m}}$$
$$f =\frac{F}{m}$$
変位の式は三角関数の合成で\(sin\)の式だけで書き表されていますが、今回の計算では、\(sin\)と\(cos\)の2つで表した方が楽になりますので、分割します。
振動のエネルギー
運動エネルギーを\(V\)、バネの弾性エネルギーを\(U\)、散逸関数を\(D\)とすると、それぞれ下記のように表すことができます。
$$V=\frac{1}{2}mv^2$$
$$U=\frac{1}{2}kx^2$$
$$D=\frac{1}{2}cv^2$$
力学的エネルギー\(E\)は\(V\)と\(U\)の和で表されるので、
$$E=V+U$$
この力学的エネルギーが時間的にどのように変化するかを見てみましょう。
力学的エネルギー\(E\)を時間微分すると、
$$\begin{eqnarray}\frac{dE}{dt}&=&\frac{d}{dt}(\frac{1}{2}mv^2+\frac{1}{2}kx^2)\\\\&=&mv\frac{dv}{dt}+kx\frac{dx}{dt}\\\\&=&mv\frac{d^2x}{dt^2}+kxv \\\\&=&v(m\ddot{x}+kx)\end{eqnarray}$$
運動方程式から、
$$m\ddot{x}+kx=-c\dot{x}+Fcosωt$$
なので、これを代入すると、
$$\begin{eqnarray}v(m\ddot{x}+kx)&=&v(-c\dot{x}+Fcosωt)\\\\ &=&-cv^2+vFcosωt\\\\&=&-2D+\frac{dx}{dt}Fcosωt\end{eqnarray}$$
このように減衰によるエネルギー減少を示す散逸関数と、周期的外力による項の仕事率で表すことができます。
周期的外力の仕事率について補足しておきますと、
力×距離÷時間で仕事率を表すことができるので、
力は\(Fcosωt\)、距離は\(dx\) (微小な距離)、時間は\(dt\) (微小は時間)と対応させると、周期的外力の仕事率\(w_F\)は下記のようになりますね。
$$w_F=Fcosωt×\frac{dx}{dt}=\frac{dx}{dt}Fcosωt$$
減衰によるエネルギーの計算
減衰によるエネルギー減少分については、上述のように散逸関数\(D\)を用いて\(-2D\)で表すことができますので、下記のようになります。
$$-2D=-cv^2$$
ここで、速度\(v\)を計算しておきます。
変位の式は求められているので、時間微分すれば速度を得ることができますので、変位の式を時間微分しましょう。
まず変位の式は、
$$x(t)=\frac{f}{(ω_0^2-ω^2)^2+4ζ^2ω_0^2ω^2}\{(ω_0^2-ω^2)cosωt+2ζω_0ωsinωt)\}$$
この式を時間微分するのですが、式が煩雑になるので、係数部分を\(A\)とおきます。
$$A=\frac{f}{(ω_0^2-ω^2)^2+4ζ^2ω_0^2ω^2}$$
こうすると、
$$\frac{dx}{dt}=v=Aω\{-(ω_0^2-ω^2)sinωt+2ζω_0ωcosωt)\}$$
求めるものは\(v\)を2乗したものなので、
$$v^2=A^2ω^2\{-(ω_0^2-ω^2)sinωt+2ζω_0ωcosωt)\}^2$$
減衰によるエネルギー減少分を\(w_D\)とすると
$$w_D=-cv^2=-cA^2ω^2\{-(ω_0^2-ω^2)sinωt+2ζω_0ωcosωt)\}^2$$
周期的外力のエネルギー
これは先ほど求めた通り、下記のようなります。
$$w_F=Fcosωt×\frac{dx}{dt}=\frac{dx}{dt}Fcosωt$$
係数の微分の部分は速度\(v\)と同じなので代入すると、
$$w_F=Aω\{-(ω_0^2-ω^2)sinωtFcosωt+2ζω_0ωFcos^2ωt\}$$
このようになります。
1周期分のエネルギーを比較する
減衰によるエネルギーと、周期的外力によるエネルギーが下記のように求まりましたが、このまま比較するのは少し難解になりそうですね。
$$w_D=-cA^2ω^2\{-(ω_0^2-ω^2)sinωt+2ζω_0ωcosωt)\}^2$$
$$w_F=Aω\{-(ω_0^2-ω^2)sinωtFcosωt+2ζω_0ωFcos^2ωt\}$$
複雑に見えるのは三角関数の部分があるからであって、
三角関数を消去すれば見通しがよくなりそうですね。
ということで三角関数を消去するために、積分して1周期分のエネルギーで考えることにします。
周期を\(T\)とすると、
$$T=\frac{2π}{ω}$$
$$\int_0^T w_Ddt=\int_0^T-cA^2ω^2\{-(ω_0^2-ω^2)sinωt+2ζω_0ωcosωt)\}^2dt$$
$$\int_0^T w_Fdt=\int_0^T \{-Aω(ω_0^2-ω^2)sinωtFcosωt+2ζω_0ωFcos^2ωt\}dt$$
このようになって、三角関数部分の積分をしていくわけです。
まず、\(w_D\)の部分ですが、積分の中の2乗部分を展開します。
$$\int_0^T w_Ddt=-cA^2ω^2\int_0^T\{(ω_0^2-ω^2)^2sin^2ωt-2(ω_0^2-ω^2)2ζω_0ωcosωtsinωt+(2ζω_0ω)^2cos^2ωt))\}dt$$
このように書き直すと、三角関数部分の積分は下記3種類の計算をする必要があることがわかります。
$$\begin{eqnarray}\int^T_0cos^2ωtdt&=&\int^T_0\frac{1+cos2ωt}{2}dt\\\\&=&\left[\frac{1}{2}t\right]^T_0+\left[\frac{1}{4}sin2ωt\right]^T_0\\\\&=&\frac{1}{2}T\end{eqnarray}$$
$$\begin{eqnarray}\int^T_0cosωtsinωtdt&=&\int^T_0\frac{1}{2}sin2ωtdt\\\\&=&\left[-\frac{1}{4}cos2ωt\right]^T_0\\\\&=&0\end{eqnarray}$$
$$\begin{eqnarray}\int^T_0sin^2ωtdt&=&\int^T_0\frac{1-cos2ωt}{2}dt\\\\&=&\left[\frac{1}{2}t\right]^T_0-\left[\frac{1}{4}sin2ωt\right]^T_0\\\\&=&\frac{1}{2}T\end{eqnarray}$$
これらを代入すると、
$$\begin{eqnarray}\int_0^T w_Ddt&=&-cA^2ω^2\{(ω_0^2-ω^2)^2\frac{1}{2}T+(4ζ^2ω_0^2ω^2)\frac{1}{2}T\}\\\\&=&-\frac{1}{2}TcA^2ω^2\{(ω_0^2-ω^2)^2+(4ζ^2ω_0^2ω^2)\}\end{eqnarray}$$
\(A\)と\(c\)について、下記のように表されますので、代入します。
$$A=\frac{f}{(ω_0^2-ω^2)^2+4ζ^2ω_0^2ω^2}$$
$$c=2ζ\sqrt{mk}=2ζmω_0$$
代入すると、
$$\begin{eqnarray}\int_0^T w_Ddt&=&-\frac{1}{2}TA2ζmω_0ω^2\frac{f}{(ω_0^2-ω^2)^2+4ζ^2ω_0^2ω^2}\{(ω_0^2-ω^2)^2+(4ζ^2ω_0^2ω^2)\}\\\\&=&-TAζω_0ω^2F\end{eqnarray}$$
次に\(w_F\)の部分を計算します。
$$\begin{eqnarray}\int_0^T w_Fdt&=&\int_0^T \{-Aω(ω_0^2-ω^2)sinωtFcosωt+2ζω_0ωFcos^2ωt\}dt\\\\&=&\frac{1}{2}TA2ζω_0ωF\\\\&=&TAζω_0ω^2\end{eqnarray}$$
よって\(-w_D=w_F\)となり、1周期分のエネルギーの大きさは等しくなります。
つまり、減衰部分で消費されるエネルギーと周期的外力がなすエネルギーが同じになっています。
まとめ
強制振動のエネルギーについて解説しました。
強制振動では減衰で消費されるエネルギーと周期的外力がなすエネルギーが同じであることがポイントですので、
計算は少し大変ですがしっかりと理解しておきましょう。
参考文献
- 振動工学の基礎:岩壺卓三、松久寛、森北出版株式会社
- 機械力学-振動の基礎から制御まで:日高照晃、小田哲、川辺尚志、曽我部雄次、吉田和信、朝倉書店
- 構造と連続体の力学基礎:熊でもわかる変形できる物体の力学:岩熊哲夫、小山茂 web版
初心者向けの振動工学の教科書・参考書をこちらで紹介していますので、参考にしていただければと思います。
本サイトの振動工学のページはこちら。