ひずみってぼや~っと理解できてはいるんだけど、テストとか問題解けないんだよね・・・


高校物理では基本的に変位量を考えていたけど、ひずみは変位した割合を示しているんだ。
本日はについて解説します。
高校物理では、『ひずみ』という単語が出てこなくて、大学に入って急に出てきて、なんじゃこりゃ??ってなった人も多いと思います。
アニメーションを使ってわかりやすく解説しますので、ひずみのイメージを頭に叩き込みましょう。
本記事をおススメする人
- ひずみがよくわからない人
- 材料力学、構造力学が苦手な人
ひずみについてはこちらの動画でも解説していますので、参考にしていただければと思います。
ポアソン比についてはこちらの動画を参考にしてください。
ひずみ(Strain)の定義

ひずみとは、力がかかった時に 元の大きさに対してどれだけ変化したか、を示します。
ポイントは『 元の大きさに対して』という点です。
具体的には冒頭の図で示すとおりです。
長さの変化量を元の長さで割りますので、単位は無次元になります。
変化の比率を示していますので、無次元になることも理解できますね。
(1割とか10%とか、割合と同じ感覚でOKです。)
ひずみの種類
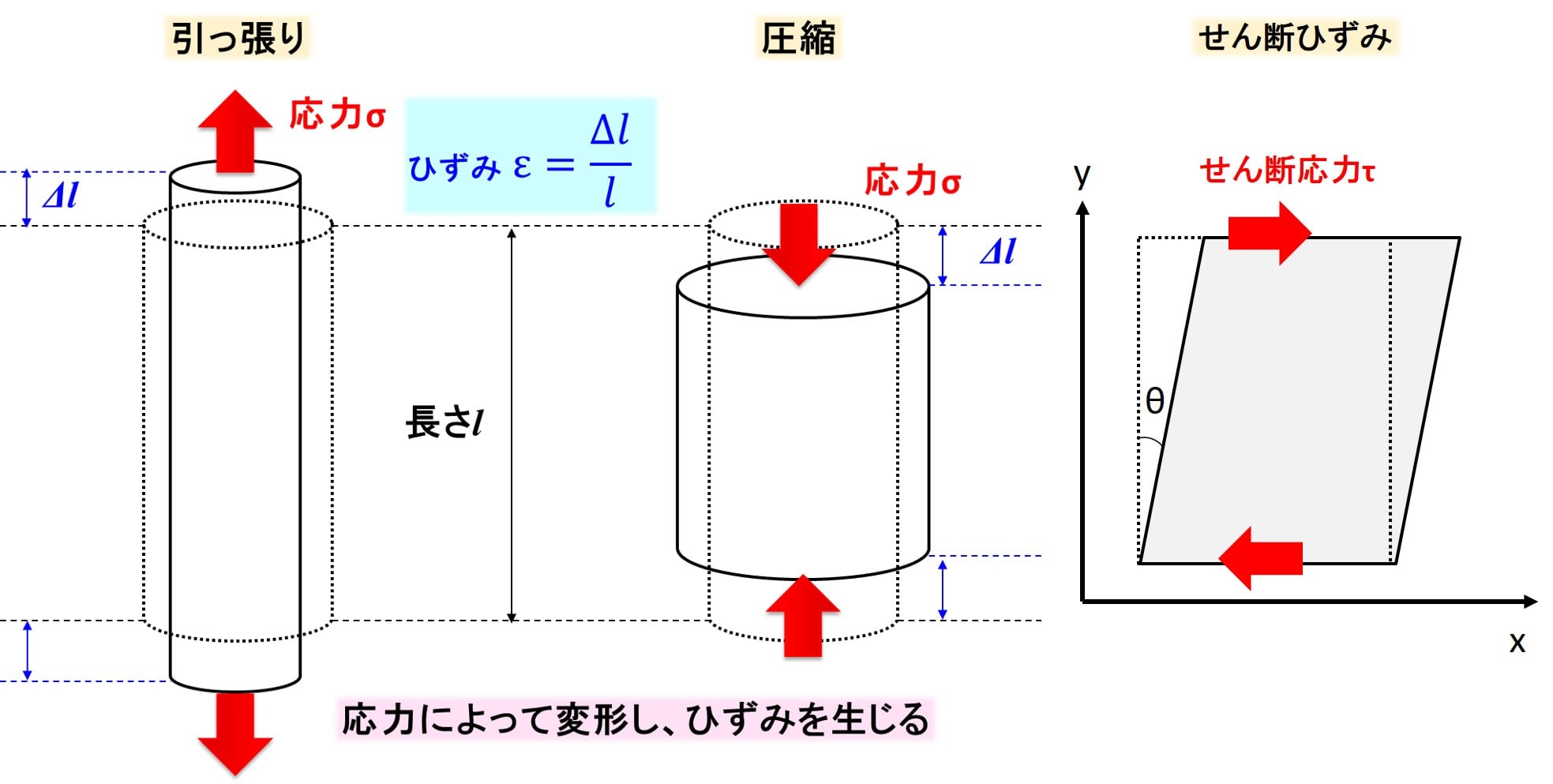
垂直方向のひずみとせん断方向のひずみの2種類です。
垂直方向のひずみには2種類あり、引張と圧縮の二つで、全部で引っ張り、圧縮、せん断の3つとなります。
それぞれを解説していきます。
垂直ひずみ(Normal Strain)
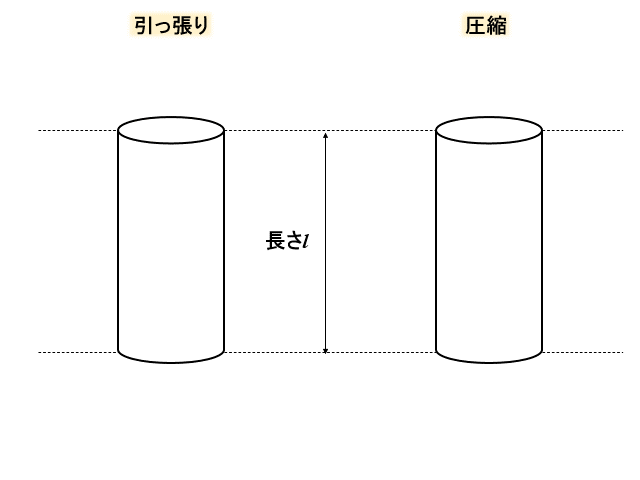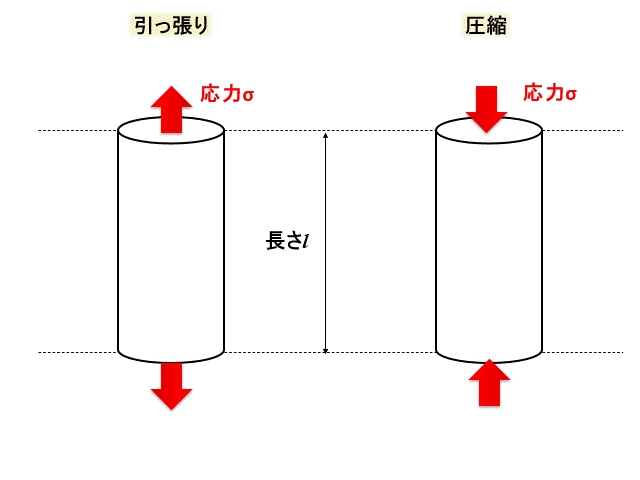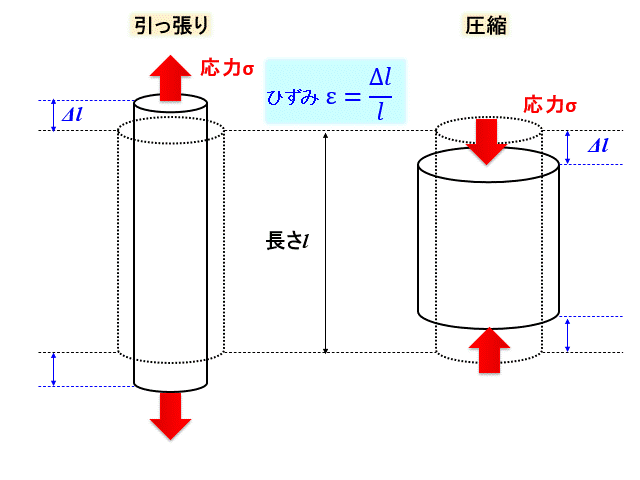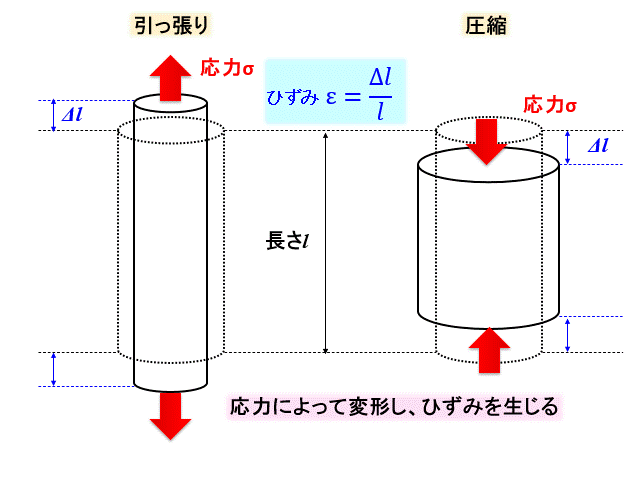
上記のような応力とひずみの関係性のとき、垂直ひずみとなります。
応力、ひずみの方向が、 物体を引っ張る方向であれば、引っ張り応力と引っ張りひずみです。
逆に 物体を圧縮する方向であれば、圧縮応力と圧縮ひずみと呼んでいます。
ポアソン比
ポアソン比は 物体を引っ張ったときに、引っ張った方向と垂直方向に変形する比率を示したものです。
垂直方向??なんかよくわからん・・・


それじゃあ、具体的にアニメーションを見てみようか。
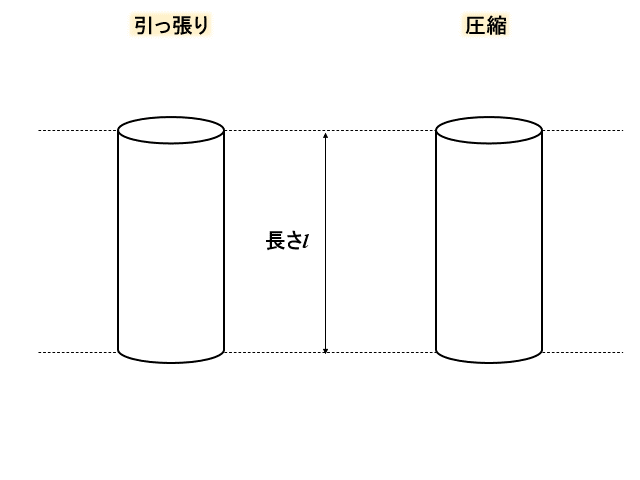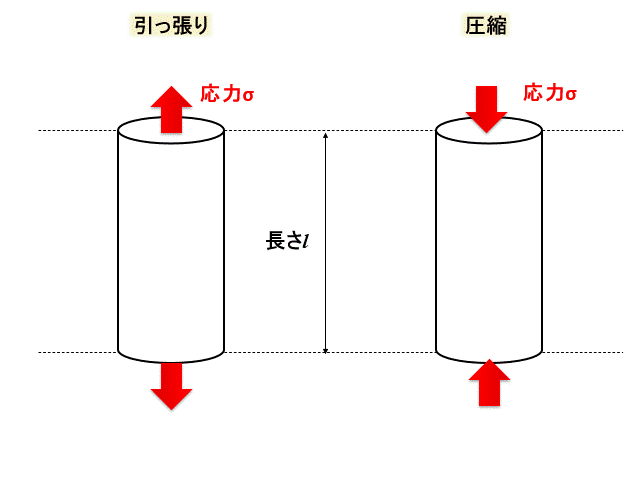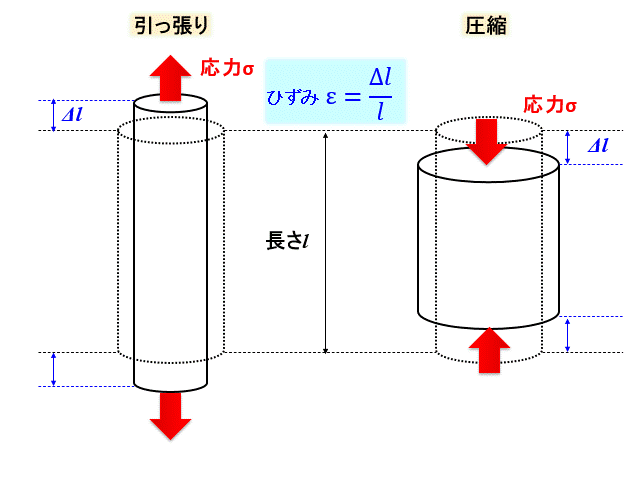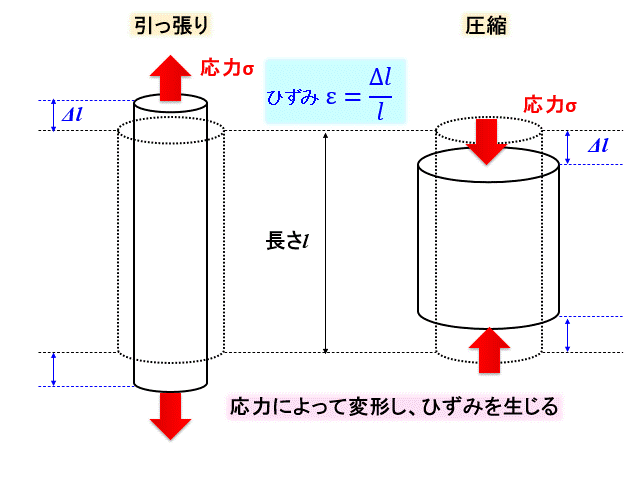
図の左側のように棒を縦に引っ張ったら、物体は横方向に縮みますね。
逆に圧縮応力を加えたらどうなるでしょう?
図の右側のように、横方向には伸びて太くなりますね。
応力をかける方向のひずみをε、応力をかける方向と垂直方向のひずみをε'とすると
ポアソン比ν(ギリシャ文字で"ニュー")は、
$$ν=\frac{ε'}{ε}$$
ポアソン比は応力をかけた時に、応力をかけた方向のひずみに対して 応力と垂直な方向に発生するひずみの比率を示しています。
せん断ひずみ(Shearing Strain)
せん断ひずみは、物体をゆがませる方向のひずみで、ギリシャ文字でγ(ガンマ)を用いて表します。
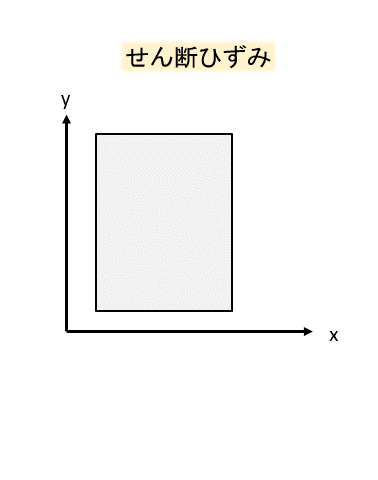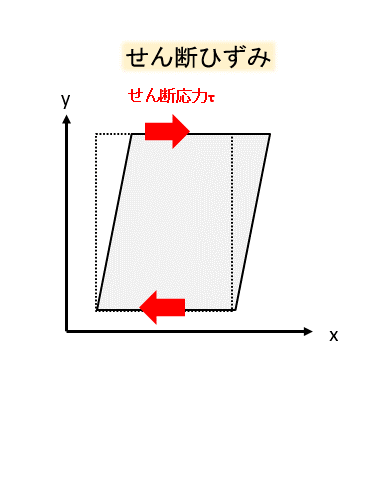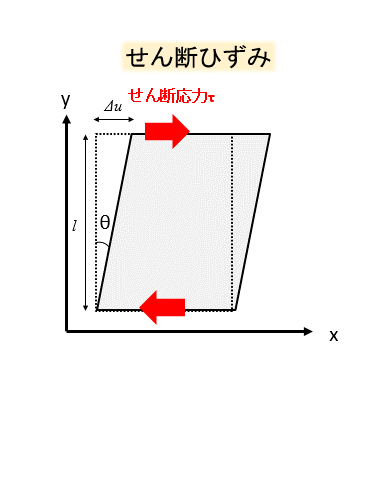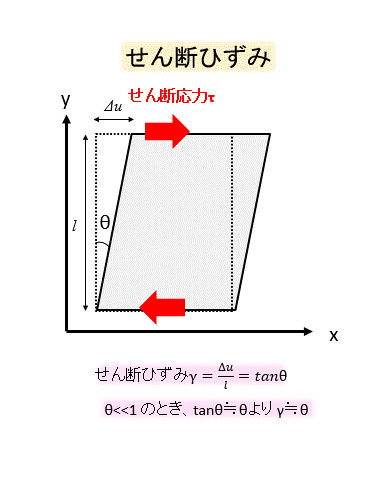
面に水平な方向にPの力が作用したとき、物体はこのように水平方向にゆがみますね。
正方形の断面は平行四辺形のようになります。
このときのゆがみの程度をせん断ひずみと呼んでいます。
ひずみに関わる重要な公式
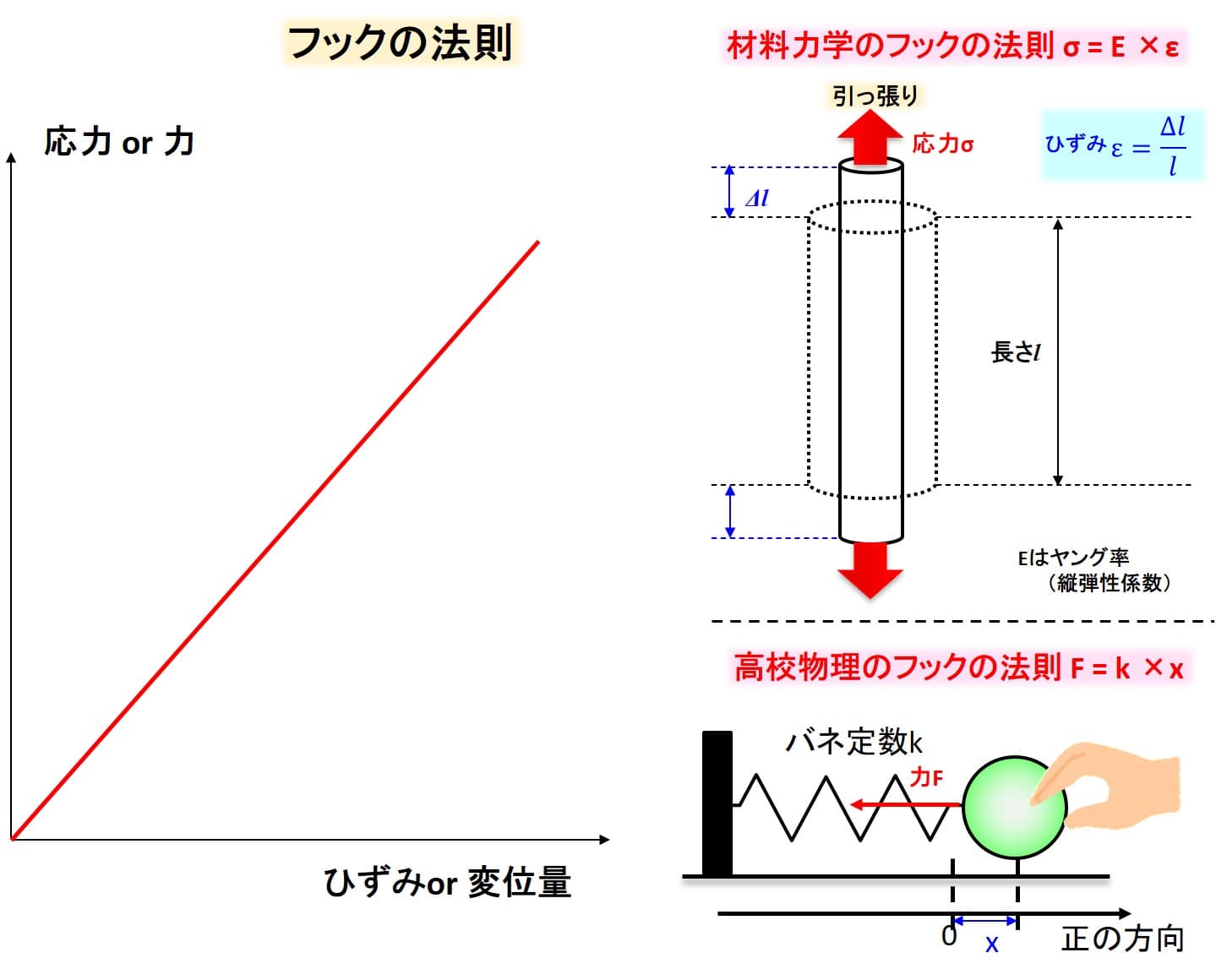
これは応力とひずみの関係式である、フックの法則が非常に重要になります。
応力とフックの法則に関しては過去の記事で解説していますので、参考にしてください。
簡単に解説すると、 応力はひずみの大きさに比例する、という法則です。
ただし、材料によって、比例関係が成立するひずみ量は決まっていますので注意してください。
ひずみとポアソン比のまとめ
ひずみとポアソン比について解説しました。
ひずみは応力をかけたときに、元の大きさにどれだけ変化したかを示す量です。
ポアソン比は、圧縮や引張の応力をかけたときに、応力をかけた方向と垂直方向に伸び縮みする度合いを示します。
縦に置いた棒を縦に引き延ばしたら薄くなりますよね。
あるいは棒を縦方向から圧縮したら太ります。
ポアソン比はそんなイメージです。
最後に、ひずみに関する重要な公式として、フックの法則を紹介しました。
基礎的な法則になりますので、過去記事を参考にマスターしておきましょうね。
初心者向けの参考書・教科書をこちらで紹介していますので、書籍選びに迷っている方は参考にしていただければと思います。
参考文献
- 現代材料力学:渋谷寿一、本間寛臣、斎藤憲司、朝倉書店
- 基礎材料力学[改訂版]:小泉堯(監修)、笠野英秋, 原利昭, 水口義久、養賢堂
- 材料力学 第3版:黒木剛司郎、森北出版株式会社
初心者向けの教科書・参考書はこちら
材料力学の記事一覧はこちら
次の記事→材料力学 応力-ひずみ曲線と塑性変形、弾性変形をわかりやすく解説