振動・波動の基礎-⑪2自由度系の非減衰強制振動の一般解

2自由度の強制振動って特解だけ見てたけど、一般解は見なくてもいいの？

苦手君

デルタ先生

実際の波形は一般解の形になるから、一般解の形を見ておくべきだけど、共振とか反共振点の議論をするだけだったら、特殊解だけで議論しても大丈夫なことが多いよ。

本記事では、2自由度の非減衰の強制振動の一般解の波形について解説します。

前回は強制振動の特解を求めて、その波形について解説しました。

今回はさらにリアルな振動として、一般解がどのようになっているのか、グラフからイメージできるようになりましょう。

本記事をおススメする人

2自由度の強制振動を理解したい人
物理を勉強していて興味がある人、仕事で振動の知識を使う人

下記動画でも解説していますので、参考にしていただければと思います。

2自由度の非減衰強制振動

モデルと運動方程式

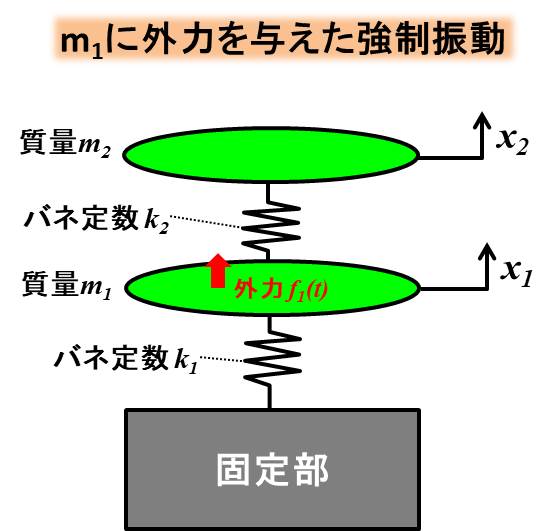
今回取り扱うモデルです。

運動方程式は下記のようになります。

$$m_1\ddot{x_1}+(k_1+k_2)x_1-k_2x_2=Fcosωt$$

$$m_2\ddot{x_2}-k_2x_1+k_2x_2=0$$

2自由度の非減衰強制振動の一般解

前回、解き方のところで解説しましたが、非斉次微分方程式が連立した式を解く必要があり、その一般解というのは、

一般解=斉次方程式の一般解+非斉次方程式の特解

という形で、 斉次方程式の一般解は自由振動のときの一般解になるのでした。

自由振動のケースは下記の過去記事を参考にしてください。

参考記事

自由振動の一般解の復習

自由振動の復習ですが、1次の固有振動モードにおける質点$m_1、m_2$の振幅をそれぞれ、$u_1\color{red}{^1}$、$u_2\color{red}{^1}$、

2次の固有振動モードにおける質点$m_1、m_2$の振幅をそれぞれ

$u_1\color{green}{^2}、u_2\color{green}{^2}$と置くと、自由振動の一般解は、

$$\left(\begin{array}{c}x_1(t)\\x_2(t)\end{array}\right)=A\left(\begin{array}{c}u_1\color{red}{^1}\\u_2\color{red}{^1}\end{array}\right)cosω\color{red}{_1}\color{black}t+B\left(\begin{array}{c}u_1\color{green}{^2}\\u_2\color{green}{^2}\end{array}\right)cosω\color{green}{_2}\color{black}t+C\left(\begin{array}{c}u_1\color{red}{^1}\\u_2\color{red}{^1}\end{array}\right)sinω\color{red}{_1}\color{black}t+D\left(\begin{array}{c}u_1\color{green}{^2}\\u_2\color{green}{^2}\end{array}\right)sinω\color{green}{_2}\color{black}t・・・①$$

この式の微分形と、位置と速度のt=0の初期条件$x_{10}、x_{20}、v_{10}、v_{20}$から係数の$A、B、C、D$を求めることができます（三角関数の$sin$の項はゼロになり、$cos$の項だけ残りますね）。

$u$に関する文字を簡単にするために、下記のように振幅比$A_1$と$A_2$を導入します。

$\color{red}{ω_1}$の時の$u_1、u_2$を$u_1\color{red}{^1}$、$u_2\color{red}{^1}$とし、$\frac{u_2\color{red}{^1}}{\color{black}{u_1}\color{red}{^1}}\color{black}=\color{red}{A_1}$、

$\color{green}{ω_2}$の時の$u_1、u_2$を$u_1\color{green}{^2}、u_2\color{green}{^2}$とし、$\frac{u_2\color{green}{^2}}{\color{black}{u_1}\color{green}{^2}}\color{black}=\color{green}{A_2}$とします。

そして、下記のように振幅の前の係数を置きなおします。

$$A'=Au_1\color{red}{^1}$$

$$B'=Bu_2\color{green}{^2}$$

$$C'=Cu_1\color{red}{^1}$$

$$D'=Du_2\color{green}{^2}$$

このように置くと、係数は下記のように求まります。

$$A'=\frac{-A_2x_{10}+x_{20}}{A_1-A_2}・・・②$$

$$B'=\frac{A_1x_{10}-x_{20}}{A_1-A_2}・・・③$$

$$C'=\frac{-A_2v_{10}+v_{20}}{(A_1-A_2)ω_1}・・・④$$

$$D'=\frac{A_1v_{10}-v_{20}}{(A_1-A_2)ω_2}・・・⑤$$

強制振動の特解の復習

特解は前回、導出しています。

今回は質点$m_1$に周期的な外力を与えたとします。

特殊解を下記のように設定します。

$$x_1=X_1cosωt、x_2=X_2cosωt・・・⑥$$

注意すべきは、ここの与える力の振動数のωは既知の値ということです。

振幅は前回の結果から、下記のようになります。

$$X_1=\frac{(-m_2ω^2+k_2)F}{m_1m_2(ω^2-ω_1^2)(ω^2-ω^2_2)}・・・⑦$$

$$X_2=\frac{k_2F}{m_1m_2(ω^2-ω_1^2)(ω^2-ω^2_2)}・・・⑧$$

強制振動の一般解

一般解の形は、自由振動の一般解と強制振動の特解の和で求まりますので、①と⑥式の和になりますね。

ではこのグラフを見てみましょう。

実際に計算する際に値を入れないといけませんので、$m_1、m_2、k_1、k_2、F$は全て1とし、初期条件として$x_{20=1}$として、他の初期条件はゼロにします。

この時、$ω_1～0.618、ω_2～1.618$、反共振点は1となります。

まず、$ω=0.1$のときのグラフを見てみましょうか。

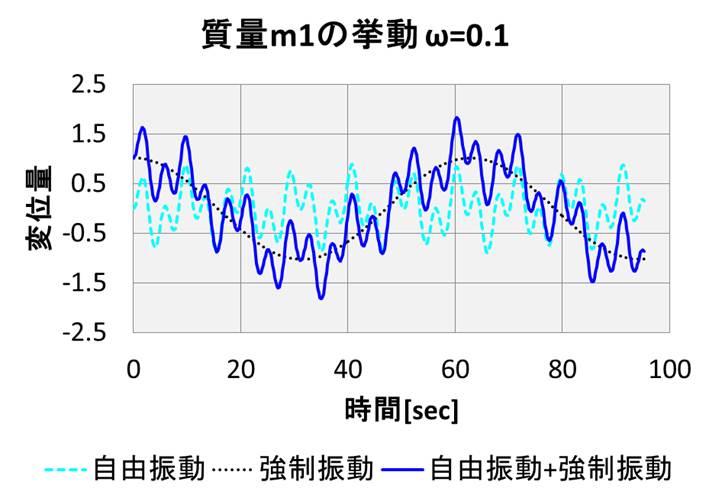
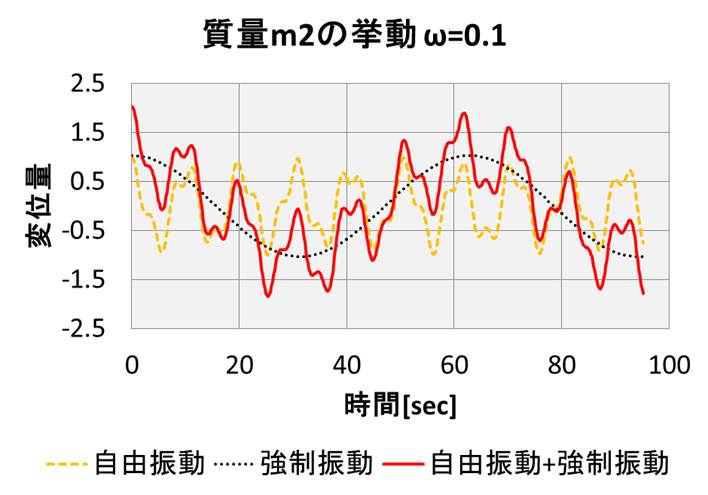
青が質量$m_１$の変位の時間変化、赤が質量$m_2$の変位の時間変化を示しています。

実線が、強制振動の一般解、点線は自由振動の一般解で、黒点線は強制振動の特解です。

強制振動の一般解は、点線同士の足し算で描かれていますね。

それでは、各振動数のときの波形をアニメーションで見てみましょう。

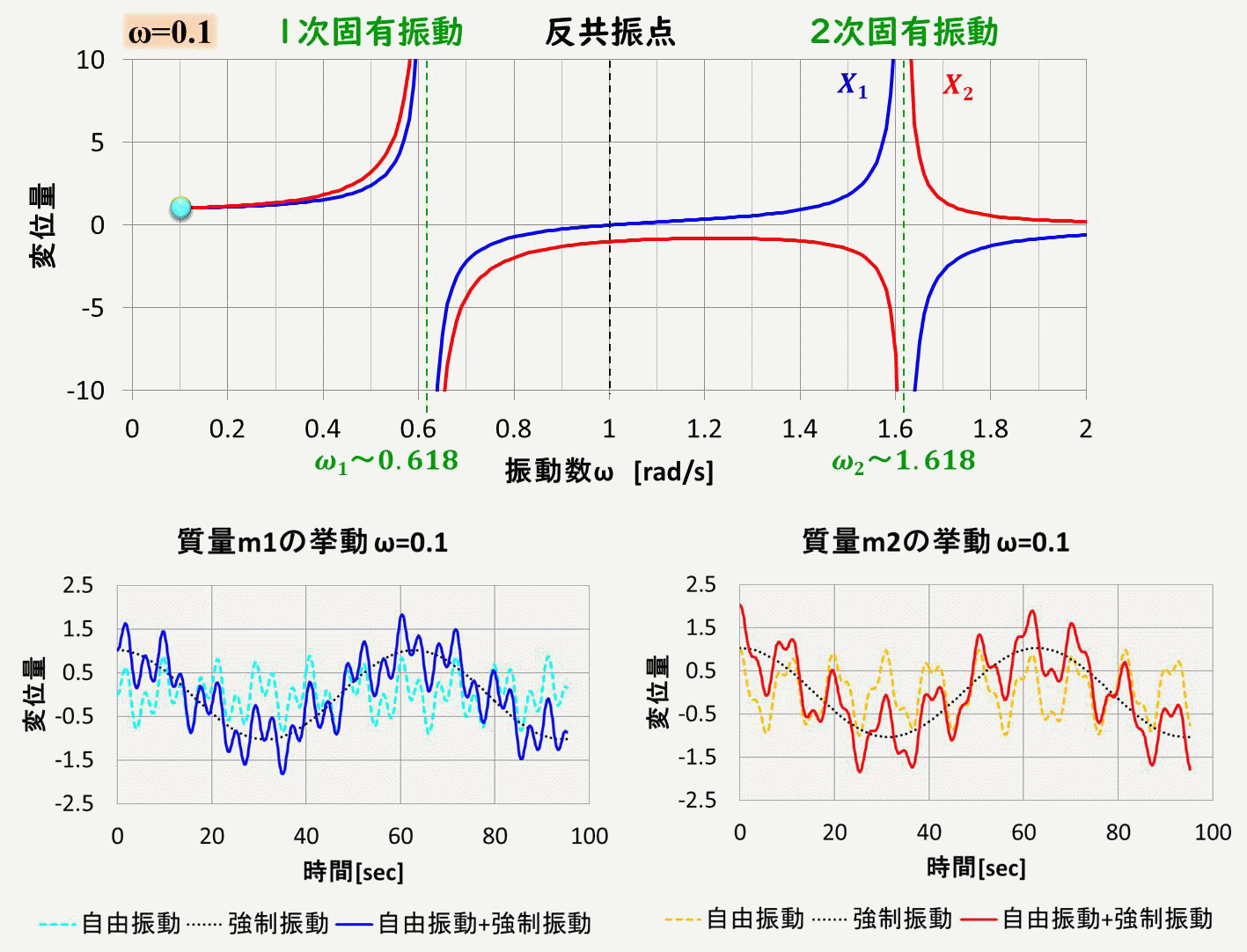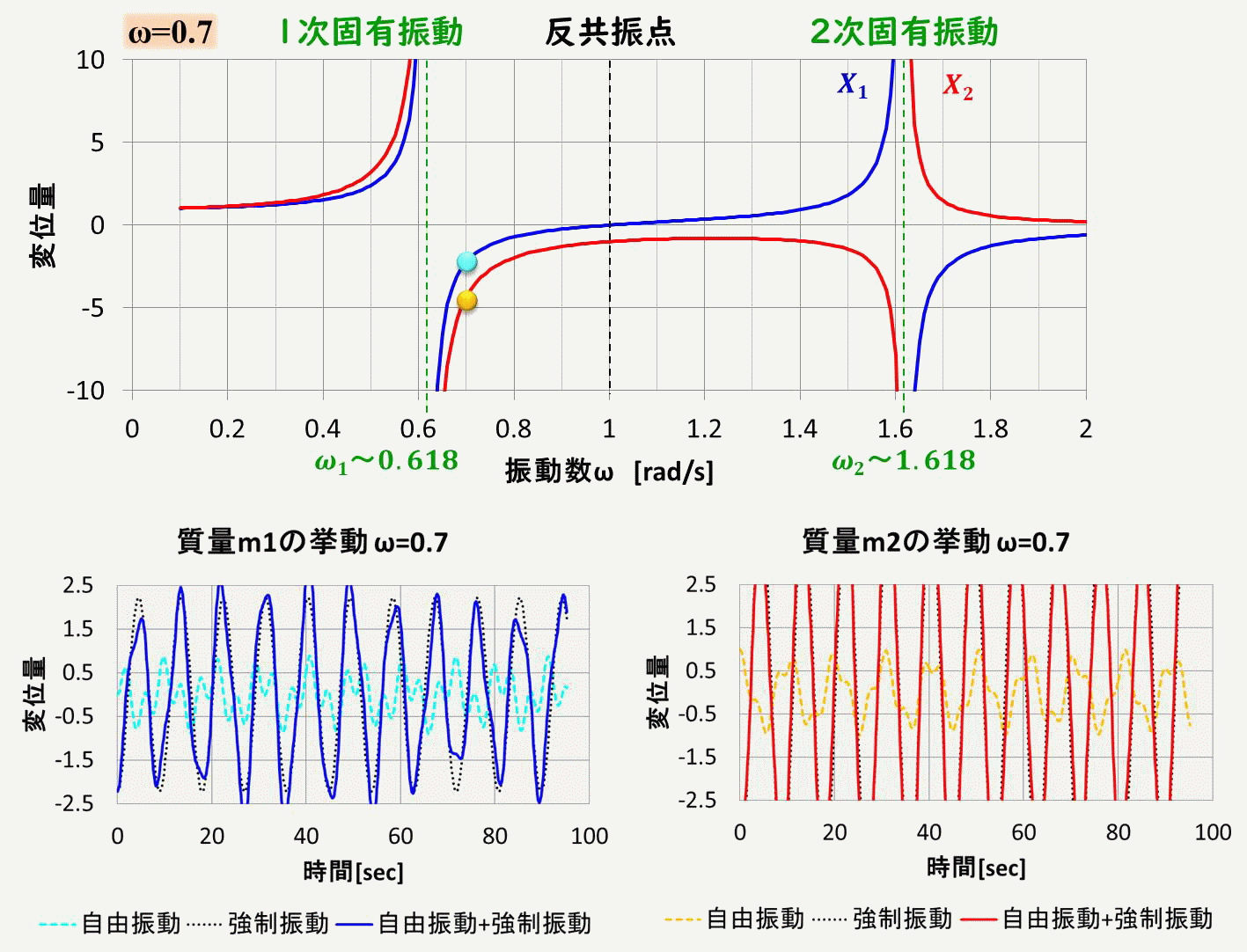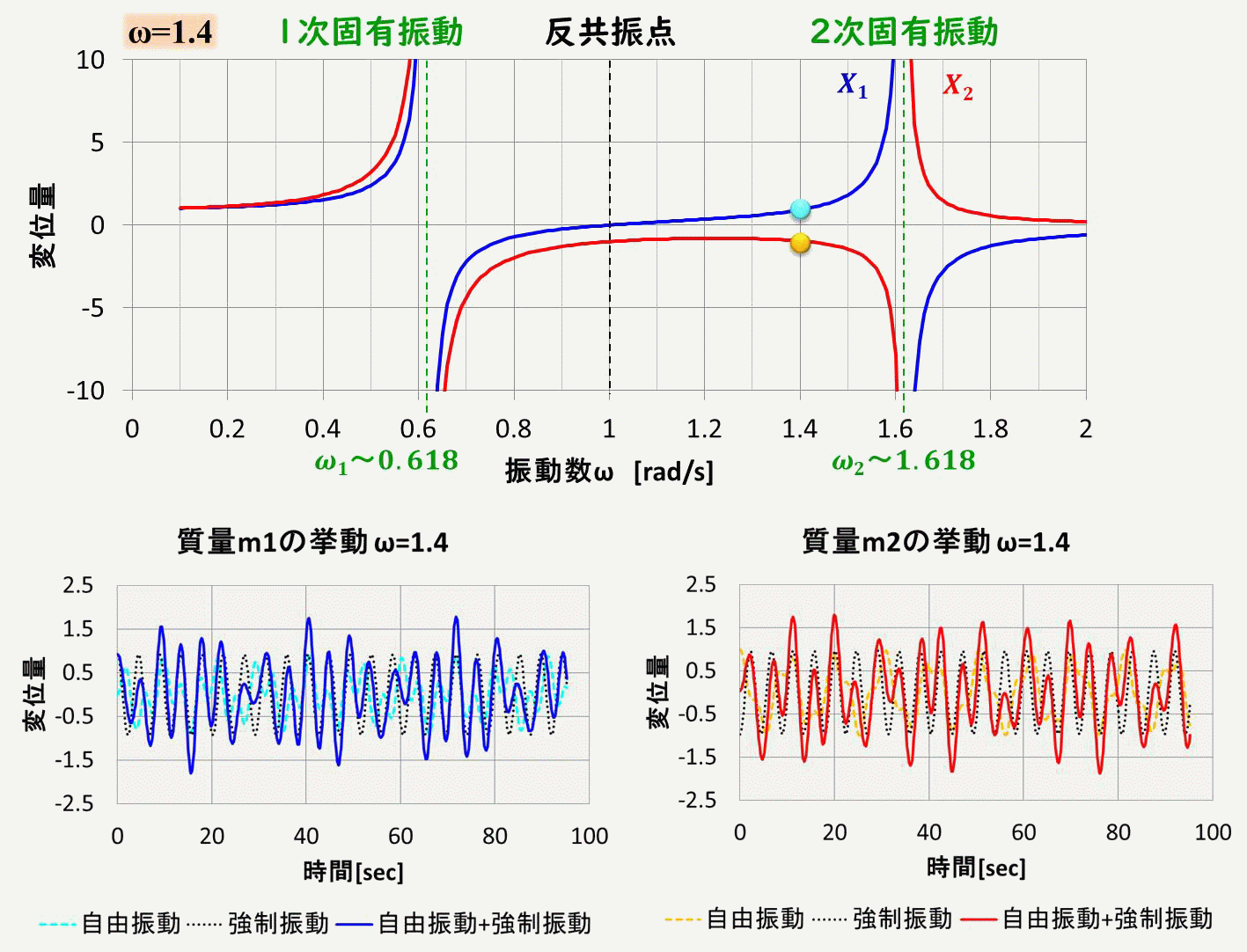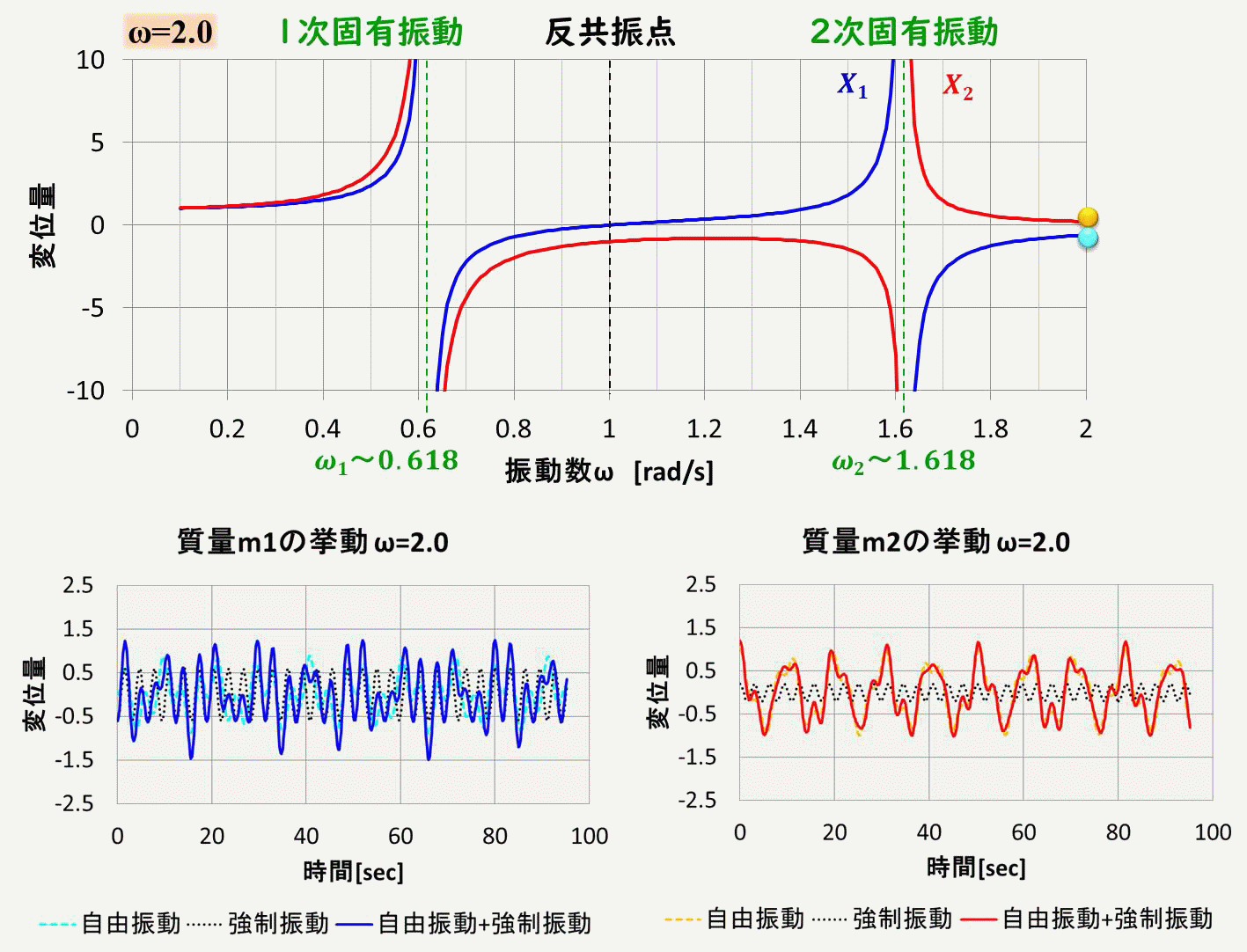
さて、このアニメーションですが、上側のグラフは、強制振動の特解から求めた、振幅の振動数依存性を示しています。

下側のグラフは質量m1（青色）と質量m2（赤色）の変位量の時間変化です。

実線は強制振動の一般解で、自由振動の一般解（点線）と強制振動の特解（黒点線）を示しています。

共振点では、強制振動の特解の値が大きくなっていることが分かると思います。

共振点付近では、自由振動の影響が非常に小さいとして議論することが多いわけですね。

ちなみにこの強制振動の周波数を変化させたアニメーションですが、実際の振動試験でも似たような試験をしています。

周波数スイープ試験というものがあり、これは 加える外力の周波数を徐々に変化させていく試験であり、共振点を探すためによく使われます。

この周波数スイープ試験というものが、まさにこのアニメーションでやっていることに近いですので、この波形のイメージを持つと、試験内容の理解が深まりますよ。

まとめ

2自由度の非減衰強制振動の一般解を解説しました。

大切なことは、共振点付近では、自由振動の成分は小さくなり、強制振動の成分が共振することで強く出る、ということです。

アニメーションの波形イメージをもつことで、理解が深まりますので、頭に焼き付けてくださいね。

参考文献

振動工学の基礎：岩壺卓三、松久寛、森北出版株式会社
機械力学-振動の基礎から制御まで：日高照晃、小田哲、川辺尚志、曽我部雄次、吉田和信、朝倉書店
構造と連続体の力学基礎：熊でもわかる変形できる物体の力学：岩熊哲夫、小山茂 web版

初心者向けの振動工学の教科書・参考書をこちらで紹介していますので、参考にしていただければと思います。

初心者向けの教科書・参考書はこちら

振動工学の記事一覧はこちら

次の記事 → 振動・波動の基礎-⑩2自由度系の非減衰強制振動と反共振点