2自由度の振動って動吸振器のモデルだけ勉強しておけばいいの?


代表的なものは、まだいくつかあるんだけど、その中でもよく出てくる連成振動については勉強しておいた方がよいね。
今回は、2自由度のモデルでよく出てくる『連成振動』について解説します。
本記事をおススメする人
- 2自由度の振動を勉強している人
- 物理を勉強していて興味がある人、仕事で振動の知識を使う人
動画でも解説していますので、参考にしていただければと思います。
2自由度の連成振動について
2自由度の連成振動をそのまま使うことは少ないです。
しかし3自由度以上の多自由度へ拡張すると、いろいろなモデルへ展開できますので、しっかり学んでおきましょう。
では、連成振動とはどんなモデルなのか?
百聞は一見に如かず、モデルを見てみましょう。
連成振動のモデル
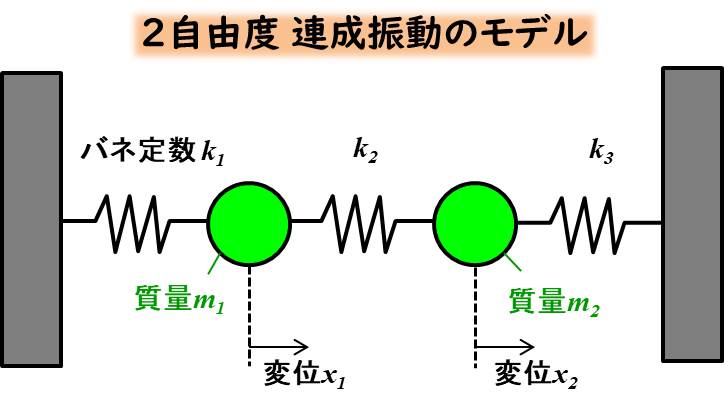
質点がバネに繋がれており、両側の壁にも繋がれている状態です。
動吸振器のモデルを過去の記事で解説していましたが、動吸振器は片側にしか壁が無いようなモデルでしたね。
運動方程式から一般解を導く
さて、運動方程式を立てるわけですが、今回は一番簡単な例として、バネ定数がすべて同じで、2つの質量も同じ場合を考えましょう。
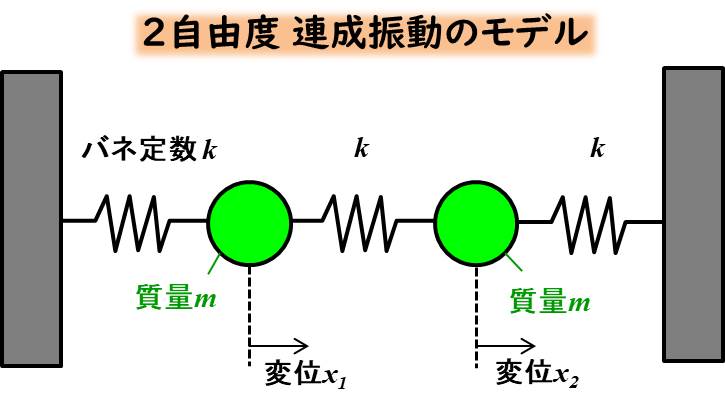
このような図になりますね。
バネ定数がすべてkです。
質点に作用する力
運動方程式は、左側の質点と右側の質点の2つを作ることができますので、まず左側の質点について考えてみましょう。
左側の質点にかかる力を図で示すと下記にようになります。
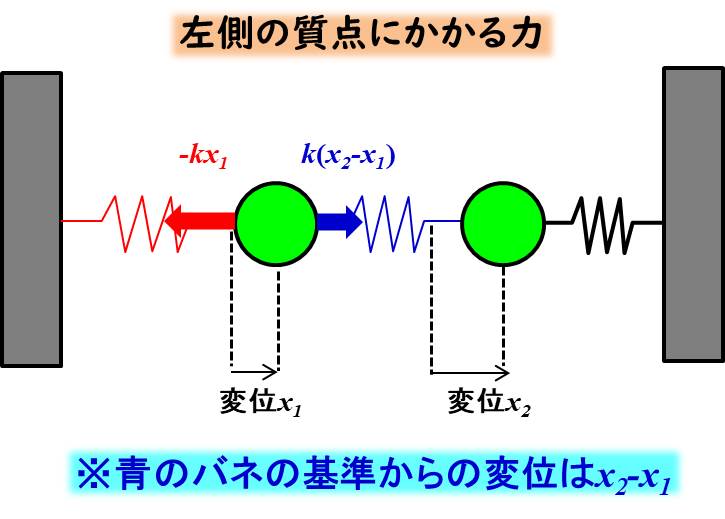
変位する方向を正としていることに注意してください。
左側の赤のバネから受ける力は、\(-kx_1\)、真ん中の青のバネから受ける力は\(k(x_2-x_1)\)となります。
青のバネの基準からの変位が、左側の質点の変位と右側の質点の変位の差\(x_2-x_1\)になりますね。
符号がごっちゃになる方は、 どちらかの質点だけ動かしてみて、質点のかかる力の向きが正の方向かどうかを確認してみましょう。
例えば、\(x_2=0\)として、左側の質点を正の方向に動かしてみましょう。
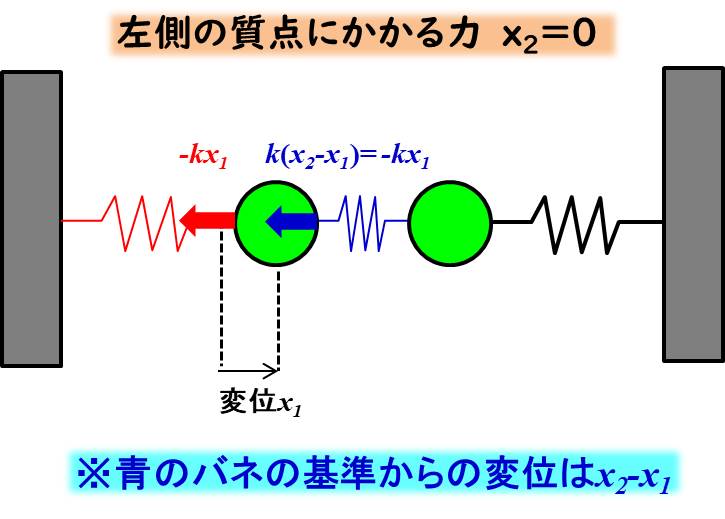
青のバネは絶対に縮みます。
縮んだバネは左側の質点を押し返そうとしますので、負の方向、つまり図の左側の方向に力を発生させます。
このイメージと式があっているかを確認します。
青のバネからの力は、\(k(x_2-x_1)\)で、この式に\(x_2=0\)を代入すると、\(-kx_1\)となってマイナスがついた式になりますので、符号はこれでOKですね。
では、次に右側の質点にかかる力を見てみましょう。
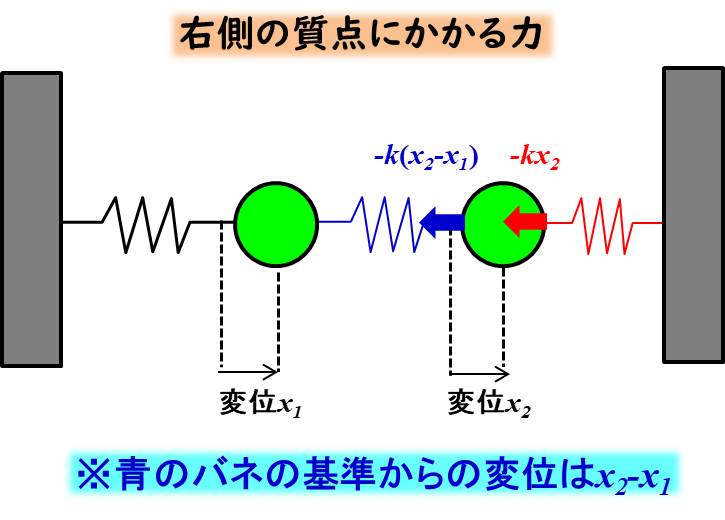
今回は赤のバネを右側にしています。
赤のバネの復元力を考えると、\(x_2\)の方向と逆方向になります。
これは$x_2$を正の方向に動かすと、必ず赤のバネは縮むことになりますので、質点を押し返そうとして、負の方向に復元力が発生しますね。
よって、赤色のバネからの復元力は\(-kx_2\)となります。
青色のバネからの力ですが、作用・反作用の法則を考えましょう。
すると、左側の質点に作用する力を考えた時の力と反対方向にするだけですので、\(-k(x_2-x_1)\)ですね。
運動方程式
以上、質点に作用する力が求まりましたので、運動方程式を書いてみましょう。
左側の質点に関しての運動方程式は、
右側の質点に関しての運動方程式は、
①と②式の両辺をmで割って、角振動数\(ω_0=\sqrt{\frac{k}{m}}\)を使って書き換え整理しましょう。
この連立微分方程式を解けばよいわけですが、今回は式も簡単なので、複素数を使わず、三角関数を使って解いてみましょう。
特殊解を導出
ちなみに、こちらの過去の記事でも2自由度の振動系について同じ解き方を行っていますので、参考にしてください。
特殊解を\(x_1=A_1cosωt、x_2=A_2cosωt\)と置くと、それぞれの2回微分は、
$$\ddot{x_1}=-ω^2A_1cosωt$$
$$\ddot{x_2}=-ω^2A_2cosωt$$
③、④の\(x_1、x_2\)に代入すると、\(cosωt\)が消去できるので、③、④式は下記のように整理できます。
$$(ω^2-2ω_0^2)A_1+ω_0^2A_2=0・・・⑤$$
$$ω_0^2A_1+(ω^2-2ω_0^2)A_2=0・・・⑥$$
行列で書くと下記のようになります。
この連立方程式が、\(A_1=A_2=0\)以外の解をもつためには、 1次従属である必要があり、係数の行列式がゼロとならなければなりません。
線形代数の内容ですね。
行列式は、下記のようになります。
整理すると、
$$(ω^2-2ω_0^2)^2-ω_0^4=0$$
因数分解しますと、
$$(ω^2-3ω_0^2)(ω^2-ω_0^2)=0$$
ωは実数なので、この式を満たすようなωは\(ω=\sqrt{3}ω_0、ω_0\)となります。
これらが固有振動モードの角振動数で、小さい方の\(ω_0\)を1次の固有振動モード、大きい方の\(\sqrt{3}ω_0\)を2次の固有振動モードと呼びます。
さて、\(A_1、A_2\)は1次従属の関係にあるので、個別の振幅は求まらず、\(A_1\)と\(A_2\)の振幅比が求まります。
1次の固有振動のときの振幅比を求めるために、⑤式に\(ω=ω_0\)を代入してみますと、
$$-ω_0^2A_1+ω_0^2A_2=0$$
\(ω_0^2\)を消去できますので、\(A_1=A_2\)となります。
同様に2次の固有振動の振幅比は⑤式に\(ω=\sqrt{3}ω_0\)を代入して、
$$ω_0^2A_1+ω_0^2A_2=0$$
これも\(ω_0^2\)を消去できますので、\(A_1=-A_2\)となります。
1次の固有振動は2つの質点が同じ方向に、 2次の固有振動は2つの振動が逆方向に動く、ということがわかります。
これらの特殊解の線形結合を書くと、
一般解の導出
最後に、今回は\(cosωt\)を解として、解きましたが、\(sinωt\)の解もくっつけて一般解となりますので、\(sin\)でも解きましょう。
と言っても、\(cos\)のときとまったく同じ要領で解けます。
\(x_1=B_1sinωt、x_2=B_2sinωt\)として、③、④式に代入すると、\(sin\)が消去できて、⑤、⑥と同じ形式の式が出てきます。
\(sin\)のときの特殊解も\(cos\)の特殊解といっしょに線形結合で表記したものが一般解ですので、下記のようになります。
$$\left(\begin{array}{c}x_1\\x_2\end{array}\right)=A\left(\begin{array}{c}1\\1\end{array}\right)cosω_0t+B\left(\begin{array}{c}1\\-1\end{array}\right)cos\sqrt{3}ω_0t+C\left(\begin{array}{c}1\\1\end{array}\right)sinω_0t+D\left(\begin{array}{c}1\\-1\end{array}\right)sin\sqrt{3}ω_0t・・・⑦$$
\(A,B,C,D\)は定数で、初期条件から求まる値となります。
初期条件として、\(x_1、x_2\)の初期変位をそれぞれ\(x_{10}、x_{20}\)、初期速度を\(v_{10}、v_{20}\)とします。
⑦の両辺を時間で微分して、速度の式を作り出すと、
$$\left(\begin{array}{c}\dot{x_1}\\\dot{x_2}\end{array}\right)=ω_0(-A\left(\begin{array}{c}1\\1\end{array}\right)sinω_0t-\sqrt{3}B\left(\begin{array}{c}1\\-1\end{array}\right)sin\sqrt{3}ω_0t+C\left(\begin{array}{c}1\\1\end{array}\right)cosω_0t+\sqrt{3}D\left(\begin{array}{c}1\\-1\end{array}\right)cos\sqrt{3}ω_0t)・・・⑧$$
⑦式と⑧式に\(t=0、x_1=x_{10}、x_2=x_{20}、\dot{x_1}=v_{10}、\dot{x_2}=v_{20}\)を代入すると、
$$x_{10}=A+B$$
$$x_{20}=A-B$$
$$v_{10}=ω0(C+\sqrt{3}D)$$
$$v_{20}=ω0(C-\sqrt{3}D)$$
これらから、\(A、B、C、D\)を求めると下記のようになります。
$$A=\frac{x_{10}+x_{20}}{2}$$
$$B=\frac{x_{10}-x_{20}}{2}$$
$$C=\frac{v_{10}+v_{20}}{2ω_0}$$
$$D=\frac{v_{10}-v_{20}}{2\sqrt{3}ω_0}$$
自由振動のグラフ
それでは初期条件を入力して、グラフを見てみましょう。
初期条件として、\(x_1、x_2\)の初期変位を\(x_{10}=1、x_{20}=0\)、初期速度を\(v_{10}=v_{20}=0\)とします。
また、バネ定数と質量は全て1とします。
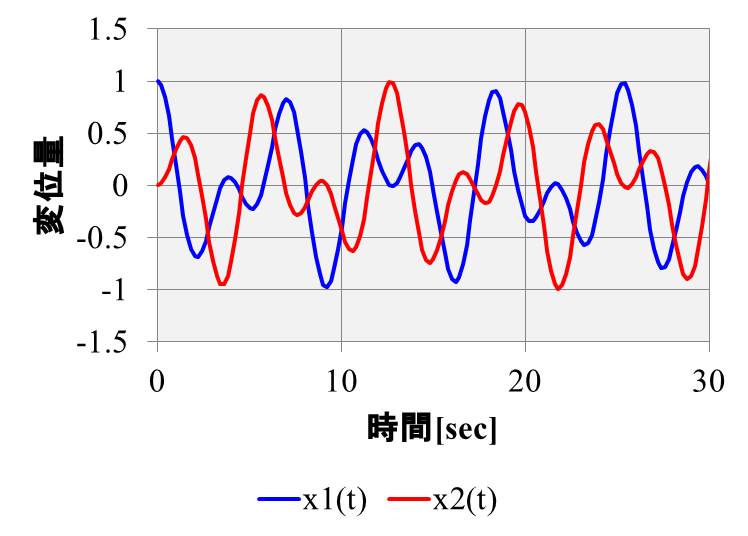
青が左側の質点、赤が右側の質点の変位です。
個別のグラフを見てみると、左側の質点の変位は、下のグラフになります。
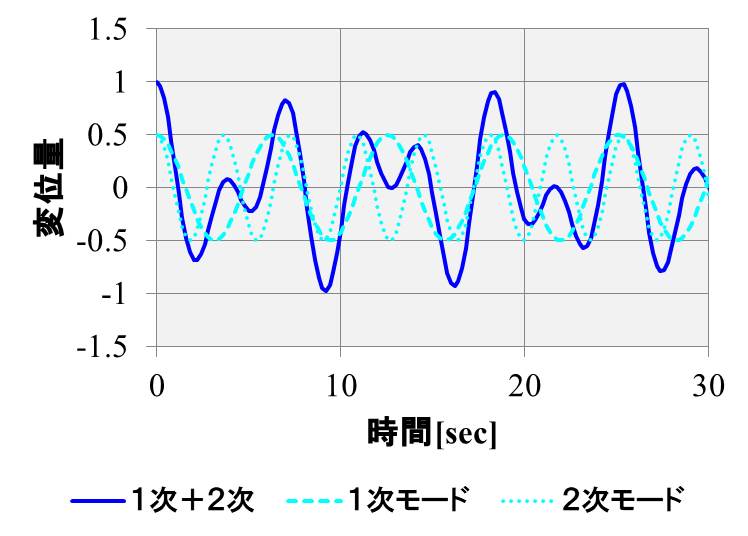
青の実線が、自由振動のときの変位、水色の点線が1次、2次モードの成分で、点線の成分を足し合わせると、青の実線になります。
右側の質点の変位は下図のようになります。
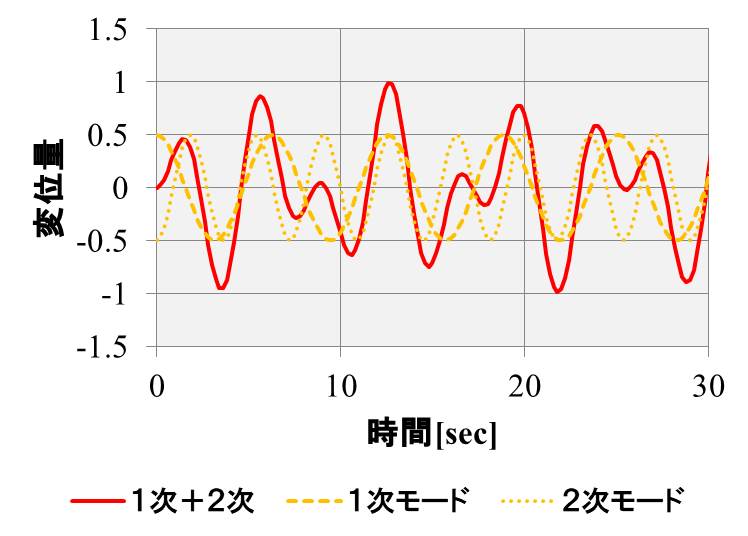
赤の実線が、自由振動のときの変位、オレンジ色の点線が1次、2次モードの成分で、点線の成分を足し合わせると、赤の実線になります。
では、具体的にどのような動きをするかをアニメーションで見てみましょう。
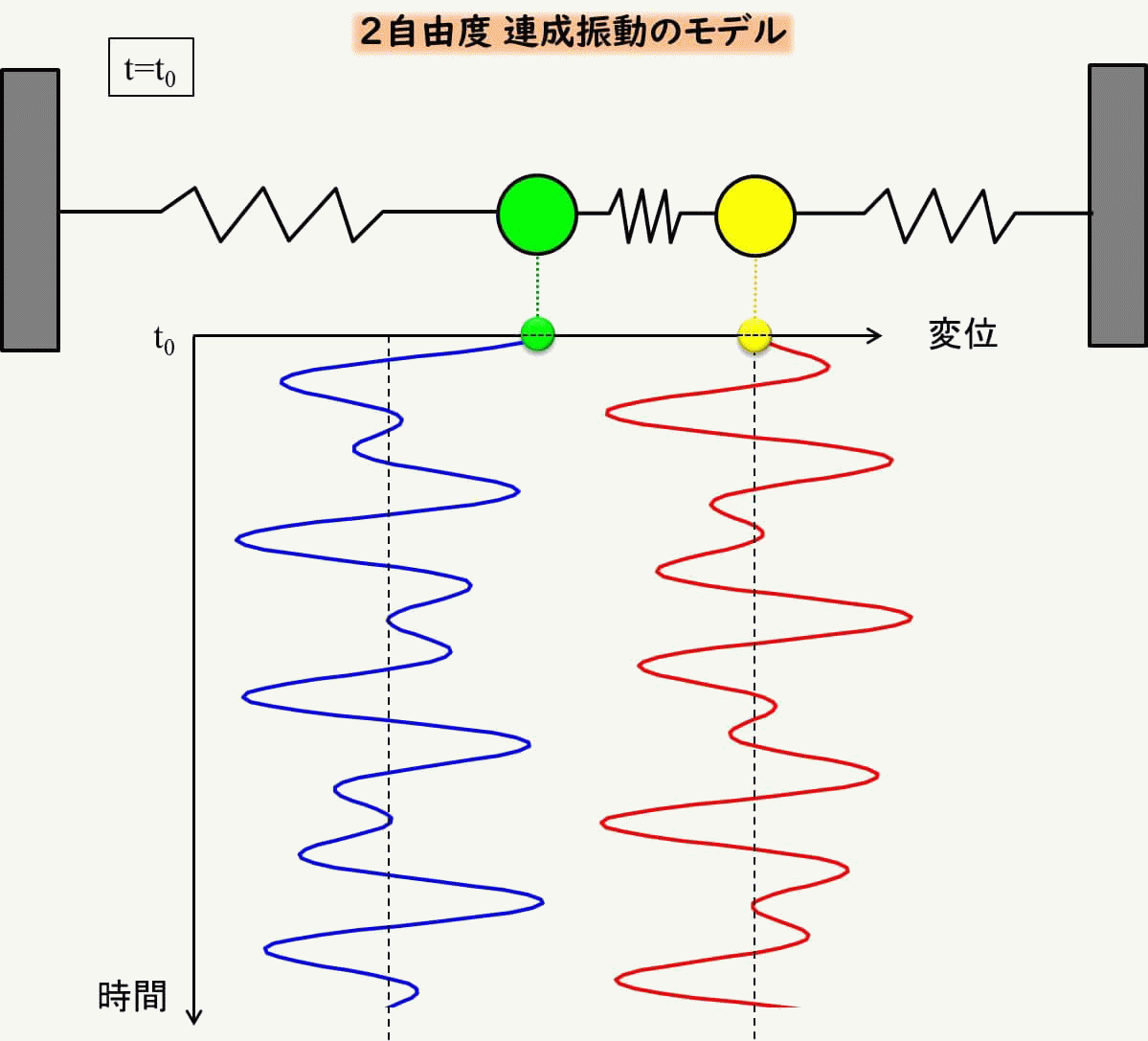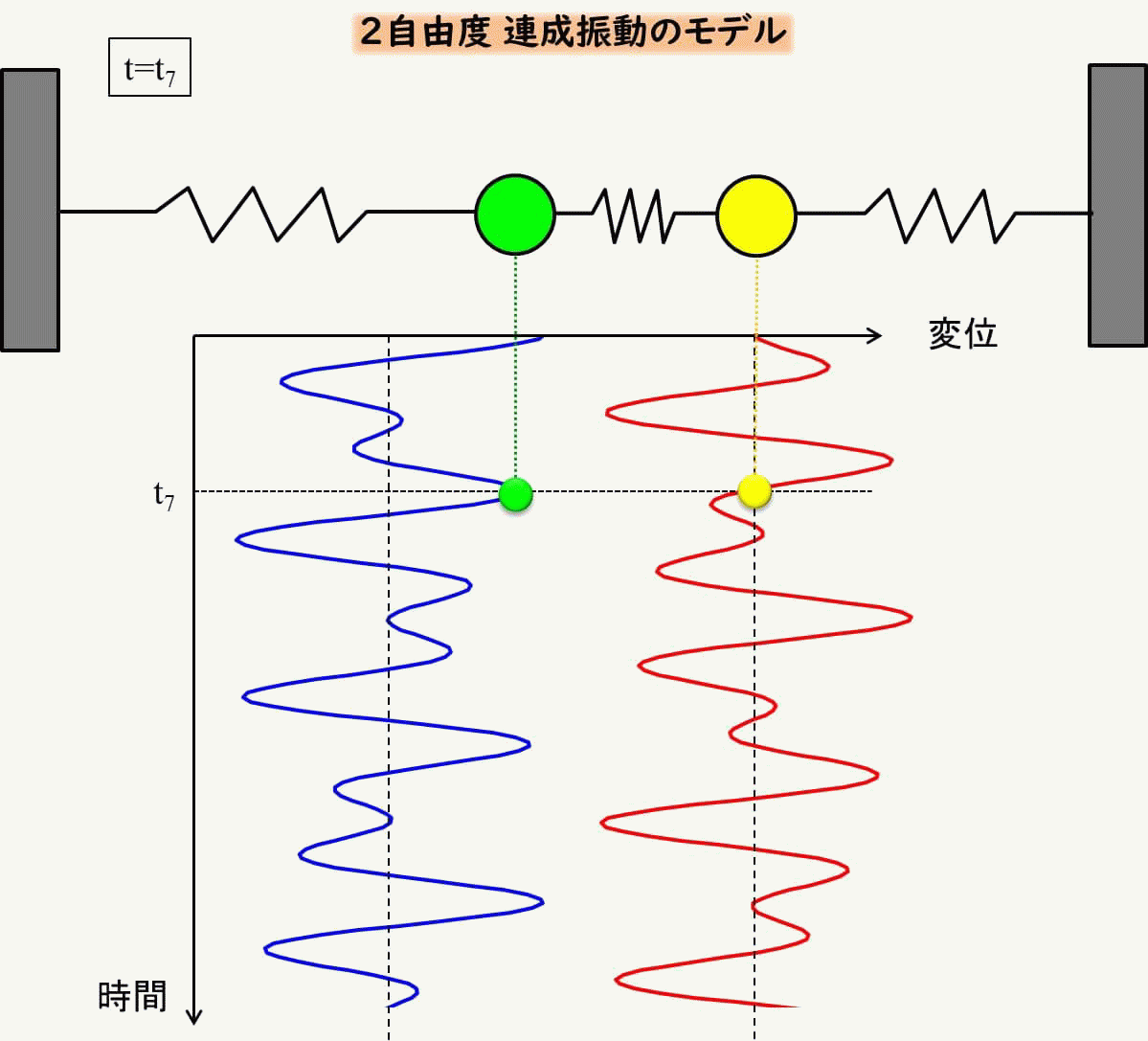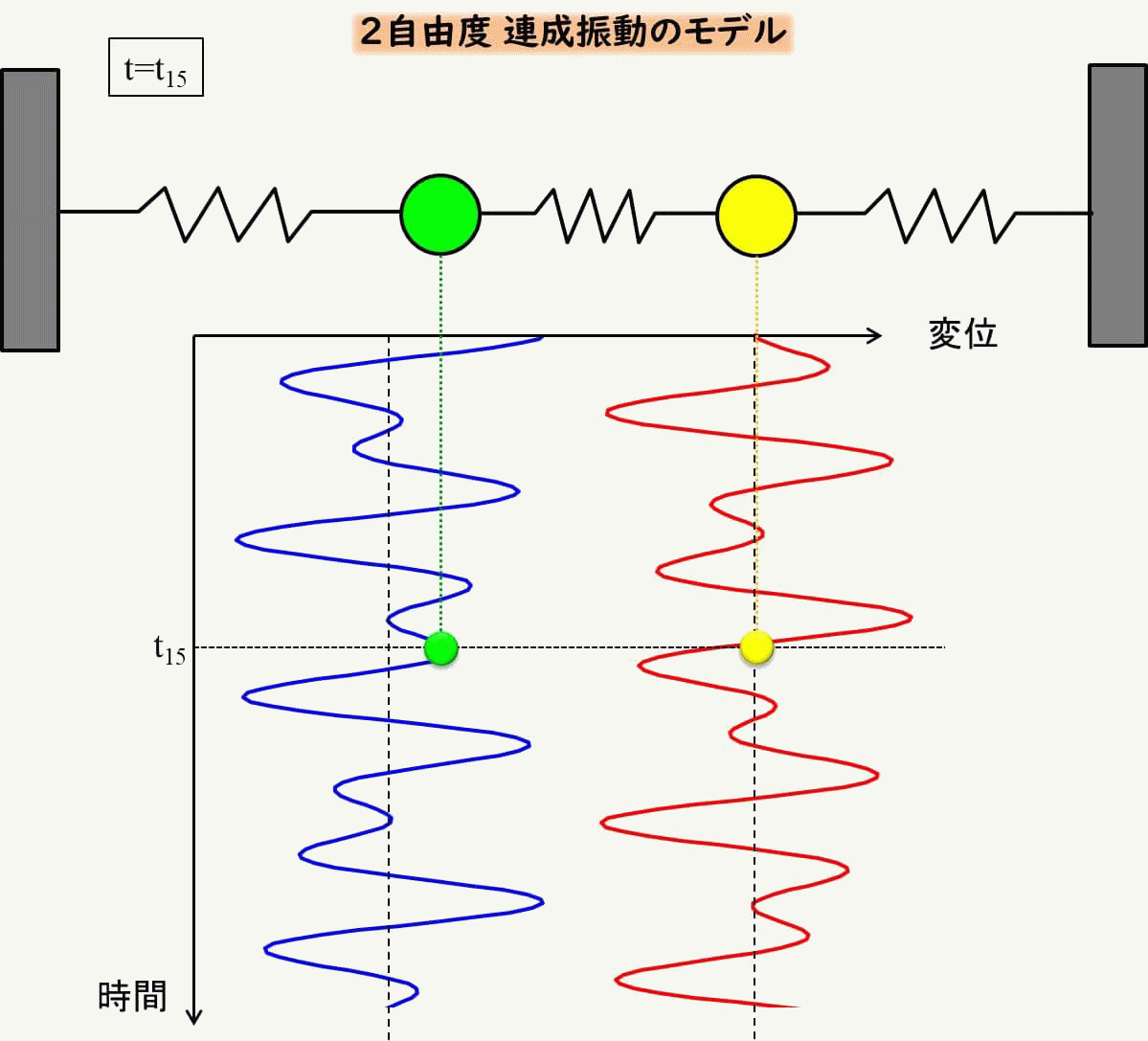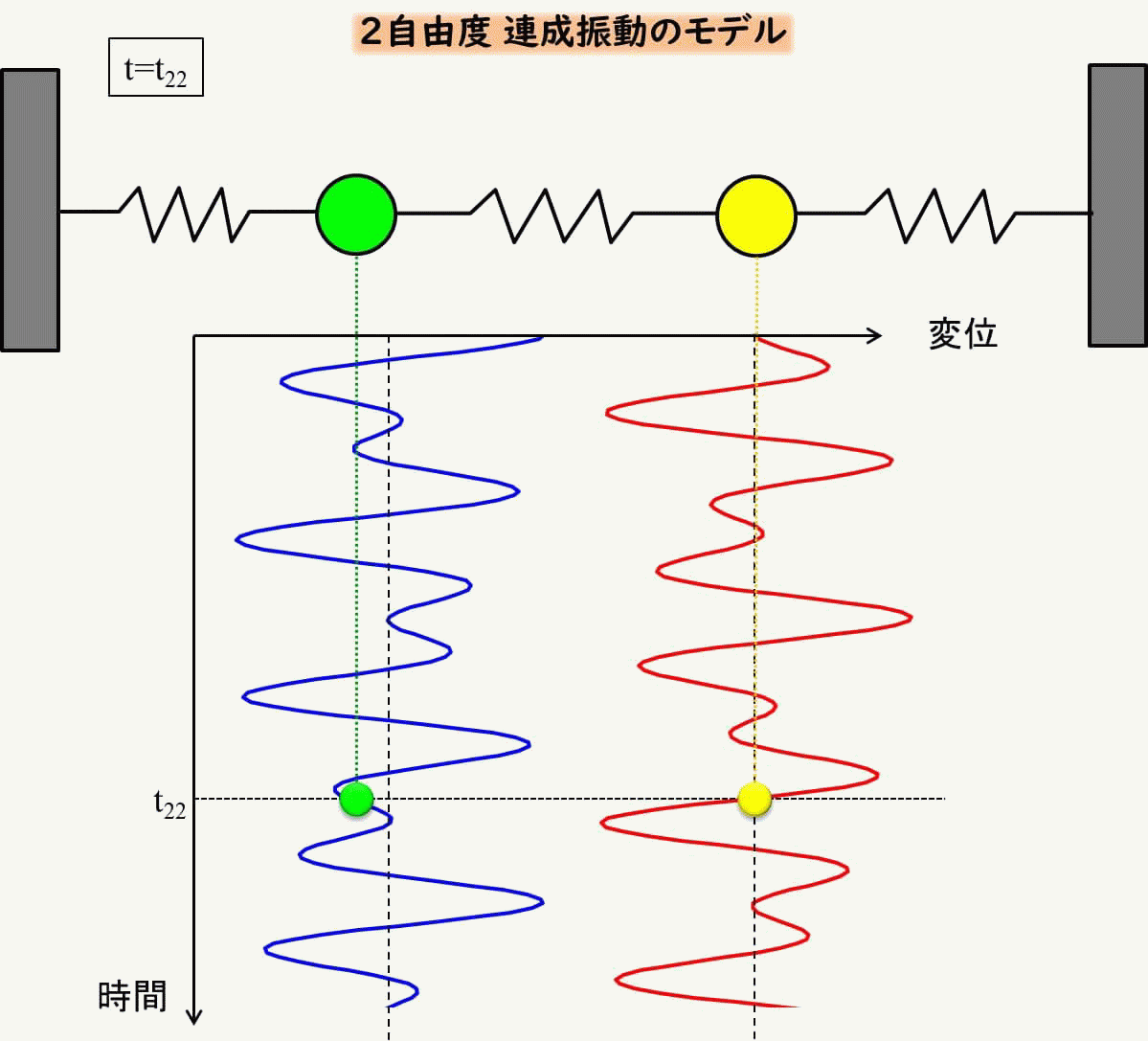
なんとも複雑ですね。
こんな風になるんだ、と思っていただくだけでOKです。
1次モードのみの初期条件
1次モードのみの振動にする場合の初期条件を考えてみましょう。
$$\left(\begin{array}{c}x_1\\x_2\end{array}\right)=A\left(\begin{array}{c}1\\1\end{array}\right)cosω_0t+B\left(\begin{array}{c}1\\-1\end{array}\right)cos\sqrt{3}ω_0t+C\left(\begin{array}{c}1\\1\end{array}\right)sinω_0t+D\left(\begin{array}{c}1\\-1\end{array}\right)sin\sqrt{3}ω_0t・・・⑦$$
⑦式の2次モードに関わる成分の係数を0にするように、初期条件を決めてあげればよいわけです。
2次モードに関わる成分の係数はBとDですね。
\(B\)と\(D\)は下記のようになっています。
$$B=\frac{x_{10}-x_{20}}{2}$$
$$D=\frac{v_{10}-v_{20}}{2\sqrt{3}ω_0}$$
これらが0になるように初期条件を設定します。
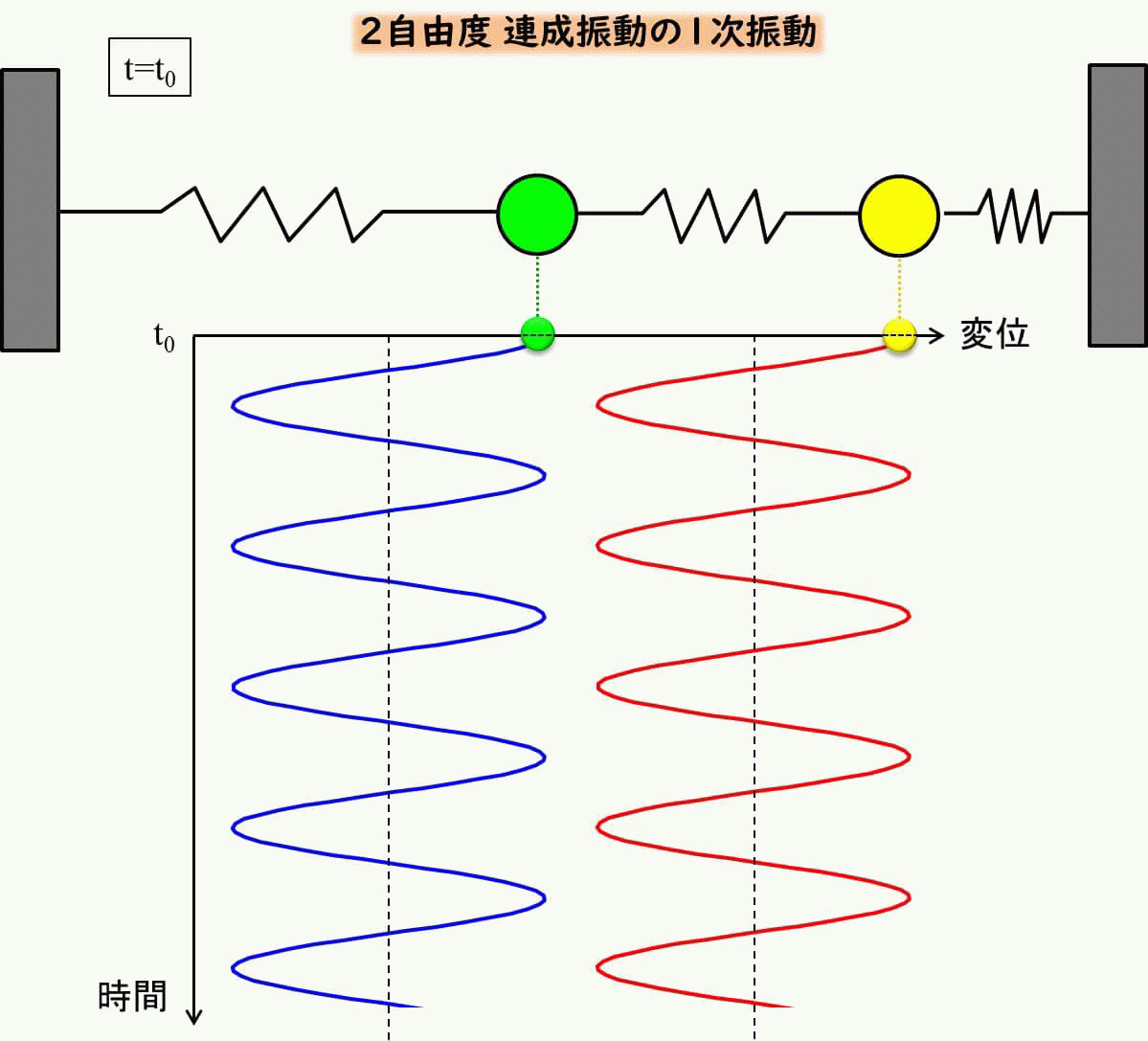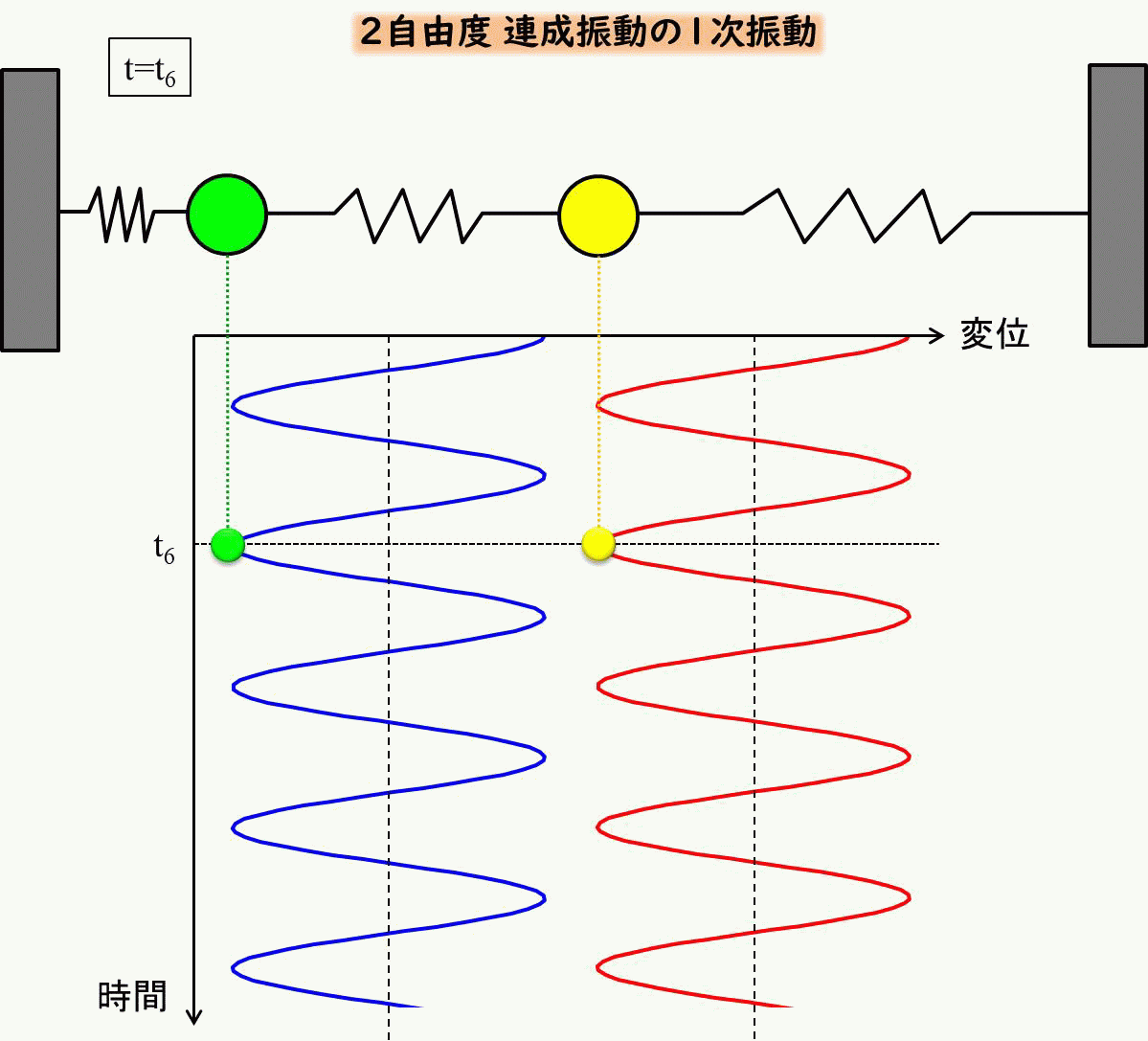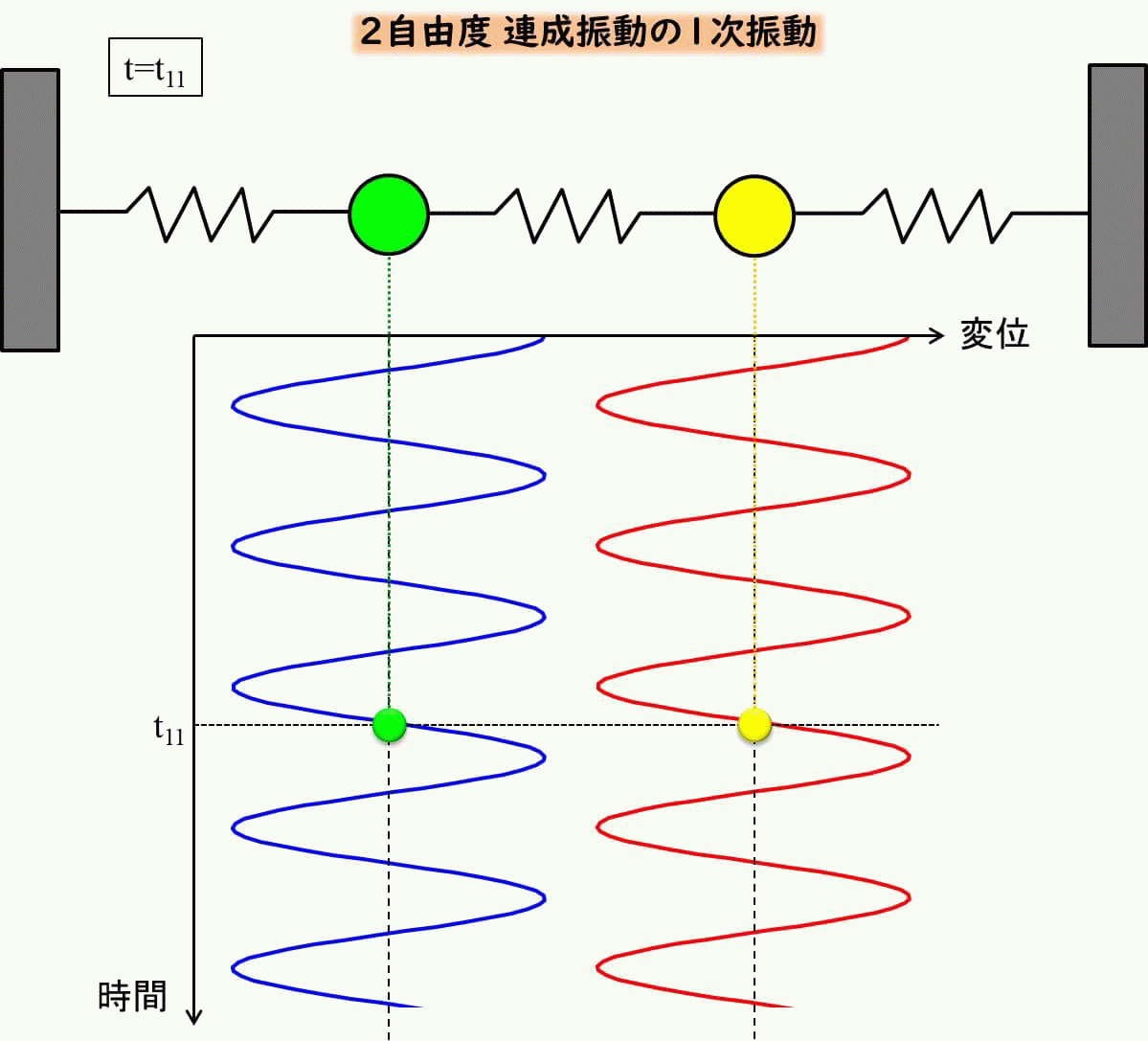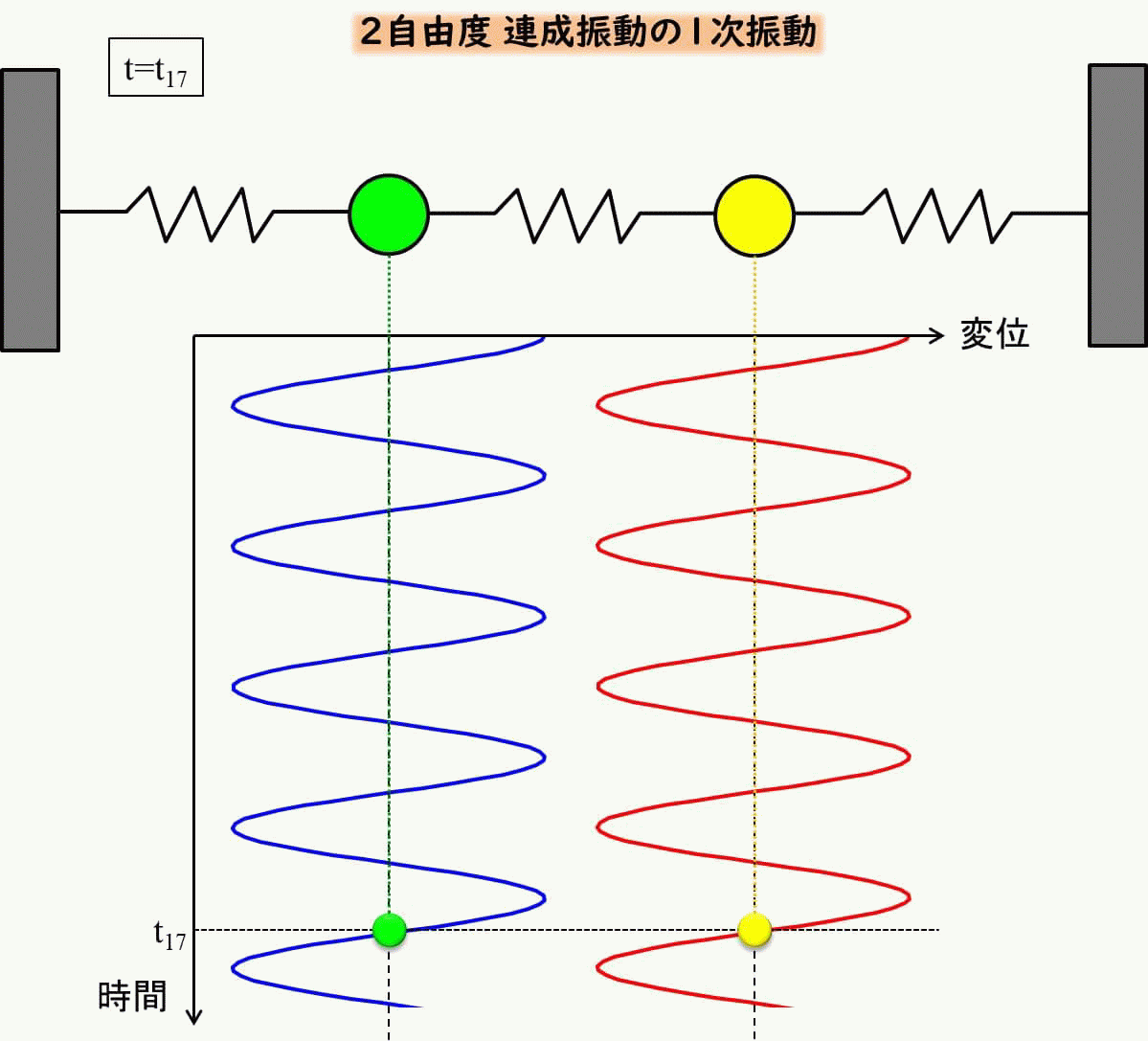
\(x_1、x_2\)の初期変位を\(x_{10}=x_{20}=1\)、初期速度を\(v_{10}=v_{20}=0\)としましょう。
すると、グラフは下記のようになります。
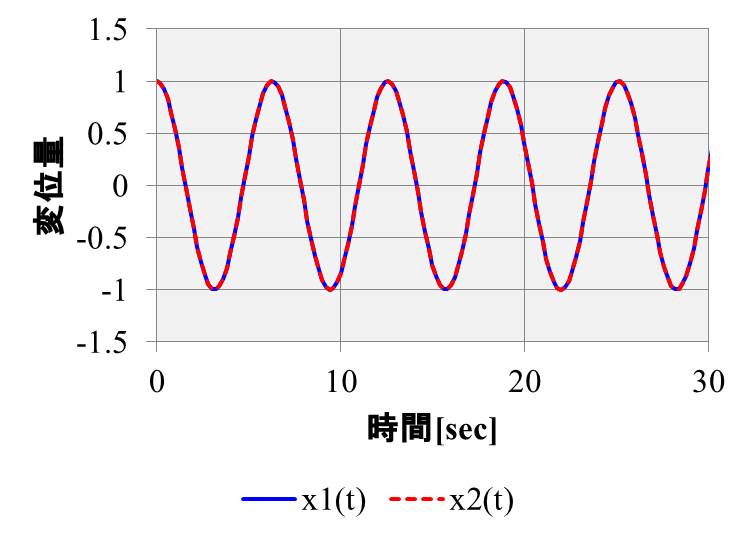
青は左側の質点の変位、赤が右側の質点の変位ですが、ぴったり一致しています。
これをアニメーションで見てみると下のようになります。
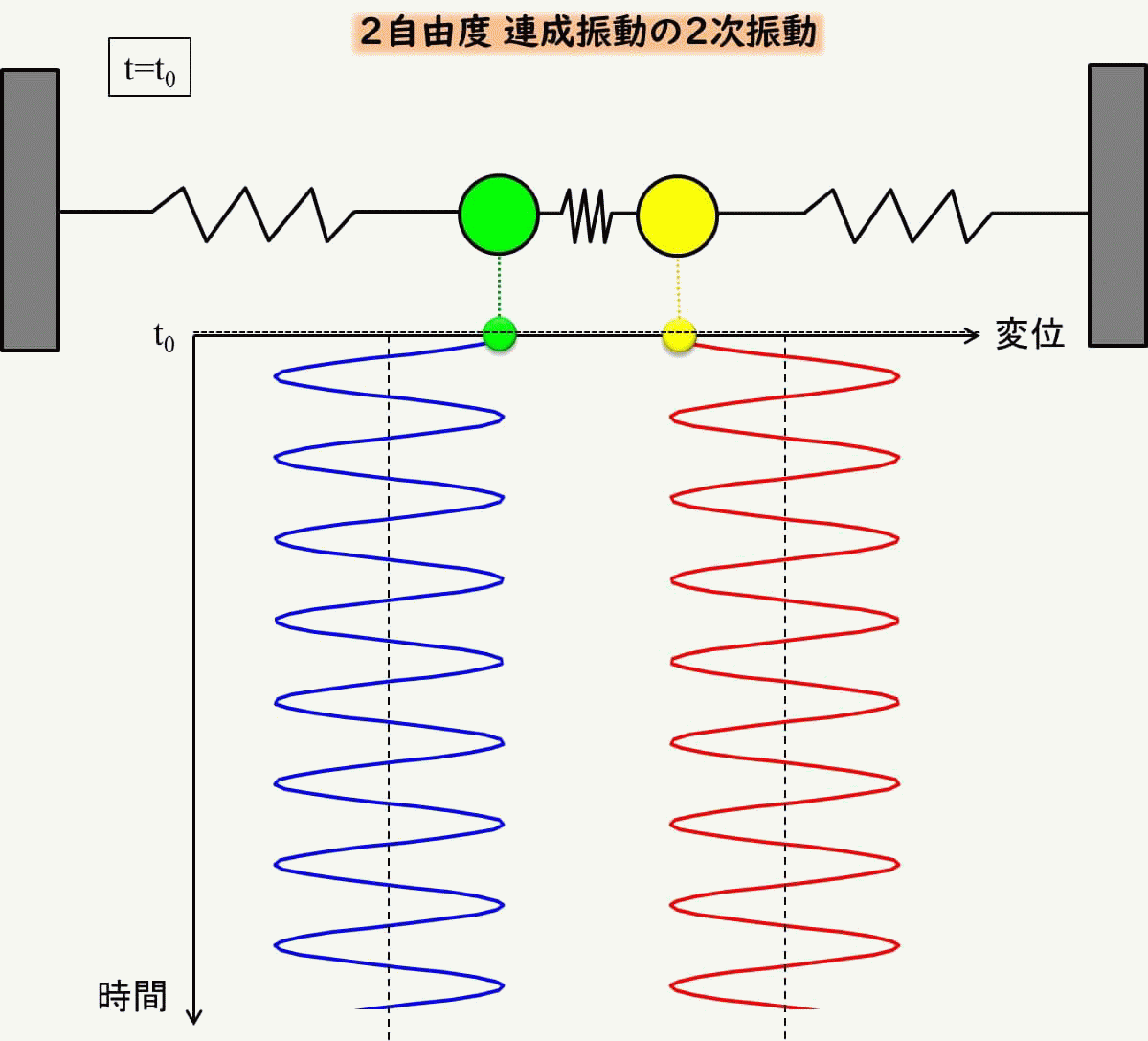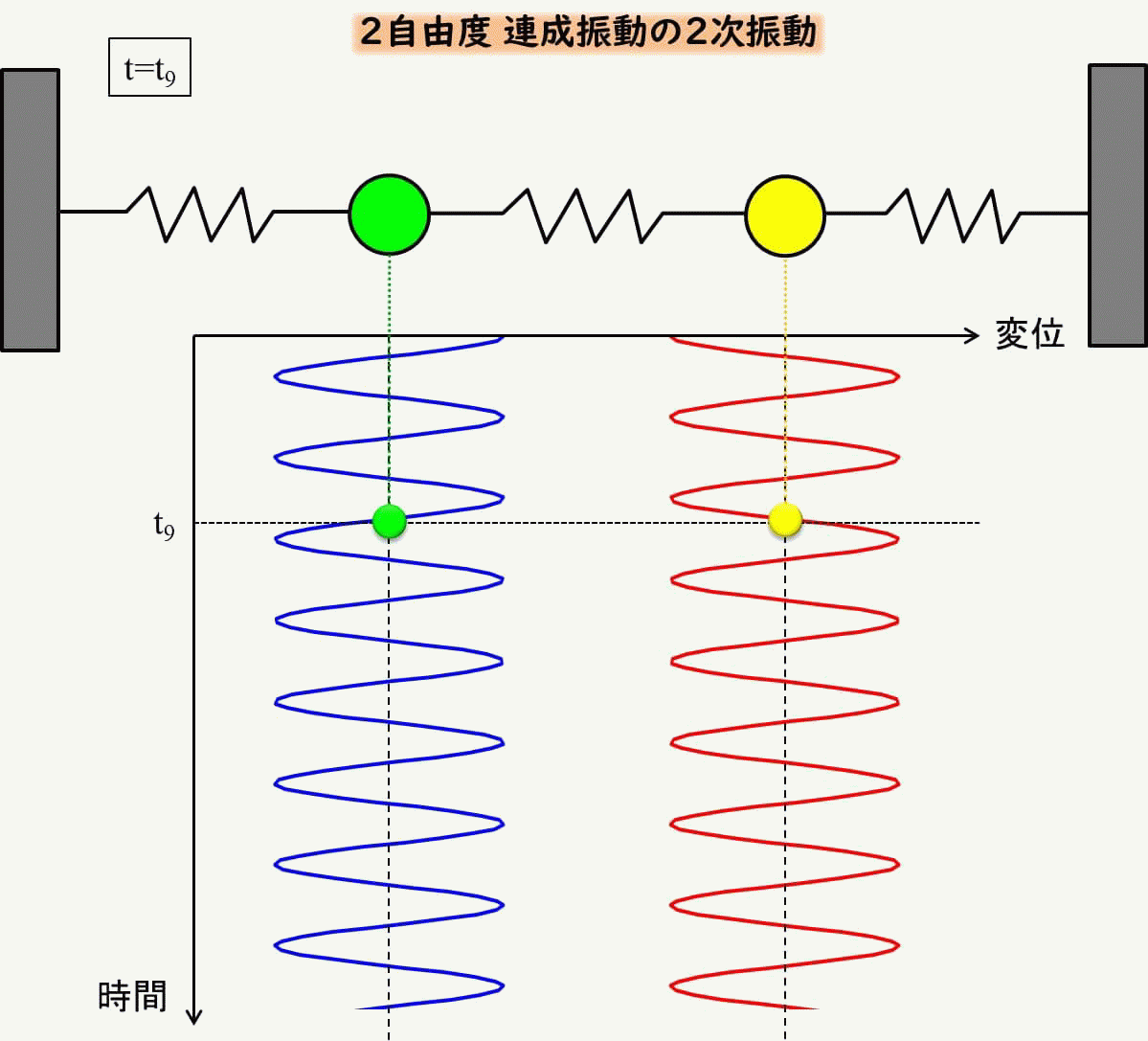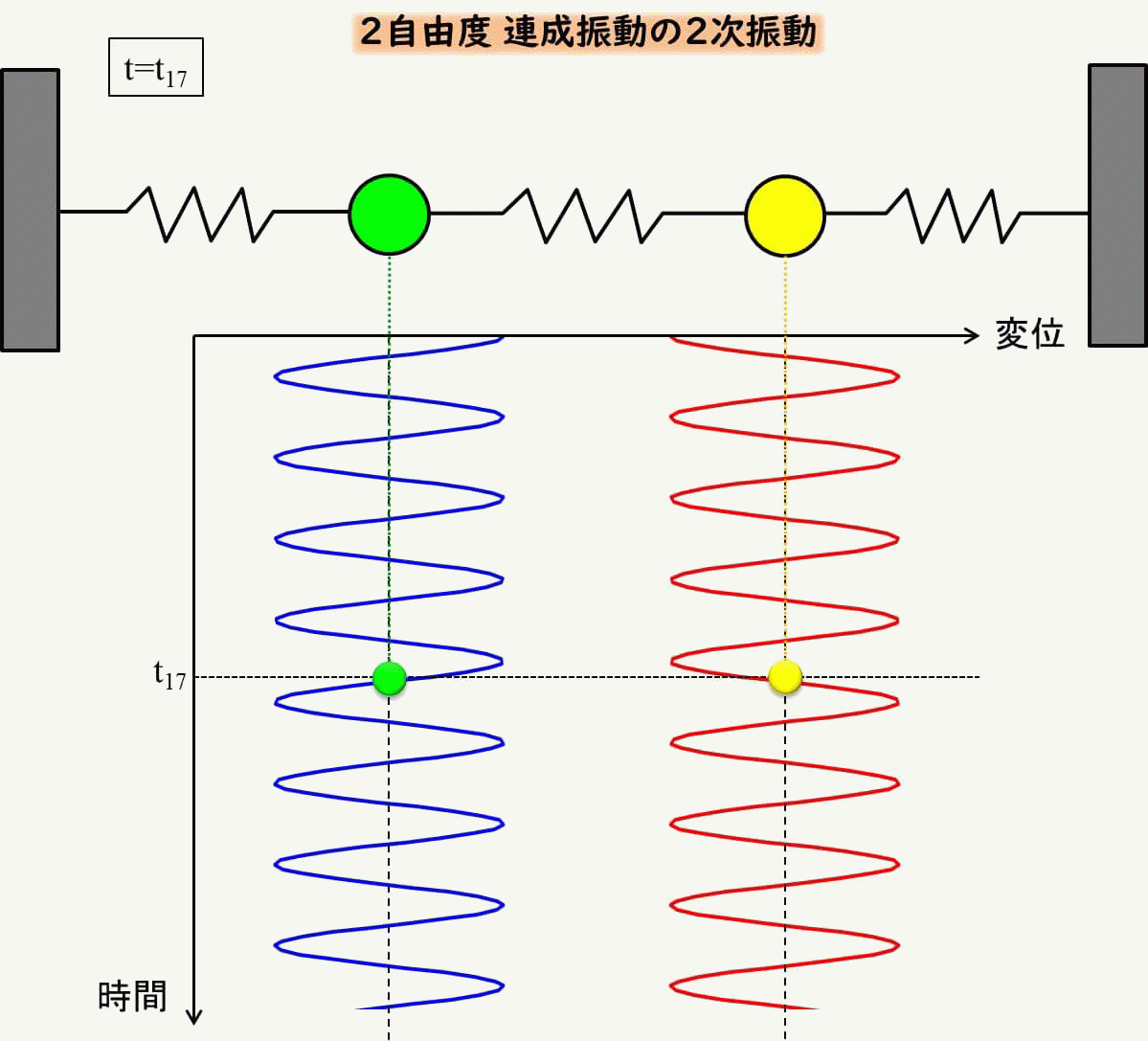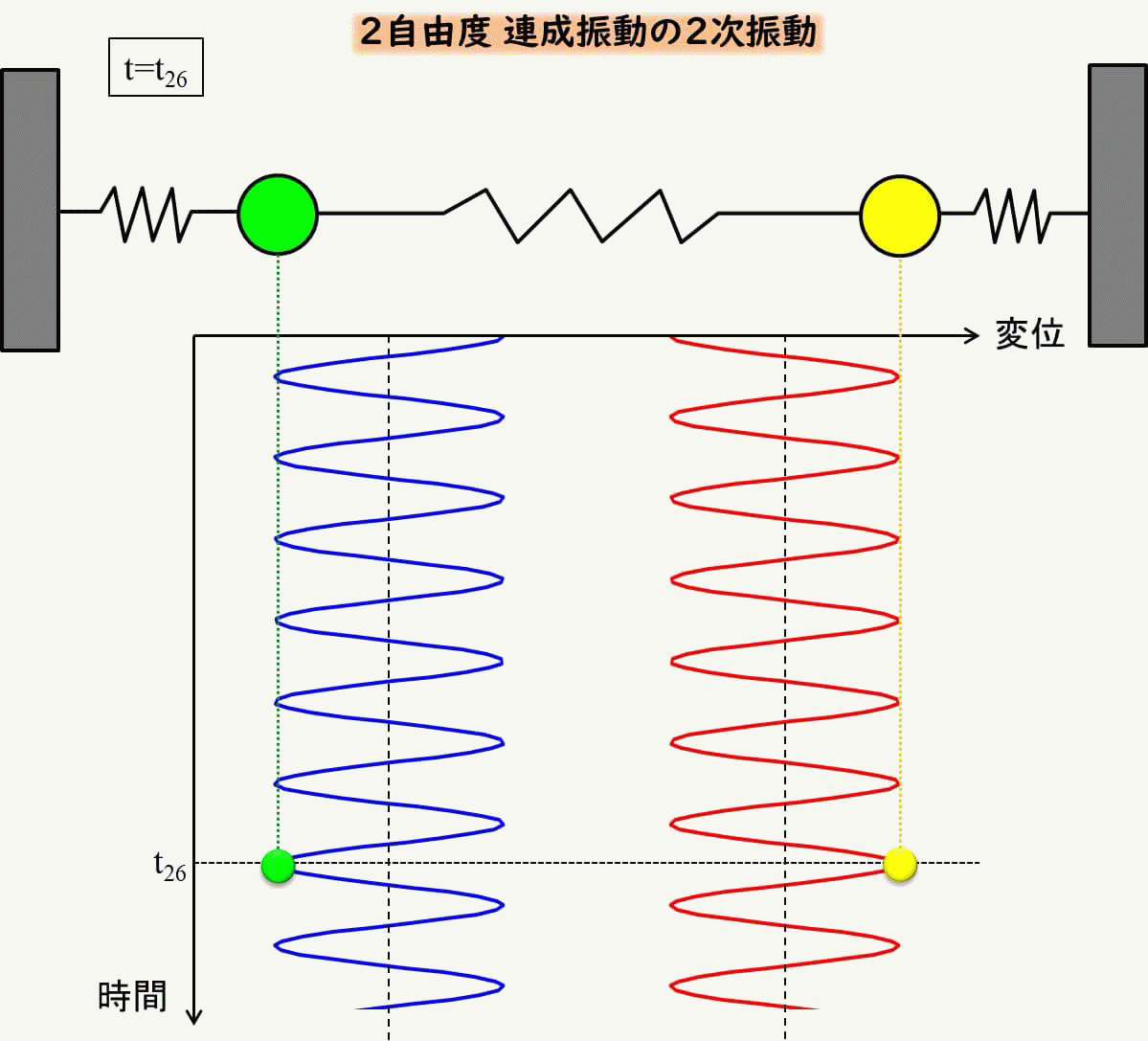
2次モードのみの初期条件
同様に2次モードのみの振動にする場合の初期条件を考えてみましょう。
$$\left(\begin{array}{c}x_1\\x_2\end{array}\right)=A\left(\begin{array}{c}1\\1\end{array}\right)cosω_0t+B\left(\begin{array}{c}1\\-1\end{array}\right)cos\sqrt{3}ω_0t+C\left(\begin{array}{c}1\\1\end{array}\right)sinω_0t+D\left(\begin{array}{c}1\\-1\end{array}\right)sin\sqrt{3}ω_0t・・・⑦$$
⑦式の1次モードに関わる成分の係数を0にするように、初期条件を決めてあげればよいわけです。
1次モードに関わる成分の係数はAとCですね。
$$A=\frac{x_{10}+x_{20}}{2}$$
$$C=\frac{v_{10}+v_{20}}{2ω_0}$$
これらが0になるように初期条件を設定します。
\(x_1、x_2\)の初期変位を\(x_{10}=1、x_{20}=-1\)、初期速度を$\(_{10}=v_{20}=0\)としましょう。
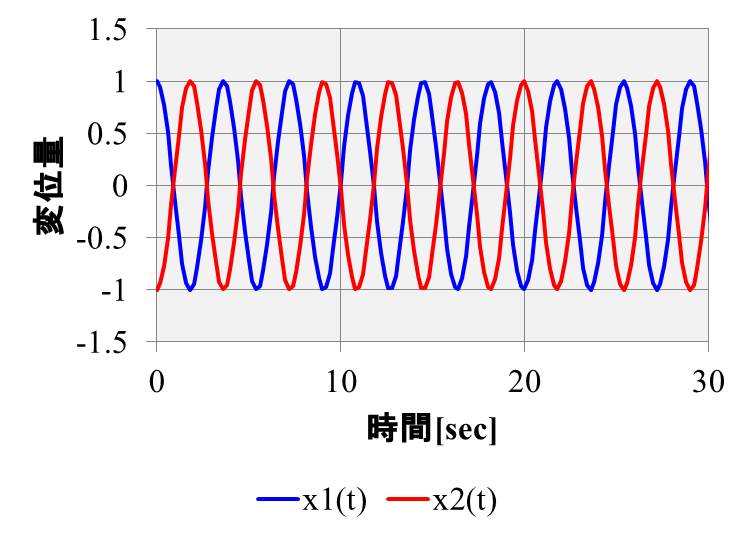
青は左側の質点の変位、赤が右側の質点の変位ですが、反対方向に常に動いていることがわかります。
これもアニメーションで見てみましょう。
まとめ
2自由度の連成振動について、最も簡単な例を紹介しました。
アニメーションを見ることで、1次、2次の固有振動についてのイメージをつけることができると思います。
このイメージをしっかり理解しておくと、自由度がさらに多くなっても理解しやすくなりますので、頭にいれておきましょう。
参考文献
- 機械力学-振動の基礎から制御まで:日高照晃、小田哲、川辺尚志、曽我部雄次、吉田和信、朝倉書店
- 第1回 ばね・質点系の連成振動から波動方程式へ 行列の固有値問題から演算子の固有値問題へ Part1 高木 周 日本機械学会誌
初心者向けの振動工学の教科書・参考書をこちらで紹介していますので、参考にしていただければと思います。
本サイトの振動工学のページはこちら。
初心者向けの教科書・参考書はこちら
振動工学の記事一覧はこちら
次の記事 → 振動・波動の基礎-⑰ 多自由度の振動の運動方程式 行列を使って表現