片持ち梁に何かモーメント荷重っていう荷重がかかっているんだけど、何これ??


荷重としてモーメントだけを作用させるケースだね。今日はモーメント荷重が片持ち梁にかかったときの曲げモーメント図について解説するね。
本日は片持ち梁にモーメント荷重が作用した時のBMD(曲げモーメント図)を解説します。
実はモーメント荷重のパターンは非常に計算が簡単ですので、サクッとやっていきましょう。
集中荷重の場合や分布荷重の場合は、過去の記事で解説していますので、そちらを是非参考にしていただければと思います。
過去記事(参考)
動画でも解説していますので、下記動画を参考にしていただければと思います。
モデル
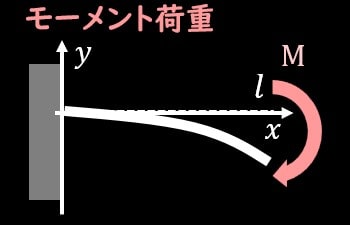
片持ち梁にモーメント荷重が作用している場合、上図のようなモデルとなります。
注意すべき点としては、集中荷重や分布荷重の場合は、荷重が作用することによって、外力によるモーメントが発生しますが、
モーメント荷重の場合、 モーメント荷重によって外力が新たに生まれて作用することはありません。
ただし、モーメント荷重による反力などは発生する可能性はありますので、ご注意ください。
※片持ち梁の場合は反力も発生しませんが、単純梁の場合などでは反力が生じます。
BMD(曲げモーメント図)を書く
曲げモーメント図を描く5ステップは過去の記事でも解説していますので、そちらも参考にしていただければと思います。
5ステップは下記のとおりでしたね。
BMDの描き方
- 座標軸をとる
- 外力のつり合いの式を立てる
- 切り出して切り出した部分のせん断力を書く
- せん断力によるモーメントを書く
- 切り出して面に注目して、せん断力によるモーメントにつり合うように、曲げモーメントを書く
片持ち梁の座標軸に関しては、2パターン考えられますが、今回は下図のように固定端を原点にとります。

ステップ2の力のつり合い、モーメントのつり合いを考えてみましょう。
つり合いの条件を考える
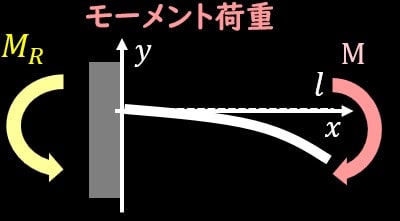
さて、梁にかかっている力を考えてみるわけですが、考えるべきは3つ、\(x\)方向、\(y\)方向、モーメントのつり合いです。
今回モーメント荷重のみが作用しているので、\(x\)方向、\(y\)方向のつり合いの式を立てることはできませんね。
モーメントのつり合いですが、モーメント荷重$M_0$と固定端に作用するモーメント\(M_R\)がつりあうことになるので、
$$M_0=M_R$$
となりますね。
せん断力を考える
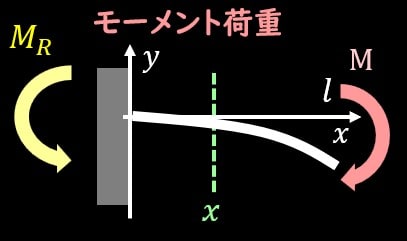
せん断力を考える場合、梁の適当な位置を切り出して、力のつり合いを考えるわけなのですが、
切り出してみると、外力、反力が一切発生していないので、せん断力はゼロとなります。
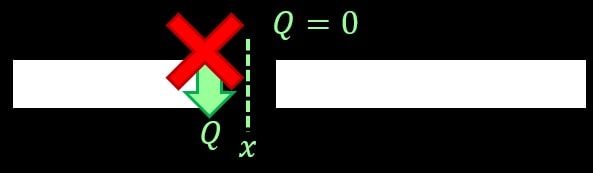
上図のようにどこを切ってもせん断力はゼロ、つまりSFD(せん断力図)は下図のようになります。

このようにせん断力が発生していない状況になるので、次のステップで考える『せん断力によるモーメント』もゼロとなります。
切り出した面のモーメントのつり合い
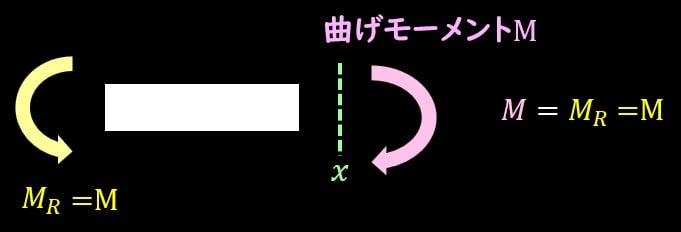
最後のステップへ参りましょう。
曲げモーメントを考えるために、梁の適当な場所を切り出し、モーメントのつり合いを考えます。
切り出すと、固定端の部分に$M_R$の反モーメントが発生しているので、このモーメントとつり合うように曲げモーメント\(M\)を発生させる必要があります。
切り出した部分のモーメントのつり合いを考えると、
$$M=-M_R=-M_0$$
となり、どの位置で梁を切っても一定となることがわかります。
曲げモーメント図を書くと下記のようになりますね。

まとめ
モーメント荷重が作用している場合のBMD(曲げモーメント図)の描き方を解説しました。
BMDの描き方
- 座標軸をとる
- 外力のつり合いの式を立てる
- 切り出して切り出した部分のせん断力を書く
- せん断力によるモーメントを書く
- 切り出して面に注目して、せん断力によるモーメントにつり合うように、曲げモーメントを書く
片持ち梁+モーメント荷重の場合のBMD(曲げモーメント図)

計算自体は非常に簡単ですので、モーメント荷重のケースは覚えるのではなく、サッと計算してしまった方が良いですね。
初心者向けの教科書・参考書もこちらで紹介しておりますので、参考にしていただければと思います。
材料力学の記事一覧はこちら。
