単純梁の等分布荷重のたわみの式って、片持ち梁のときと同じなの?


求め方は片持ち梁の時と同じだよ。曲げモーメント図さえ求まっていれば簡単に求められます。
本日は単純梁に等分布荷重がかかった場合のたわみの式を導出します。
過去の記事で、単純梁に等分布荷重をかけたときのBMD(曲げモーメント図)を求めていますので、そちらもぜひ参考にしてください。
動画でも解説していますので、是非そちらも参考にしていただければと思います。
単純梁の等分布荷重のモデル
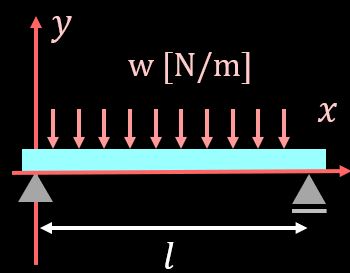
上図のように梁の両端をピン支点とローラー支点で固定した梁が単純梁です。
(教科書などによっては、両方をピン支点とすることもありますが、ここでは片側をローラー支点としています)
この単純梁に分布荷重をかけることを考えるのですが、梁全体に一様に分布荷重をかけたケースを考えます。
曲げモーメントの式
曲げモーメントの式は下記のように表すことができます。
$$M=\frac{EI}{ρ}$$
\(E\)はヤング率、\(I\)は断面2次モーメント、\(ρ\)は曲率半径を表します。
また、曲率半径\(ρ\)については、下記のようにも表すことができます。
$$ρ=\frac{dθ}{dx}=\frac{d^2y}{dx^2}$$
ここで\(θ\)はたわみ角を表します。
これらの式については過去の記事で解説していますので、参考にしていただければと思います。
さらに、曲げモーメントについては前回の記事で求めていて、下記のように表すことができます。
$$M=\frac{wx}{2}(l-x)$$
以上の式を組み合わせると下記のような微分方程式を得ることができます。
$$\frac{d^2y}{dx^2}=\frac{wx}{2EI}(l-x)$$
微分方程式を解く
上述の微分方程式の解き方ですが、下記の2ステップです。
微分方程式の解き方
- 両辺を積分する
- 積分定数を境界条件(初期条件)によって求める
これは直接積分形と呼ばれる、微分方程式の中でも簡単なタイプの微分方程式の解き方でしたね。
両辺を積分する
それでは微分方程式の両辺を積分していきましょう。
一回積分すると、
$$\frac{dy}{dx}=\frac{w}{2EI}\left(\frac{x^2l}{2}-\frac{x^3}{3}\right)+C_1$$
となります。
\(C_1\)は積分定数です。
さらにもう一度積分をすると、
$$y=\frac{w}{2EI}\left(\frac{x^3l}{6}-\frac{x^4}{12}\right)+C_1x+C_2$$
となります。
\(C_2\)は積分定数です。
境界条件を使って積分定数を求める
両辺を積分して出てきた、積分定数\(C_1,C_2\)を求めましょう。
境界条件は単純梁の場合、\(x=0\)で\(y=0\)、\(x=l\)で\(y=0\)の二つですね。
\(x=0\)の時、
$$y(0)=C_2=0$$
\(x=l\)の時、
$$y(l)=\frac{w}{2EI}\left(\frac{l^4}{6}-\frac{l^4}{12} \right)+C_1l$$
式を整理して\(C_1\)を求めると、
$$C_1=-\frac{wl^3}{12EI}$$
と求めることができます。
よって、
$$y(x)=\frac{w}{2EI}\left(\frac{x^3l}{6}-\frac{x^4}{12}\right)-\frac{wl^3}{12EI}x$$
となります。
さて、最大たわみ量がどのようになるかですが、今回の等分布荷重は梁の中心から対称になっているので、
梁の長さの半分の位置で最大たわみが生じますね。
$$y(\frac{l}{2})=\frac{-5wl^4}{384EI}$$
となります。
まとめ
以上、等分布荷重のたわみの式を導出しました。
単純梁の等分布荷重のたわみの式
$$y(\frac{l}{2})=\frac{-5wl^4}{384EI}$$
たわみの式の導出の仕方
- 曲げモーメント図(BMD)を求める
- 曲げモーメントの式を積分し、境界条件から積分定数を求める
曲げモーメントの式
$$M=\frac{EI}{ρ}$$
たわみの式の導出は片持ち梁の場合と同じですので、流れをしっかりと理解しておきましょう。
初心者向けの教科書・参考書もこちらで紹介しておりますので、参考にしていただければと思います。
材料力学の記事一覧はこちら。
