単純梁にも分布荷重がかかっているんだけど、これも片持ち梁と同じ解き方なの?


そうだよ。曲げモーメントを考える際に、積分をすることで求めることができるので解説するね。
本日は単純梁の等分布荷重の曲げモーメント図の書き方を解説します。
基本的には片持ち梁の場合と求め方は同じなので、是非、過去の記事も参考にしてくださいね。
下記の動画でも解説していますので、そちらも是非参考にしていただければと思います。
モデル
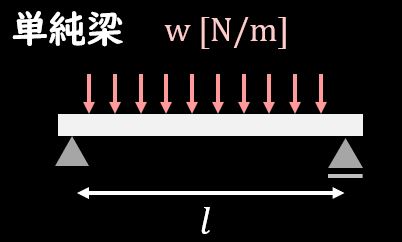
上図のように単純梁に等分布荷重\(w\)がかかっている状態を考えてみましょう。
梁の長さを\(l\)、\(w[N/mm]\)の分布荷重が単位長さあたりにかかっているとします。
BMDの書き方のおさらい
BMD(曲げモーメント図)の書き方は過去の記事で解説していますので、そちらもぜひ参考にしていただければと思います。
BMDは下記の5ステップで描くことができます。
BMDの描き方
- 座標軸をとる
- 外力のつり合いの式を立てる
- 切り出して切り出した部分のせん断力を書く
- せん断力によるモーメントを書く
- 切り出して面に注目して、せん断力によるモーメントにつり合うように、曲げモーメントを書く
座標軸の取り方については、今回は下図のようにとって考えますので、2つ目のつり合いの式を考えるところからスタートしましょう。
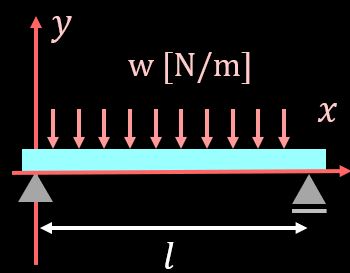
つり合いの条件を考える
単純梁の力のつり合いを考える際、両端の支点からの反力を考える必要があります。
まずトータルの荷重は、分布荷重が\(w\)で梁の長さが\(l\)なので、\(wl\)と書くことができます。
この荷重とつりあうように反力が発生しますので、
$$wl=R_a+R_b$$
と書くことができます。
反力は下図のように設定しております。
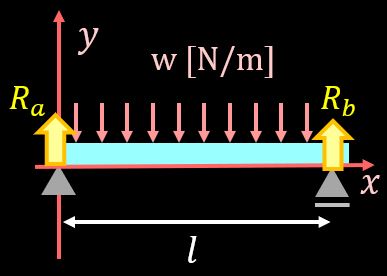
次にモーメントのつり合いですが、左側の支点から考えると、
$$\int^l_0 w×xdx-R_bl=0$$
このように積分して外力によるモーメントを表すことができます。
積分計算すると、
$$\frac{1}{2}wl^2-R_bl=0$$
と表すことができ、
$$R_b=\frac{1}{2}wl$$
と反力\(R_b\)を求めることができます。
力のつり合いの式に代入すると、もう片方の反力\(R_a\)は
$$R_a=\frac{1}{2}wl$$
と求めることができます。
切り出してせん断力を求める
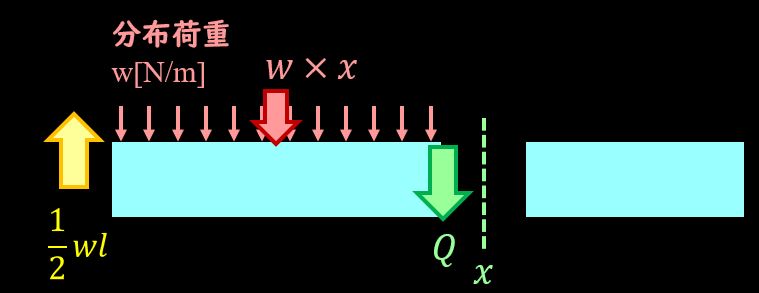
次のステップとして、梁の途中を切り出して、せん断応力を考えてみましょう。
上図のように、梁の途中で切断します。
この切り出した状態でも力のつり合いやモーメントのつり合いが成立しなければいけませんので、
まずは力のつりあいについて考えてみましょう。
切り出した座標位置は\(x\)なので、分布荷重から受ける力は\(w×x\)となりますね。
また、固定端には上向きに\(\frac{1}{2}w×l\)の力が反力として発生していますので、分布荷重と比較すると、梁中央で符号が反転しますね。
このままだと、力のつり合いが保たれない、ということで、切断面に下向きの力をかけて、つり合いを保つようにします。
下向きの力を正とすると、せん断力Qは
$$Q=\frac{1}{2}wl-wx=\frac{w}{2}(l-2x)$$
となります。
せん断力図を書くと下記のようになりますね。
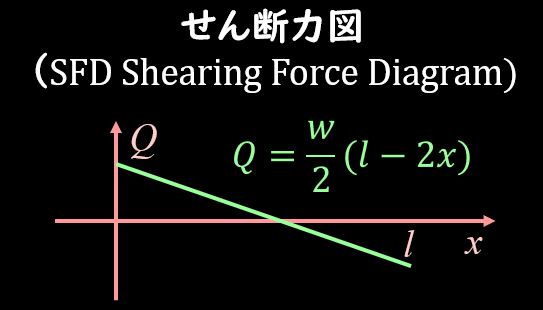
せん断力によるモーメントを書く
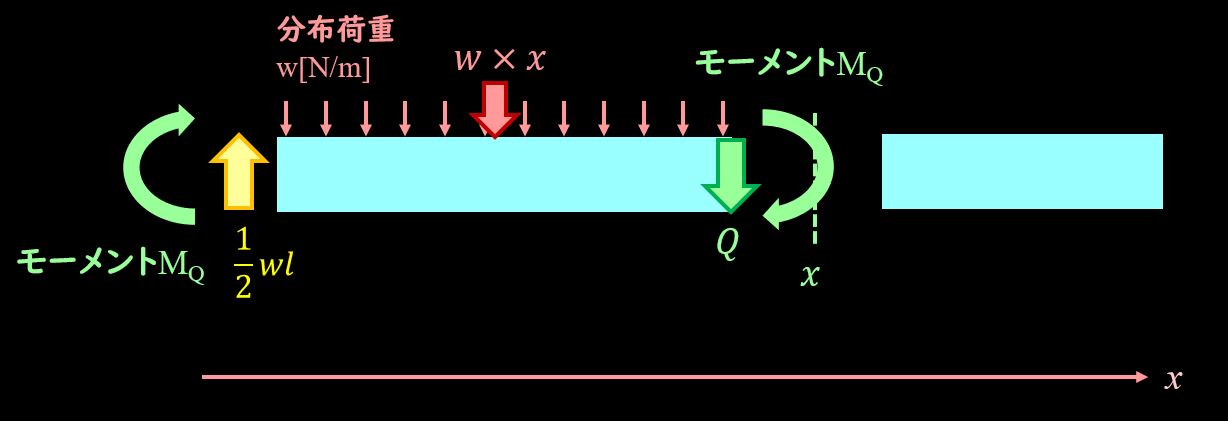
せん断力が切断面に発生していますので、せん断力によるモーメントを書きましょう。
切断面の座標がxでせん断力がQなので、せん断力によるモーメントを$M_Q$とすると、
$$M_Q=Q×x=\frac{w}{2}x(l-2x)$$
となります。
切断した部分でのモーメントのつり合い
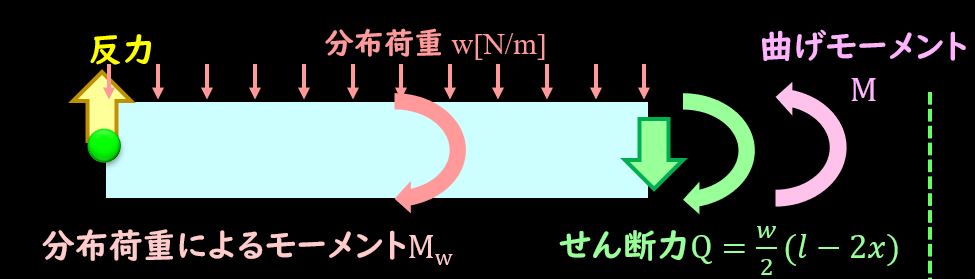
それでは最後のステップとして、切断部分でのモーメントのつり合いを考えていきましょう。
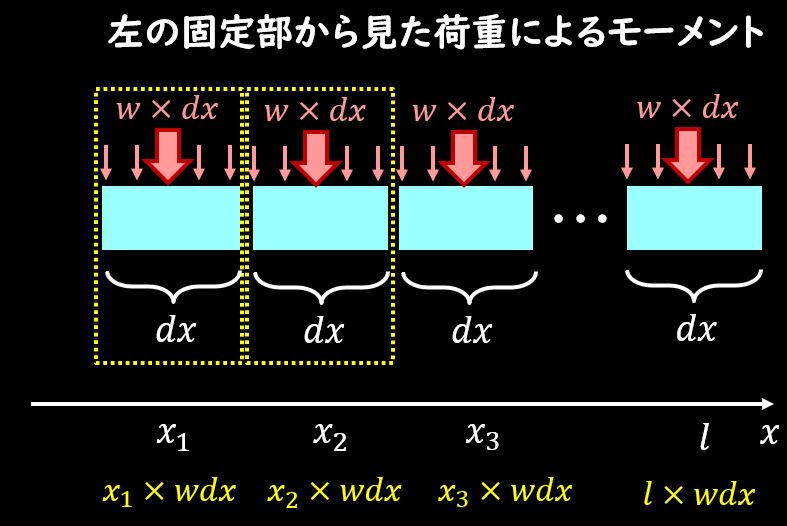
まずは切り出した部分で、とあるX座標を考え、分布荷重によるモーメントがどのようになるかを考えましょう。
力のつり合いを考えた場合と同じように、ここでも積分を使って考える必要があります。
梁内の微小領域\(dX\)を考えると、微小領域内での力は、
$$w×dX$$
と書くことができますので、この微小領域でのモーメントは
$$X×wdX$$
と書き表すことができます。
これを\(0〜x\)まで積分してあげると、分布荷重によるモーメントを求めることができて、
$$\int^x_0XwdX=\frac{w}{2}x^2$$
と表すことができます。
これで切り出した部分にかかっているモーメントは全て書き表すことができていて、せん断力によるモーメントと外力によるモーメントの2つですね。
これらがつりあうように曲げモーメント\(M\)を切断面に発生させる必要がありますので、モーメントのつり合いから
$$M=\frac{w}{2}x^2+\frac{w}{2}x(l-2x)$$
式を整理すると
$$M=\frac{w}{2}x(l-x)$$
このように曲げモーメントがもとまり、曲げモーメント図を描くと、下図のようになります。
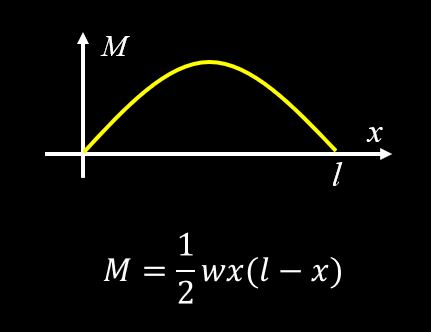
以上で単純梁に等分布荷重がかかったときのBMD(曲げモーメント図)を描くことができました。
まとめ
単純梁の等分布荷重がかかった場合の曲げモーメント図を求めました。
単純梁 等分布荷重のBMD


BMDの描き方
- 座標軸をとる
- 外力のつり合いの式を立てる
- 切り出して切り出した部分のせん断力を書く
- せん断力によるモーメントを書く
- 切り出して面に注目して、せん断力によるモーメントにつり合うように、曲げモーメントを書く
片持ち梁の時と同じように積分計算が出てきて、苦手な方は理解するのに苦労するかもしれませんが、
ここの積分計算は非常に大切な考え方ですので、自分の手を動かしながら、しっかりとマスターしていただければと思います。
初心者向けの教科書・参考書はこちら
材料力学の記事一覧はこちら
次の記事 → 材料力学 構造力学 単純梁の等分布荷重 たわみの式を導出
