等分布荷重のBMDはわかったんだけど、たわみはどうやって求めるの?


BMDからたわみを求めるのは集中荷重や単純梁のときと同じだよ。今日は片持ち梁の等分布荷重のたわみの式を導出してみよう。
今回は片持ち梁の等分布荷重のたわみの式を導出してみましょう。
BMD(曲げモーメント図)については過去の記事で解説していますので、そちらを参考にしていただければと思います。
また、動画でも解説しておりますので、そちらも是非ご覧ください。
片持ち梁 等分布荷重のモデル
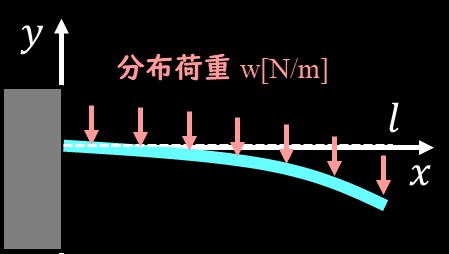
上図のように、梁の片側を完全固定している梁を片持ち梁と呼んでいます。
その片持ち梁に等分布荷重が梁全体にかかっている場合を考えていきましょう。
ちなみに、等分布荷重をかけるというのは、均一の大きさで梁全体に荷重をかけている状態のことを指します。
曲げモーメントの式
曲げモーメントの式は下記のように表すことができます。
$$M=\frac{EI}{ρ}$$
\(M\)は曲げモーメント、\(E\)はヤング率、\(I\)は断面2次モーメント、\(ρ\)は曲率半径です。
これらの解説については過去の記事を参考にしていただければと思います。
また、曲率半径\(ρ\)の逆数は下記のように表すことができます。
$$\frac{1}{ρ}=\frac{d^2y}{dx^2}$$
これらの解説については、過去の記事で解説していますので参考にしていただければと思います。
片持ち梁の等分布荷重のBMDは前回の記事より、下記のように表すことができます。
$$M=-\frac{w}{2}(l-x)^2$$
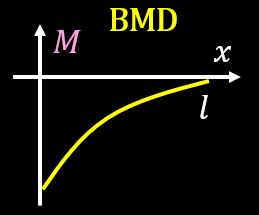
この式を曲げモーメントの式に代入すると下記のようになります。
$$\frac{d^2y}{dx^2}=-\frac{w}{2EI}(l-x)^2$$
この微分方程式を解くことによって、たわみの式を導出することになります。
微分方程式を解く
さて、上述のたわみについての微分方程式ですが、解き方は下記の2ステップとなります。
微分方程式の解き方
- 両辺を積分する
- 積分定数を境界条件(初期条件)によって求める
いわゆる直接積分形と呼ばれる微分方程式を解くことになります。
両辺を積分する
それでは積分をしていきましょう。
まず両辺を1回積分すると、
$$\frac{dy}{dx}=\int\frac{-w}{2EI}(l-x)^2dx$$
かっこの2乗を計算しておきましょう。$$\frac{dy}{dx}=\int\frac{w}{2EI}(l^2-2lx+x^2)dx$$
積分すると、
$$\frac{dy}{dx}=\frac{w}{2EI}(\frac{1}{3}x^3-lx^2+l^2x)+C_1$$
\(C_1\)は積分定数です。
それではもう一度両辺を積分してみましょう。
$$y=\int\left(\frac{w}{6EI}(\frac{1}{3}x^3-lx^2+l^2x)+C_1\right)dx$$
積分を実行すると、
$$y=\frac{-w}{2EI}(\frac{1}{12}x^4-\frac{l}{3}x^3+\frac{l^2}{2}x^2)+C_1x+C_2$$
\(C_2\)は積分定数です。
このように積分定数が2つ(\(C_1,C_2\))が出てくるので、これらを求めるのが次のステップとなります。
境界条件から積分定数を求める
それでは次のステップとして、積分定数を境界条件を使って求めましょう。
片持ち梁の場合の境界条件は下記の2つとなります。
・\(x=0で\frac{dy}{dx}=0\)
・\(x=0\)で\(y=0\)
これらは固定端ではたわみ角ゼロ、変位量がゼロという意味ですね。
これらの条件を使って積分定数を求めます。
まず、\(x=0\)で\(\frac{dy}{dx}=0\)より、
$$\frac{dy}{dx}=C_1=0$$
次に\(x=0\)で\(y=0\)より、$$y(0)=C_2=0$$
と、積分定数はともにゼロとなります。よって、
$$\frac{dy}{dx}=\frac{w}{2EI}(\frac{1}{3}x^3-lx^2+l^2x)$$$$y=\frac{-w}{2EI}(\frac{1}{12}x^4-\frac{l}{3}x^3+\frac{l^2}{2}x^2)$$
となります。最大たわみ量を計算
片持ち梁の場合、\(x=l\)の部分、すなわち、梁の先端で最大たわみ量となりますので、yの式に\(x=l\)を代入しましょう。$$y(l)=\frac{-w}{2EI}(\frac{1}{12}l^4-\frac{l}{3}l^3+\frac{l^2}{2}l^2)=-\frac{wl^4}{8EI}$$
このように最大たわみ量を求めることができます。まとめ
以上、片持ち梁の等分布荷重の最大たわみ量、たわみの式を導出しました。片持ち梁の等分布荷重のたわみの式
$$y(l)=-\frac{wl^4}{8EI}$$
たわみの式の導出の仕方
- 曲げモーメント図(BMD)を求める
- 曲げモーメントの式を積分し、境界条件から積分定数を求める
曲げモーメントの式
$$M=\frac{EI}{ρ}$$
導出過程はBMD(曲げモーメント図)さえわかっていれば集中荷重の場合と全く同じ手順で求めることができます。前回の記事の通り、曲げモーメント図の導出が等分布荷重の場合、集中荷重と異なりますので、是非そちらも理解しておくことをおすすめします。
初心者向けの教科書・参考書はこちら
材料力学の記事一覧はこちら
次の記事 → 材料力学・構造力学 単純梁の等分布荷重の曲げモーメント図
https://youtu.be/vJv9wzDQ_w0
