曲げモーメント図って何??書き方がよくわからないよ


曲げモーメントについては材料力学でもつまづきやすい所だから、丁寧に説明するね。
本日は曲げモーメント図(BMD)の書き方を解説します。この曲げモーメント図は梁のたわみの計算であったり、曲げによって壊れやすい部分を特定するために必要で、非常に重要な役割を担っています。
一方で苦手な方が多い部分でもありますので、しっかりと解説していきます。曲げについては過去の記事でも解説していますので、参考にしていただければと思います。
参考記事
下記の動画でも解説していますので是非ご覧ください。
曲げモーメント図とは
曲げモーメント図は、梁を曲げた時に、曲げモーメントが各場所でどのような大きさになっているかを示したものです。
片持ち梁の場合、下図のような図になります。
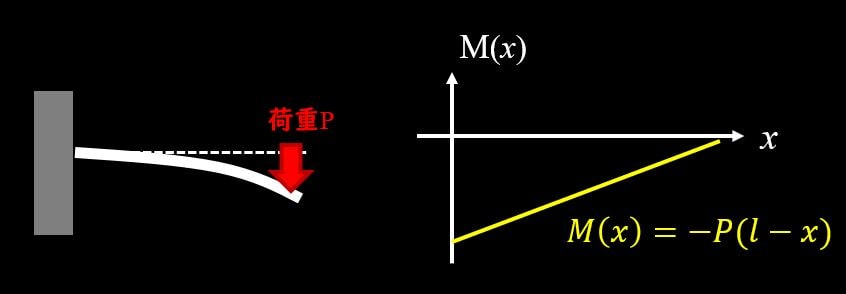
曲げモーメント図が重要な理由
曲げモーメント図が重要な理由
- 1番大きな曲げモーメントがかかる場所がわかる
- 梁のたわみ形状がわかる
- たわみの式を求められるようになる
これら3つが主な理由です。
材料力学は部材が壊れないようにするためにはどうしたらよいか、がわかるようになる学問です。
曲げ変形させたときに、部材のどこが1番壊れやすいかは、曲げモーメントが最大となる部分になります。
片持ち梁では曲げモーメントは付け根の部分で最大になるので、付け根から壊れることになりますね。
このように曲げ変形に対して、どこが壊れやすいかを判断するために、曲げモーメント図は重要になってくるわけです。
さらに、曲げモーメントがどのようになっているかを知ることで、梁がどのようにたわむか、ということがわかります。
壊れないのは当然として、できるだけたわみを少なくするためにはどうすればいいか、という議論は結構重要です。
橋とかでも、人が歩いただけでめっちゃたわんでしまうとものすごく怖いことになってしまいます。
この曲げモーメント図からたわみへの繋ぎ方は別途解説しますので、そちらを参考にしていただければと思います。
曲げモーメント図、大事であることがわかってきましたでしょうか?s
それでは曲げモーメント図の書き方について解説していきます。
曲げモーメント図(BMD)の書き方
BMDの描き方
- 座標軸をとる
- 外力のつり合いの式を立てる
- 切り出して切り出した部分のせん断力を書く
- せん断力によるモーメントを書く
- 切り出して面に注目して、せん断力によるモーメントにつり合うように、曲げモーメントを書く
以上、5ステップです。
それぞれに少し注意事項もありますので、詳しく説明していきますね。
座標軸をとる
今回は片持ち梁の例を見てみましょう。
梁の端に荷重Pが下向きにかかっている状態です。
まずはこの片持ち梁について座標軸をとります。
ここで、座標軸をとるとしたときに、下図のどちらがよいでしょう?
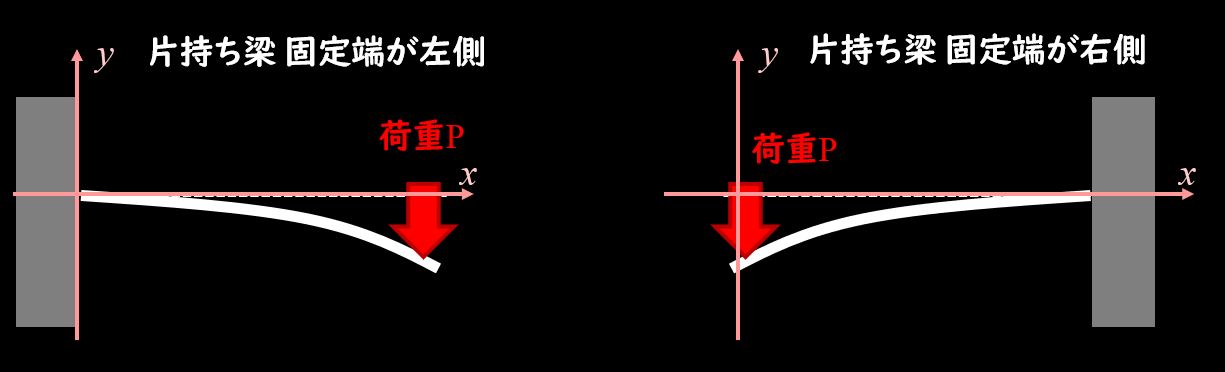
これの正解はどっちでもOK、というのが答えです。
計算を簡単なのは荷重\(P\)がかかっている点を原点にとる方なので、こっちを原点にとるんだ!って説明される方もいらっしゃいますが、
どちらを選んでも答えに辿り着きますので、お好きな方を選んでください。
今回はあえて根本を原点にとって考えてみましょう。
外力のつり合いを考える
今回の場合、外力は荷重\(P\)ですね。
この荷重\(P\)によって、梁は曲がるわけですが、荷重だけが梁にかかっていると、梁は下方向へ飛んでいってしまいます。
飛んでいかないということは、力がつりあうように、他の力が梁にかかっている、ということになります。
その力というのが反力なわけですね。
反力は支点から受ける力を表し、支点による支持方法によって、発生できる反力に違いができるのでした。
それが下の表です。

今回、片持ち梁の場合ですと、固定方法は完全固定となりますので、
反力として、水平方向、鉛直方向、モーメントの3種類を発生させることができますね。
荷重Pは鉛直方向にかかる力なので、その力につりあう反力を壁から受けることになります。
さらに、剛体のつり合い条件として、力だけでなく、モーメントのつり合いも考えなければなりません。
荷重\(P\)によるモーメントは支点から先端までの距離をlとすると、\(P×l\)となり、
このモーメントにつりあうようなモーメントが支点に発生することになります。

切り出してせん断力を書き出す
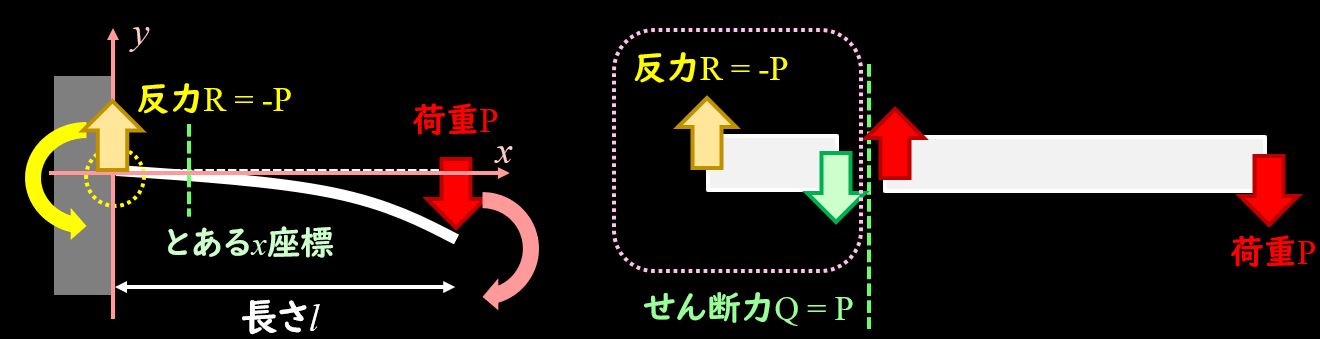
図のように片持ち梁の途中部分で切り出します。
ここでポイントとなるのは、切り出した部分も力・モーメントがつりあっている、という点です。
左側の部分をみてみましょう。
固定端の部分から反力を受けていますね。
この反力だけ切り出した部分にかかっているとすると、力のつり合いが保てていないことになります。
ここで、力がつりあわないといけないので、切り出した面に力がつりあうように、反対の向きに力\(Q\)がかかっているようにします。
この力\(Q\)と反力がつりあっているので、\(Q\)の大きさは\(P\)となります。
このように見ると、切り出した部分にせん断力が発生しているように見えますね。
このせん断力、片持ちはりの場合、どこを切っても同じ大きさとなりますので、せん断力図を書くと下図のように書けます。
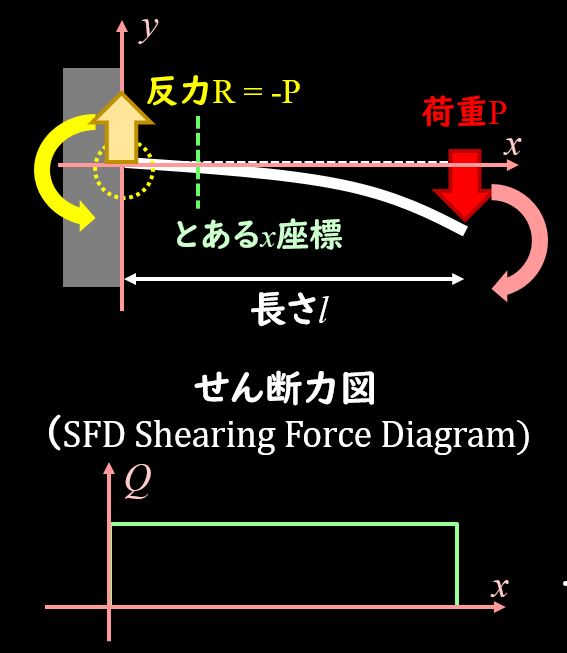
せん断力によるモーメントを書く
さて、切り出した部分をみてみると、せん断力が発生していることがわかりました。
このせん断力をみてみると、下図のようなモーメントが発生することがわかるでしょうか?
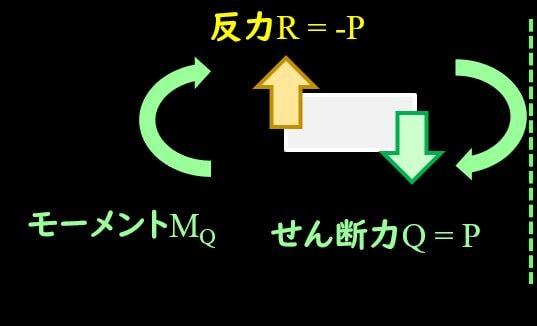
このモーメントだけだと、切り出した部分は回転してしまうので、つりあうようなモーメントを考える必要があります。
それは次のステップでの説明とさせていただきますね。
曲げモーメントを書く
さらには支点部分には反モーメントが発生していましたね?
これらを整理してみましょう。
せん断力によるモーメントは、
$$M_1=Q×x=P×x$$
固定端のモーメントは
$$M_R=P×l$$
この二つを見比べてみると、明らかに固定端のモーメントが大きく、つり合っていないことがわかります。(\(l>x\))
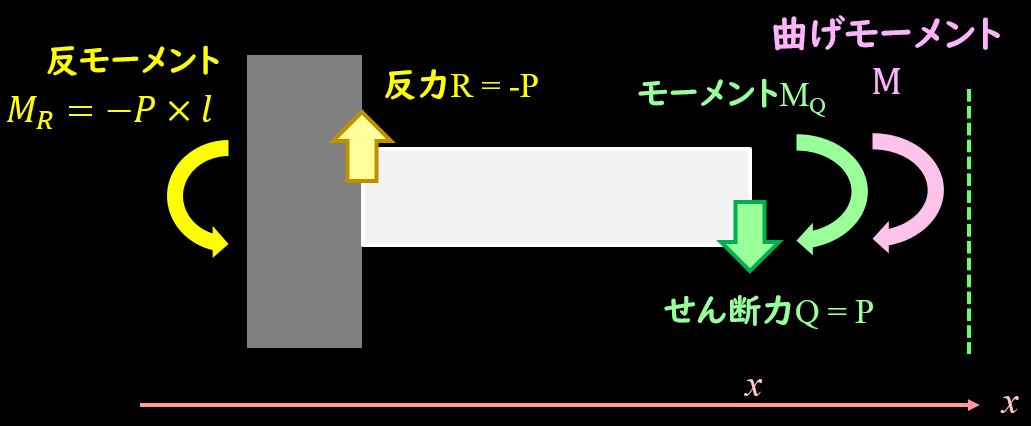
しかし、切り出した部分もモーメントがつりあっていないといけないので、切断面にモーメントを追加してあげる必要があります。
切断面にかかるモーメントがまさに曲げモーメントで、この曲げモーメント\(M\)は
$$M=-M_R+M_1=-P(l-x)$$
このように曲げモーメントをxの関数で表すことができます。
図で書いたものがBMDで、それが下記となります。
曲げモーメントの符号について
BMDを書くときに曲げモーメントについて、どちらがプラスかというのが慣例的に決まっています。

上図のような形で、下に凸に曲がる方向がプラス、上に凸に曲がる方向がマイナスです。
材料力学は部材が壊れないようにしたい学問です。
悲観的に、ネガティブに考えて安全をみて設計できるようになるのが材料力学です。
なので下向きに曲がる方向がプラスです。ネガティブなのです。
材料力学の専門家に怒られそうですね…
せん断力の符号について
こちらもSFDを書く際に、せん断力の符号も注意しなければなりません。
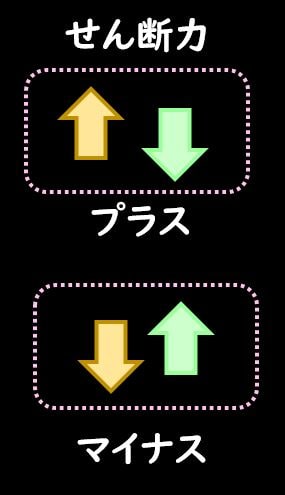
上図のような形で右側が下向きの方がプラス、右側が上むきがマイナスです。
みなさん、右肩上がりが好きですよね。
でも材料力学はネガティブなのです。
右肩下がりが好きです。
だから右肩下がりのせん断力がプラスです。
以上、完全にこじつけの覚え方です。
まとめ
本日は片持ち梁 集中荷重のBMDの書き方を解説しました。
片持ち梁の曲げモーメント図

下記の5ステップしっかりと抑えておけば、基本はOKです。
BMDの描き方
- 座標軸をとる
- 外力のつり合いの式を立てる
- 切り出して切り出した部分のせん断力を書く
- せん断力によるモーメントを書く
- 切り出して面に注目して、せん断力によるモーメントにつり合うように、曲げモーメントを書く
今後、色んな梁のBMDやSFDの書き方について解説しますので、楽しみにしていただければと思います。
初心者向けの教科書・参考書はこちら
材料力学の記事一覧はこちら
次の記事 → 材料力学 これで脱暗記!梁のたわみの式を導出する-片持ち梁編
