縦振動と横振動っていう言葉が出てきたんだけど、何が違うの?


棒とか梁とかの振動する方向によって縦振動とか横振動って使い分けるよ。今回は縦振動について解説するね。
今回は棒の縦振動について解説します。
最終的には両端固定の弦の振動とよく似た形になりますので、運動方程式がどのような形になるかをしっかりと理解しましょう。
両端固定の弦については過去の記事で解説していますので、参考にしてください。
過去記事
動画でも解説していますので、解説していますので下記も参考にしていただければと思います。
縦振動と横振動
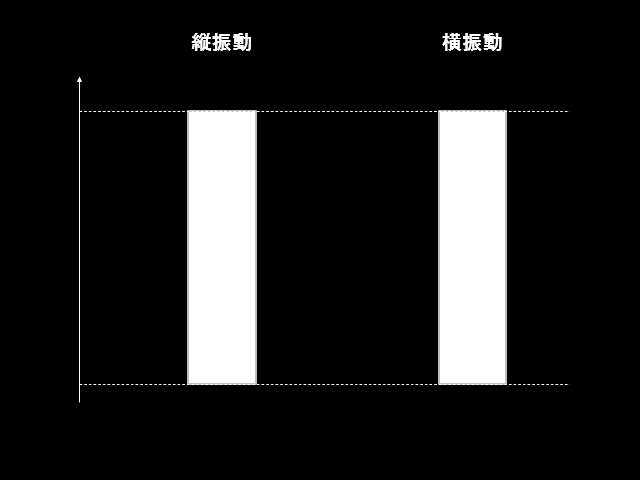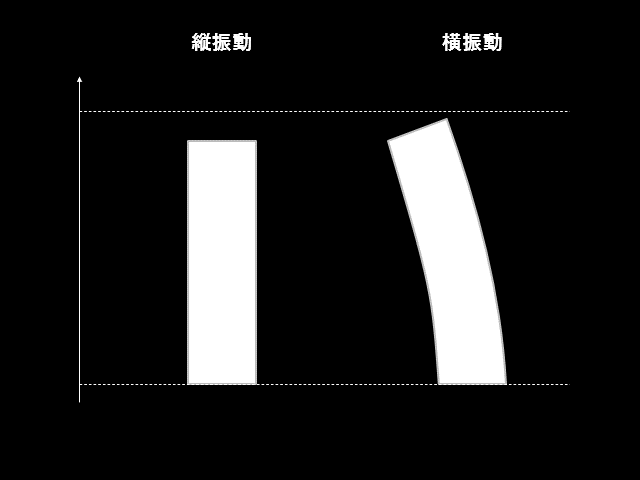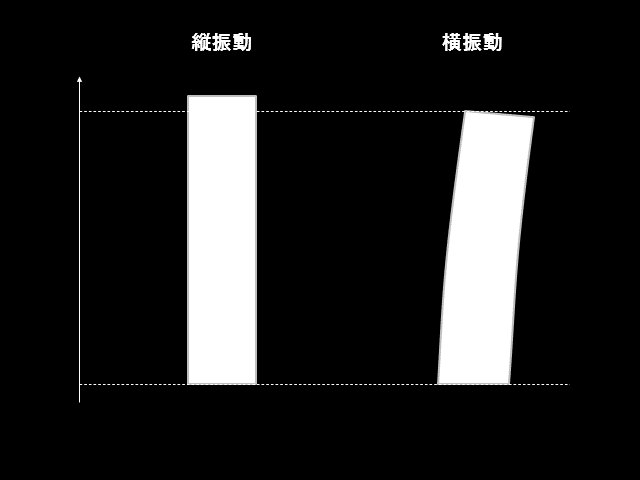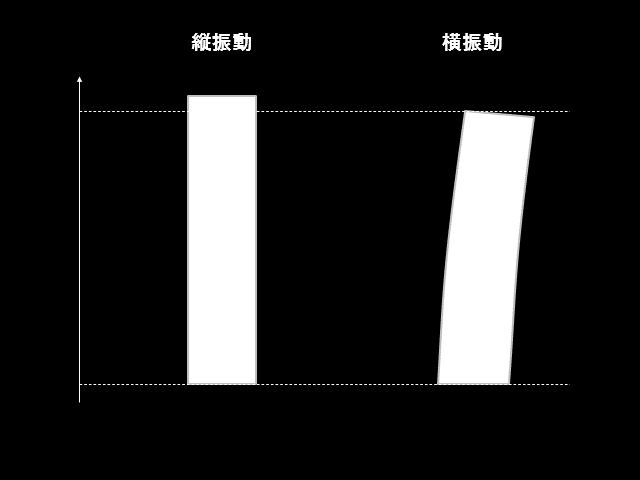
棒や梁の縦振動と横振動は上図のような振動状態を指します。
長手方向に振動する場合を縦振動、長手方向と垂直な方向に振動する場合を横振動と呼びます。

梁の長手方向が基準になるんだね。
モデル
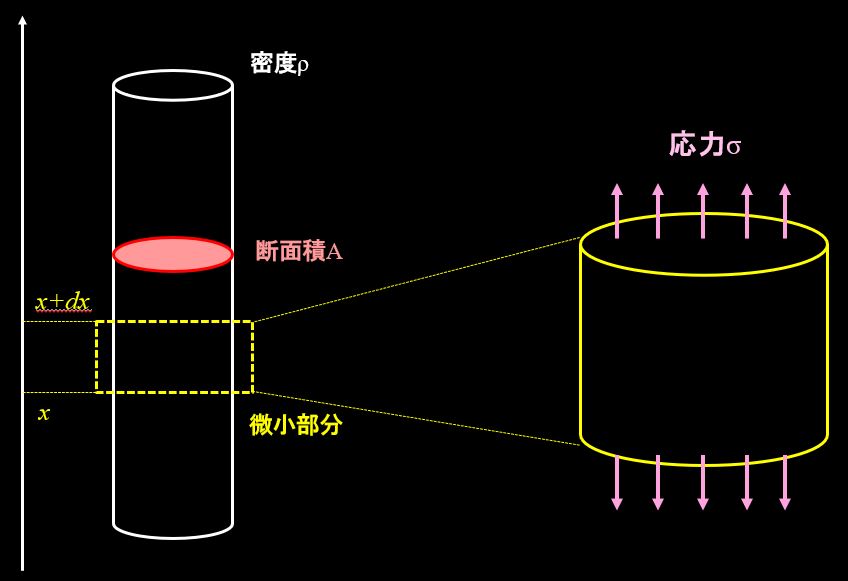
上図のように、密度が\(ρ\)の縦長の棒を用意し、棒の中の微小部分を取り出します。
棒の断面積\(A(x)\)、棒の下端を\(x\)、棒の上端を\(x+dx\)とし、振動することによって断面部分に発生する応力を\(σ\)とします。
この微小部分に応力\(σ\)が発生したときの、棒の変位を\(u\)とすると、下図のように書けます。
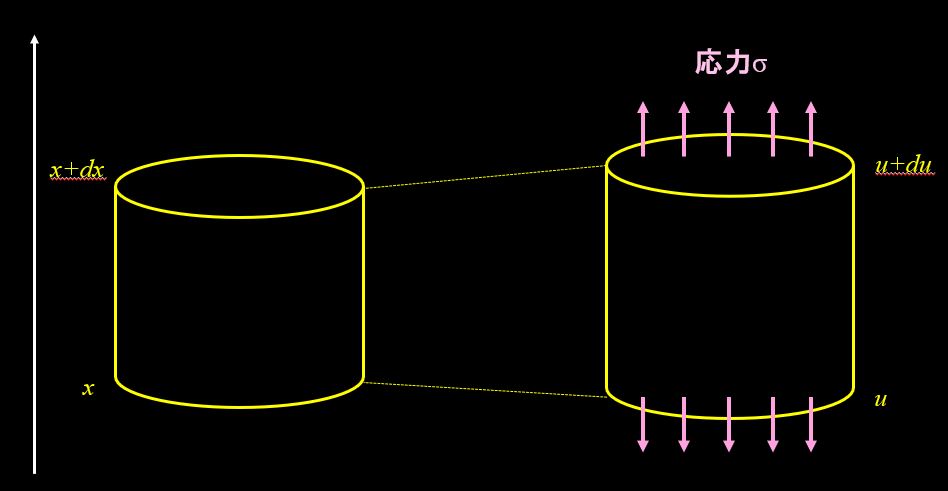
ここで、フックの法則から、 $$σ=Eε=E\frac{\partial u(x,t)}{\partial x}$$ \(ε\)は歪み、\(E\)は縦弾性係数(ヤング率)です。
運動方程式
上述のように応力や変位を表すと、棒の微小部分についての運動方程式は下記のように書けます。
応力\(σ\)はフックの法則から
なので、運動方程式は
棒の断面積が、\(x\)方向で一様であるとすると、\(A(x)=A\)となり、右辺の偏微分のカッコの中から外へ出すことができますね。
ここで\(c=\sqrt{\frac{E}{ρ}}\)と置くと、運動方程式は下記のようになります。
これは両端固定の弦の運動方程式(波動方程式)と同じ形ですね。
運動方程式が両端固定の弦と同じですので、一般解も全く同じ形になります。
まとめ
本日は棒の縦振動と横振動の説明と、縦振動についての運動方程式を解説しました。
運動方程式は両端固定の弦と同じ形になりますので、一般解も同じ形になります。
振動の波形は、境界条件等で決まってくるので、一般解へ代入することで求めることができます。
ポイントとしては『両端固定の弦と同じ形になる』ということを抑えておけば大丈夫です。
【縦振動についての解説】
振動・波動の基礎-㉘連続体の振動 棒の縦振動の具体例をわかりやすく解説
【横振動についての解説】
振動・波動の基礎-㉙連続体の振動 梁の横振動の運動方程式をわかりやすく解説
参考文献
- 振動工学の基礎:岩壺卓三、松久寛、森北出版株式会社
- 機械力学-振動の基礎から制御まで:日高照晃、小田哲、川辺尚志、曽我部雄次、吉田和信、朝倉書店
- 構造と連続体の力学基礎:熊でもわかる変形できる物体の力学:岩熊哲夫、小山茂 web版
初心者向けの振動工学の教科書・参考書をこちらで紹介していますので、参考にしていただければと思います。
初心者向けの教科書・参考書はこちら
振動工学の記事一覧はこちら
次の記事 →振動・波動の基礎-㉘連続体の振動 棒の縦振動の具体例をわかりやすく解説
