1次独立の関係とか行列式とかの関係性がよくわからないんだけど…


1次独立の条件は表し方がいくつかあって混乱しやすいから、今回は1つのパターンを解説するね。
今回は行列の基礎として、下記を学びます。
・1次独立と1次従属、行列式、逆行列、正則
この内容が出てくる分野としては、 振動の分野で、自由度が増えてくると固有振動モード算出のときに使います。
固有振動モードを導出する際には、上述の行列の計算が必須となってきますので、 本記事で理解できるように解説します。
行列とベクトルの掛け算の意味を理解していることが前提となりますので、よくわからない方は下記の過去記事を参考にしてください。
下記の動画でも解説していますので参考にしてください。
1次独立と1次従属
ポイント
- 1次独立:ベクトルが平行でない状態
- 1次従属:ベクトルが平行の状態
2次元の場合
まず、行列×ベクトルの計算を見てみましょう。
$$\left(\begin{array}{cc}1&2\\3&4\end{array}\right)\left(\begin{array}{c}1\\2\end{array}\right)=\left(\begin{array}{c}5\\11\end{array}\right)$$
ここで、行列Aとベクトル\(\vec{a}\)、\(\vec{b}\)を下記のように定義します。
$$A=\left(\begin{array}{cc}1&2\\3&4\end{array}\right)$$
$$\vec{a}=\left(\begin{array}{c}1\\2\end{array}\right)$$
$$\vec{b}=\left(\begin{array}{c}5\\11\end{array}\right)$$
さて、過去の記事でベクトル\(\vec{a}\)に行列Aをかけると異なるベクトル\(\vec{b}\)になる、ということを解説しましたが、 次にベクトル\(\vec{a}\)とベクトル\(\vec{b}\)の関係性について調べてみましょう。
$$\vec{a}=\left(\begin{array}{c}1\\2\end{array}\right)$$
$$\vec{b}=\left(\begin{array}{c}5\\11\end{array}\right)$$
図で書いてみると、下記のようになります。
こんな感じでそれぞれのベクトルが違う方向を向いていますね。
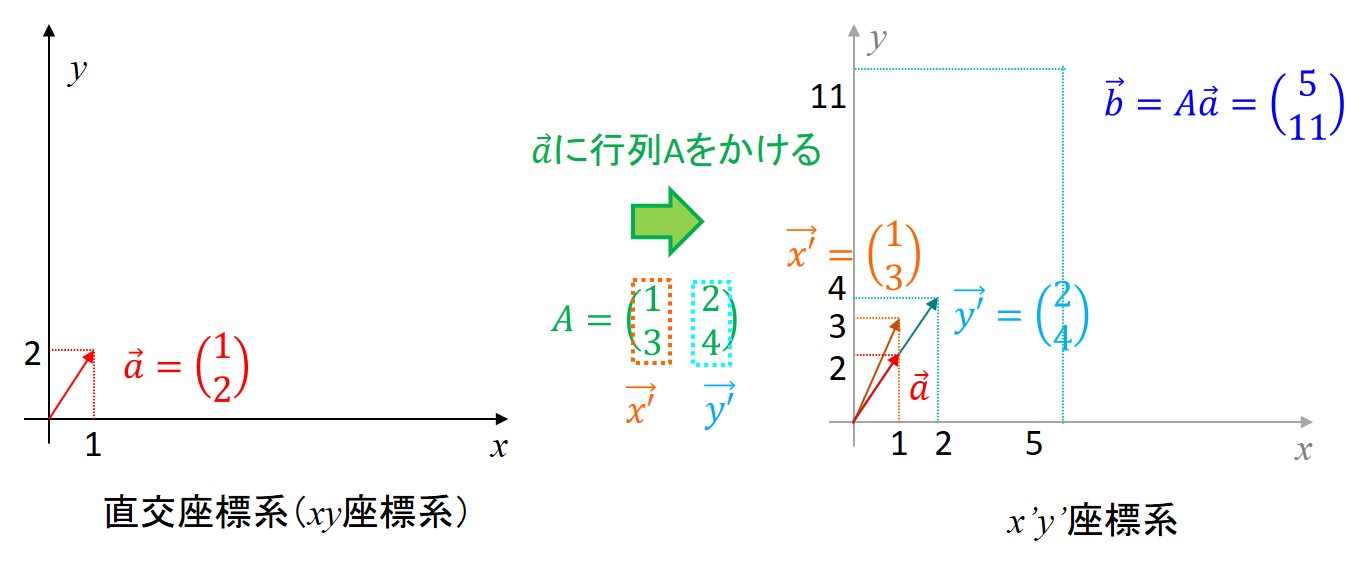
このように、違う方向に向いている状態を1次独立の関係にある、といいます。
ちょっとざっくりとしたな言い方なので、下記のような表し方をすることが多いです。
『aベクトルとbベクトルが定数倍しても表すことができないとき、1次独立の関係』といいます。
あるいは\(c_1,c_2\)をベクトルの係数として、\(c_1\vec{a}+c_2\vec{b}=0\)が成り立つのは、\(c_1=c_2=0\)のときのみである場合、1次独立である、と言います。
最後の表し方が教科書とかにも乗っている定義ですね。
いずれにしても、 ベクトルが平行かどうかで、1次独立か1次従属かがわかれます。
3次元以上の場合
3次元の場合は、ベクトルを3本(\(\vec{a_1},\vec{a_2},\vec{a_3}\))用意して、下図のように、3本のベクトルが同一平面上に無い場合、1次独立となります。
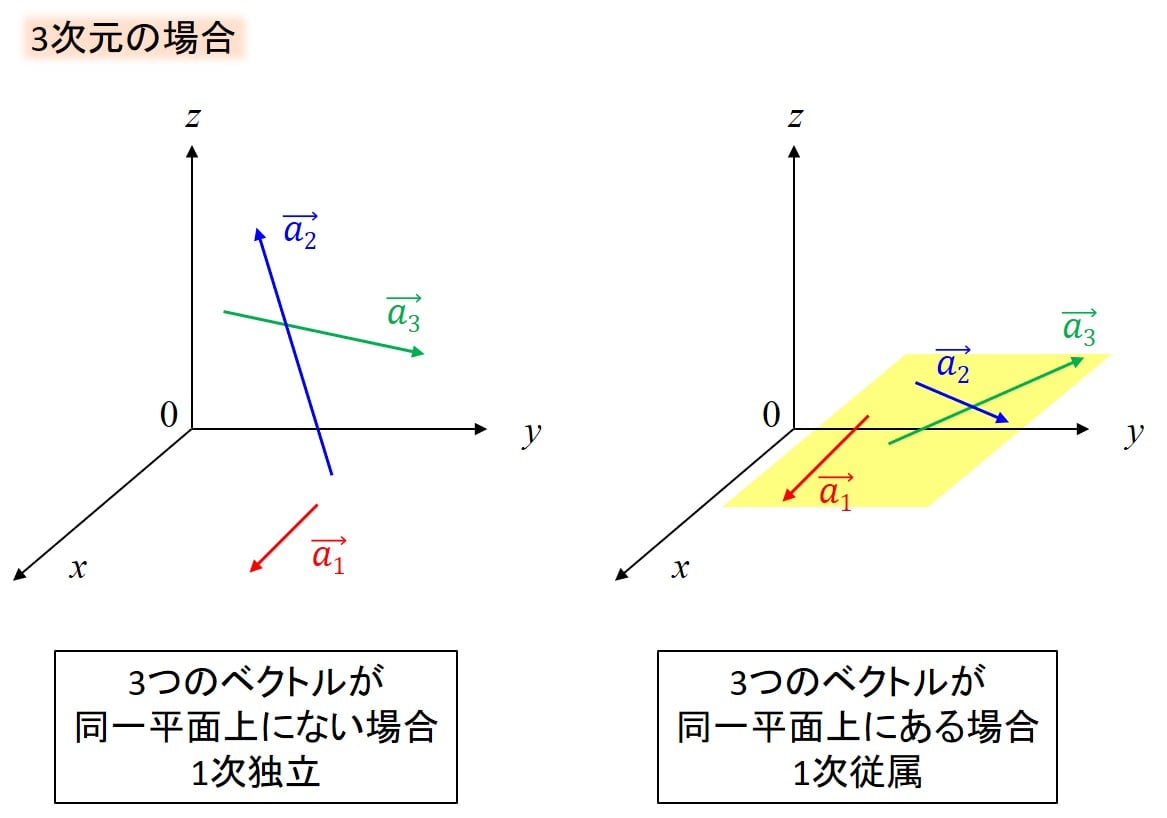
定義的には \(c_1\vec{a_1}+c_2\vec{a_2}+c_3\vec{a_3}=\vec{0}\)が成り立つのは、\(c_1=c_2=c_3=0\)のときのみである場合、1次独立であると言います。
n次元の場合 4次元以上は図に描くことができませんので、定義だけ示しておきます。
それぞれのベクトルの係数を\(c_i\)とし、\(i=1,2,3・・・n\)としますと、 \(c_1\vec{a_1}+c_2\vec{a_2}+c_3\vec{a_3}+…+c_n\vec{a_n}=\vec{0}\)が成り立つのは、\(c_1=c_2=c_3=…=c_n=0\)のときのみである場合、1次独立であると言います。
ちなみにこれは行列で書くこともできて、
$$(\vec{a_1},\vec{a_2},…\vec{a_n})\left(\begin{array}{cccc}c_1\\c_2\\\vdots\\c_n\end{array}\right)=0$$
このように書けて、\(c_1=c_2=c_3=…=c_n=0\)のときのみ成立する場合、1次独立となります。
さらにベクトル\(\vec{a_n}\)の成分を下記のように定義します。
$$\vec{a_n}=\left(\begin{array}{cccc}a_{n,1}\\a_{n_2}\\\vdots\\a_{n,n}\end{array}\right)$$
そうすると、先ほどのn次元の場合の1次独立の条件は下のように書けます。
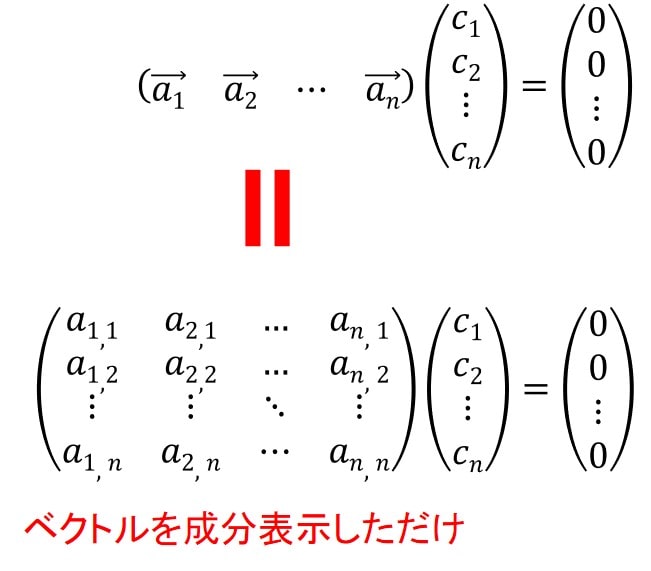
この式が成り立つのが\(c_1=c_2=c_3=…=c_n=0\)のみの時、\(\vec{a_1}、\vec{a_2}、…\vec{a_n}\)は1次独立と呼びます。
こういう形で突然出てくることもあるので、このように書けるということをしっかり理解しておきましょう。
行列式の意味
ここでも下記の設定を使いますね。
$$A\vec{a}=\vec{b}$$
$$A=\left(\begin{array}{cc}1&2\\3&4\end{array}\right)$$
$$\vec{a}=\left(\begin{array}{c}1\\2\end{array}\right)$$
$$\vec{b}=\left(\begin{array}{c}5\\11\end{array}\right)$$
最初に、 行列式は正方行列、つまりn行n列の行列のみに定義されますので、正方行列を前提に話を進めます。
このとき、Aの行列式は、一般的に下記のように書けます。
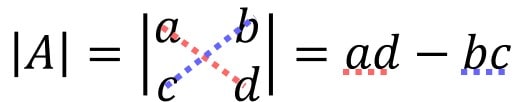
たすき掛けのようなイメージですね。今回の行列に当てはめると、
$$|A|=detA=1×4-2×3=-2$$
行列式は英語で"determinant"なので、行列式を表すときに\(det\)を前につけて表すことになっています。
さてこの行列式が、どういったことを意味しているのか?について説明していますね。
結論を先に示すと、 Aの行列式は直交座標系から行列の列ベクトルによって張られる座標系に変換したとき、 行列Aの列ベクトルに張られる平行四辺形の面積が何倍になったか、を示します。
図で書いたほうが分かりやすいと思うので、下図に示しますね。
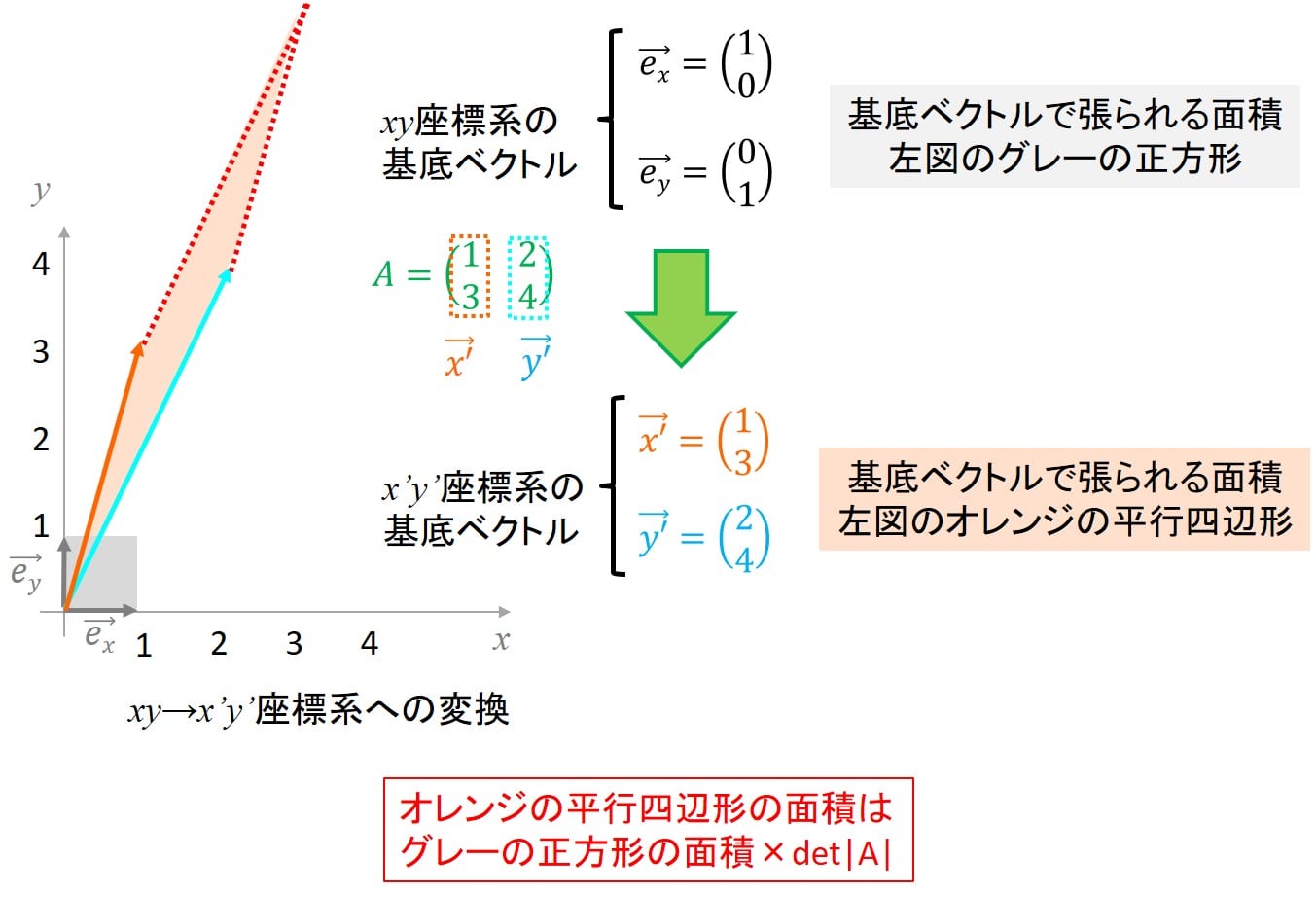
このように、座標系の基底ベクトルが変わったとき、張る面積が何倍になっているか、 を示しています。
ちなみにこれは2次元の場合なので面積となりますが、 3次元以上の場合、体積の倍率になります。
行列式がゼロの場合
これは、行列Aの列ベクトルが張る面積がゼロになるということなので、下記のような行列を考えましょう。
$$A=\left(\begin{array}{cc}1&1\\2&2\end{array}\right)$$
この場合、下図のような形になります。
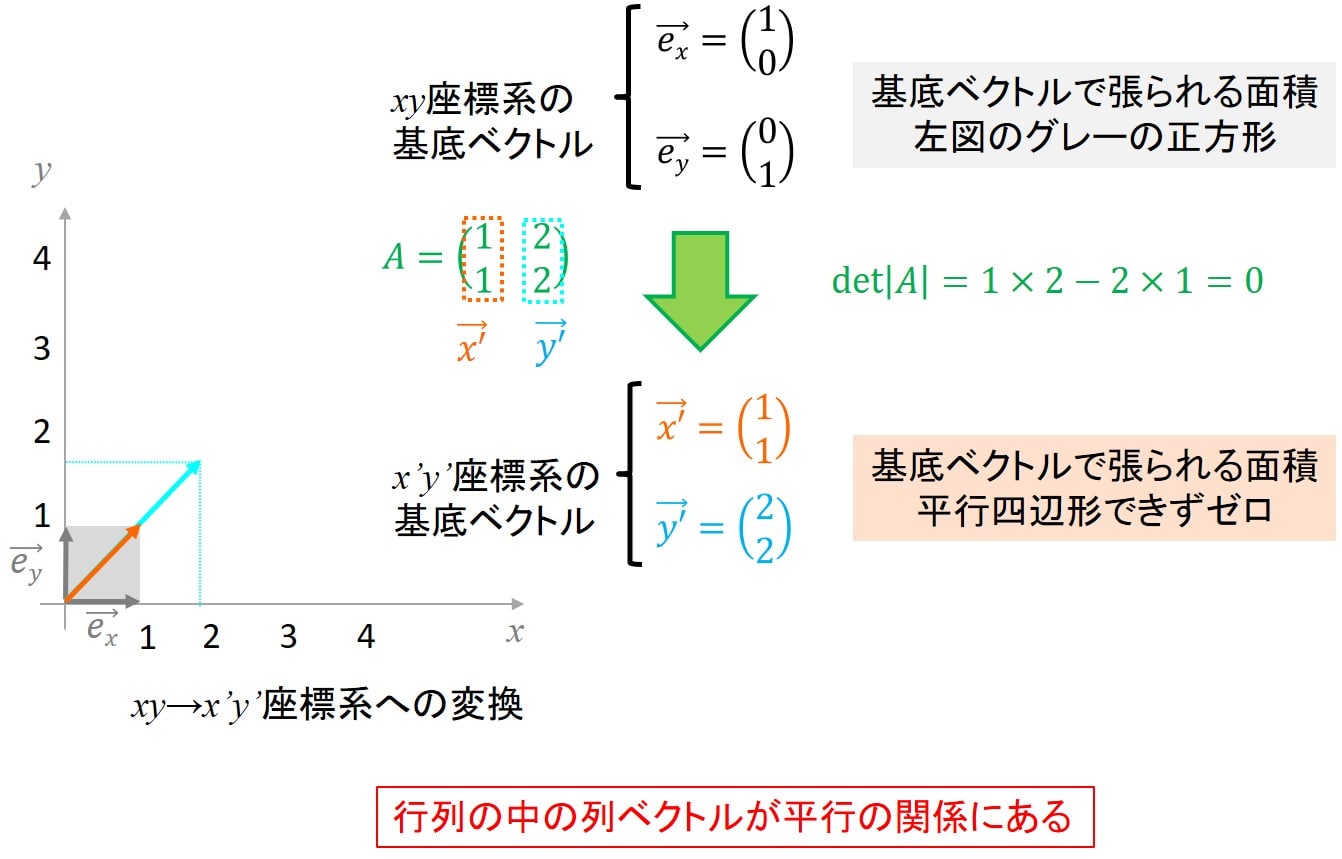
行列Aの列ベクトルが張る領域がライン上になってしまうわけですね。
このように行列Aの列ベクトルが平行の関係になってしまいますので、列ベクトル同士が1次従属の関係になっています。
行列Aの列ベクトルが1次独立か1次従属であるかどうかは、
- 行列式\(|A|=0\)のとき1次従属
- 行列式\(|A|≠0\)のとき1次独立
となります。
逆行列・正則について
もっとあっさりとした解説もあります。
逆行列という行列を使います。
行列Aの逆行列は、\(A^{-1}\)と書き、下記のような性質があります。
まず行列Aを下記のように2行2列の行列とします。
$$\left(\begin{array}{cc}a&b\\c&d\end{array}\right)$$
このとき逆行列は
$$AA^{-1}=A^{-1}A=E$$
\(E\)は単位行列で、
$$E=\left(\begin{array}{cc}1&0\\0&1\end{array}\right)$$
このような性質を持ちます。 逆行列は下記のように求めることができます。
$$A^{-1}=\frac{1}{ad-bc}\left(\begin{array}{cc}d&-b\\-c&a\end{array}\right)=\frac{1}{detA}\left(\begin{array}{cc}d&-b\\-c&a\end{array}\right)$$
逆行列は\(A\)の行列式で割っているため、逆行列が存在するためには、行列式\(detA≠0\)である必要があるわけですね。
また、逆行列をもつ行列のことを正則である行列(正則行列)と呼びます。
逆行列が存在するとどうなるか 同次方程式の連立方程式を行列表記すると、
$$\left(\begin{array}{cc}a&b\\c&d\end{array}\right)\left(\begin{array}{cc}x\\y\end{array}\right)=\left(\begin{array}{cc}0\\0\end{array}\right)$$ となります。
また、下記のように行列と、ベクトルを置きます。
$$A=\left(\begin{array}{cc}a&b\\c&d\end{array}\right), \vec{z}=\left(\begin{array}{cc}x\\y\end{array}\right),\vec{0}=\left(\begin{array}{cc}0\\0\end{array}\right)$$
そうすると、
$$A\vec{z}=\vec{0}$$
と書けます。
この行列\(A\)が逆行列を持ってしまうと、左側から\(A^{-1}\)をかけることで、 $$A^{-1}A\vec{z}=\vec{z}=\vec{0}$$
となってしまい、\(x=y=0\)が解となってしまいます。
つまり行列内のベクトルが1次独立になるわけですね。
そして、逆行列を持つ条件が行列式\(det|A|≠0\)なので、行列式\(det|A|≠0\)が1次独立である条件となるわけです。
まとめ
ポイント
- 1次独立:ベクトルが平行でない状態
- 1次従属:ベクトルが平行の状態
- 1次独立であるかどうかの条件
\(c_1a_1+c_2a_2+c_3a_3+…+c_na_n=0\)が成り立つのは、\(c_1=c_2=c_3=…=c_n=0\)のときのみである場合、1次独立
このときの行列Aが正則のとき、逆行列をもって1次独立。
正則である条件はAの行列式がゼロ Aの行列式は行列Aによって変換された基底ベクトルが張る空間の面積の倍率を示します。
行列式がゼロの場合、空間がつぶれる(次元が1つ落ちる)イメージです。
このため、同次方程式の連立方程式を仮定した時、解はバシッと1組に決まらず、比だけが求まります。
実は1次独立の条件の示し方は他にもあります(階数を使うなど)が、今回は省略します。
まずはこれらを理解しておけば、多自由度の振動の方程式が解けるようになりますので、しっかりとイメージを理解しておきましょう。
本記事で理解できなかった方は、下記の動画でも解説していますので参考にしてください。
