非線形のイメージはついたんですけど、なんで\(x^3\)で表されるの?

これまで、非線形力学の説明で、フックの法則に非線形項の\(x^3\)がつく、としてきました。
本日は、これがなぜ3乗の次数が出てくるのかについて説明します。
非線形力学の教科書とかでも、説明をすっ飛ばして急に3乗の項を入れてくることが多いです。
初学者がつまづきやすい点をできるだけわかりやすく解説していきますね。
非線形の高次の項とは?
結論を言うと、絶対に\(x^3\)となるというわけではない、です。
そもそも非線形って何??という方は下記の過去記事を参考にしてください。
参考記事
さて、冒頭にもあったように、このブログでも、他のサイトでも、非線形とは数式的には、
『\(x^3\)の項がくっついたもの』
と説明してきました。
これは ケースバイケースで、\(x^2\)だったり、\(x^4\)の項をつけて解析した論文もあります。
フックの法則もそうですが、経験則的によるところもあります。
2乗をつけることでうまく説明できたり、3乗でうまく説明できるものがあったり…
なんだよ、適当だったんなら、とりあえず使いやすい2乗とかでいいじゃん!

では、次にこの問いに答えていきましょう。
なぜ3次の項?
このブログでは両端固定梁の説明を多くしてきたからです。
両端固定梁の等価バネモデルを考えると、3乗の項が出てくるからです。
両端固定梁については下記で解説していますので、参考にしてください。
両端固定梁の等価バネモデル
等価バネモデルって何??という声が聞こえてきそうですので、下の図を見てください。
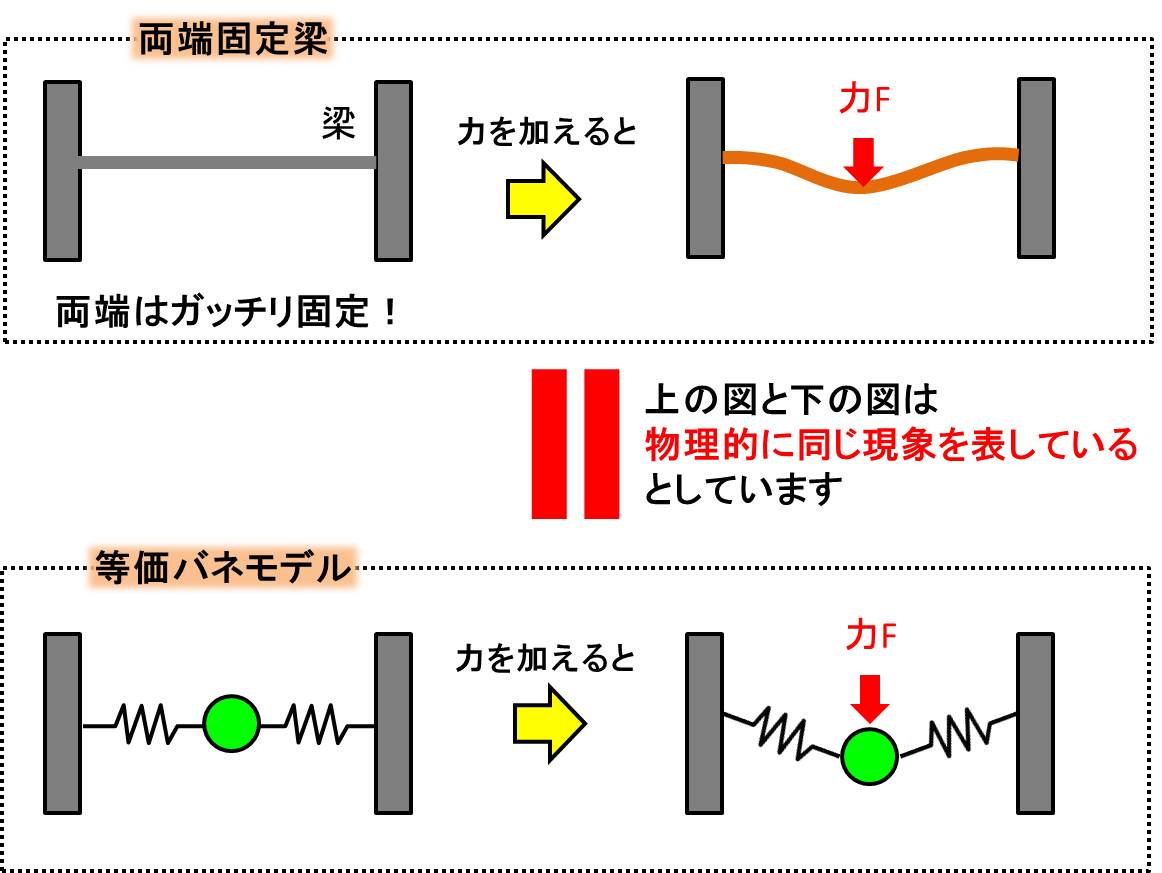
上側の両端固定梁は、下側のようなバネのモデルと同じことが起こっている、と考えます。
両端固定梁には梁の中央を押せば押すほど硬くなる、という性質があります。
(専門的にはハードニング、硬化型復元力と言います)
この硬くなる、というのは、両端固定梁の場合、
梁がたわむときに、梁自体が伸びなければいけない、
ということに由来しています。
モノが伸びるという現象は、応力とひずみの関係から、比例の関係にあります。
$$σ=E×ε$$
比例の関係にあるのであれば、同様のバネの式で表しても大丈夫です。
同様のバネの式とは…そう、フックの法則です。
$$F=k×x$$
梁が伸びる = バネが伸びる ということで置き換えているわけですね。
導出
ではこの等価モデルの場合、なぜ3次の項が出てくるのかについてです。
これは大学レベルの計算が必要ですので、計算が苦手な人は、
ちゃんと計算したら3次の項がでてくるんだ、と思って流してください。
まず、中央の物体が\(x\)だけ下側に変位したとき、物体がバネから受ける力を考えます。
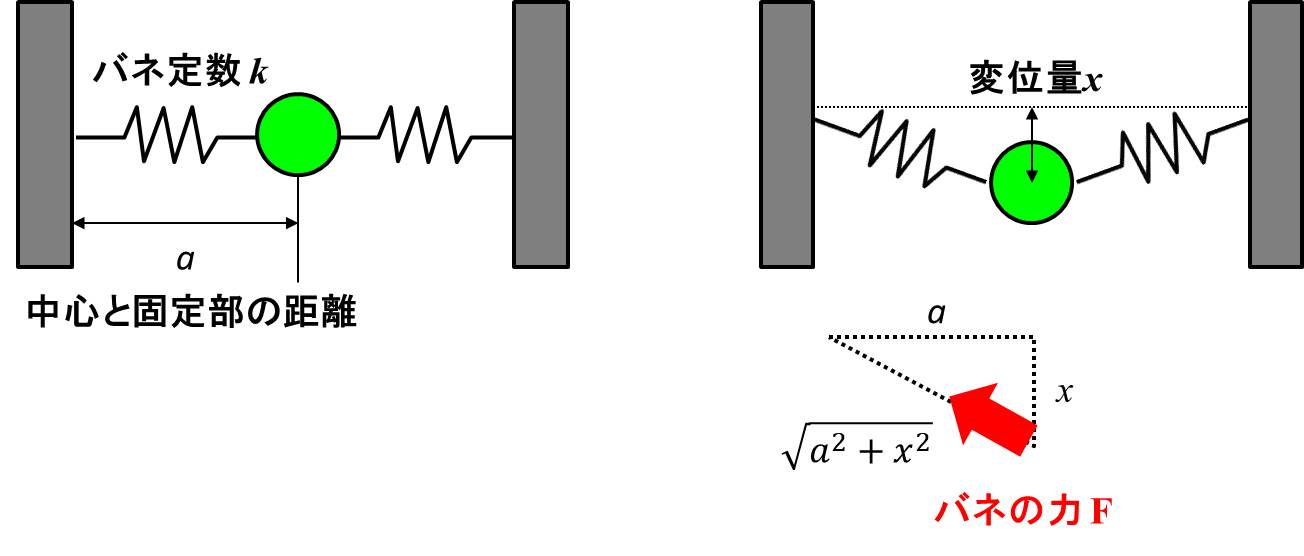
ここで、\(k\)はバネ定数、\(a\)は物体の中心と固定部の距離です。
バネの自然長は\(l\)としています。
つまり、最初の状態では、物体がバネから受ける力はゼロ、です。
変位させたときのバネの力は、直角三角形を考えます。
イメージとしては上図の赤矢印が、物体がバネから受ける力$F$ですね。
\(F\)の大きさは、フックの法則とバネの伸び量から、
$$F = k × (\sqrt{a^2+x^2})-l)$$
です。
では、これが図の上方向にどれくらいの力が発生しているかを計算します。
下の図の青の矢印の大きさ$F_0$を求めます。
これは直角三角形の相似の関係から計算できますね。
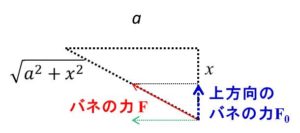
さきほどの\(F\)の式を代入すると
両側のバネから力を受けるので、2倍して整理すると
まだ3乗の項が出てきませんね。
実は\(x=0\)の周りでテイラー展開して近似することによって3乗の項が現れます。
テイラー展開は下記の式です。
\(f(x)=F_0\)とし、\(x_0=0\)として、テイラー展開してみると
となり、3乗の項が現れます。
これが両端固定梁の\(x^3\)の正体です。
注意点
3乗の項を出す際に、テイラー展開を使用しました。
テイラー展開は近似なので、条件を満たさなくなると成り立たなくなります。
変位量ゼロの周りでテイラー展開したので、あまり変位しないところでは$x^3$に従う、となります。
あまり変位しないところってどれくらいなの?という問いには、
これもケースバイケースです。どのような梁を使用しているかによって変わります。
まとめ
両端固定梁の非線形の3乗の項について解説しました。
バネの等価モデルから、受ける力を計算し、テイラー展開することで3乗の項は現れます。
ただし、テイラー展開という近似手法を使っているので、ある程度のところで近似から外れます。
テイラー展開の詳細の計算はまた別の記事で公開しようと思います。
この記事で少しでも非線形についての理解が深まれば幸いです。
参考文献
- 機械力学-振動の基礎から制御まで:日高照晃、小田哲、川辺尚志、曽我部雄次、吉田和信、朝倉書店
- 非線形力学(共立物理学講座6):戸田盛和、渡辺慎介、共立出版株式会社
- 振動工学の基礎:岩壺卓三、松久寛、森北出版株式会社
初心者向けの教科書・参考書はこちら
振動工学の記事一覧はこちら
