本記事では、共振の大きさを示すQ値について解説します。
過去に共振についてはこちらで解説していますので、そもそも共振って何??という方は、こちらをまず読んでくださいね。
この記事は下記のような人におススメです。
本記事をおススメする人
- 共振のイメージはわかったけど、Q値ってよくわかっていない人
- Q値をどのように導出するかわからない人
Q値とは
Q値とは、 共振ピークがどれだけ鋭く高くなるか、について示したものです。
共振を抑えるには減衰が効くということを示したましたが、Q値は減衰とふか~く関係しています。
イメージとしては下記のような感じです。
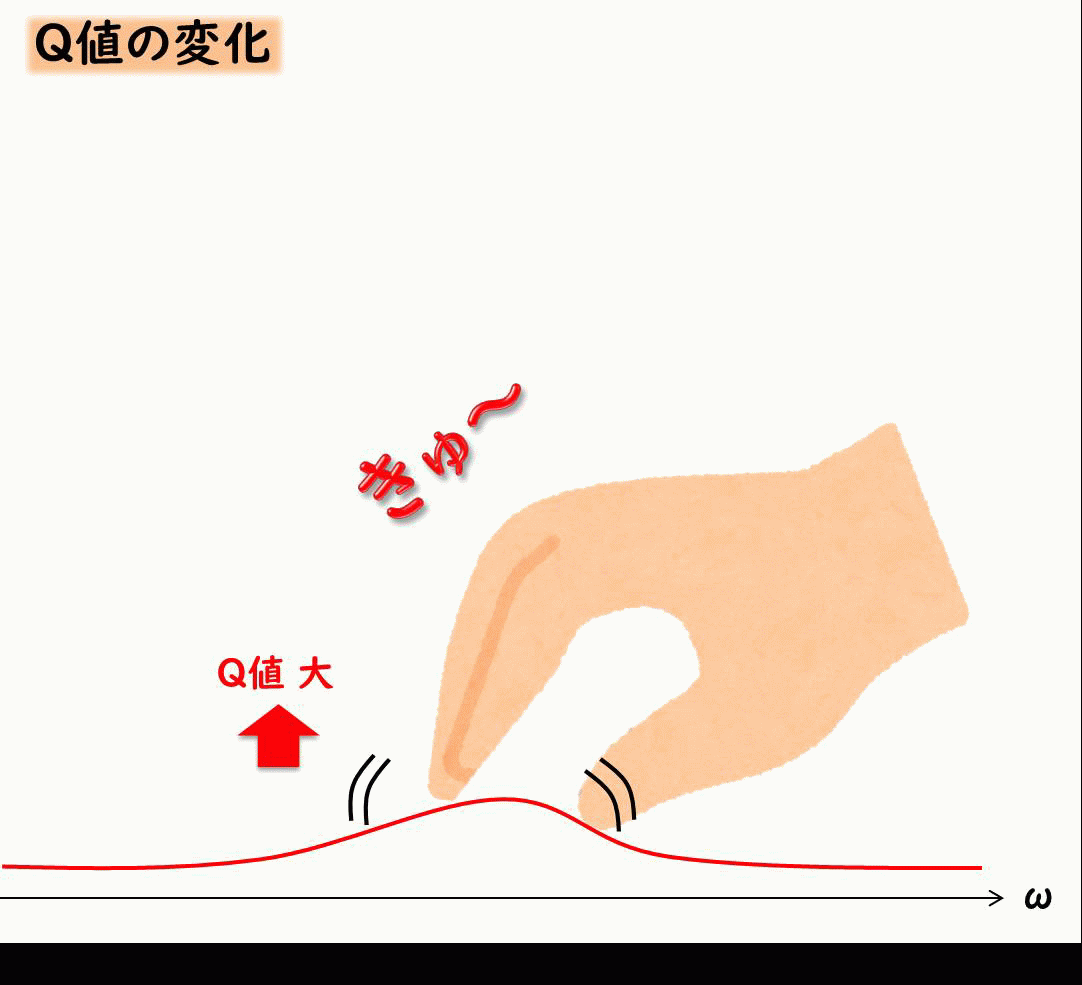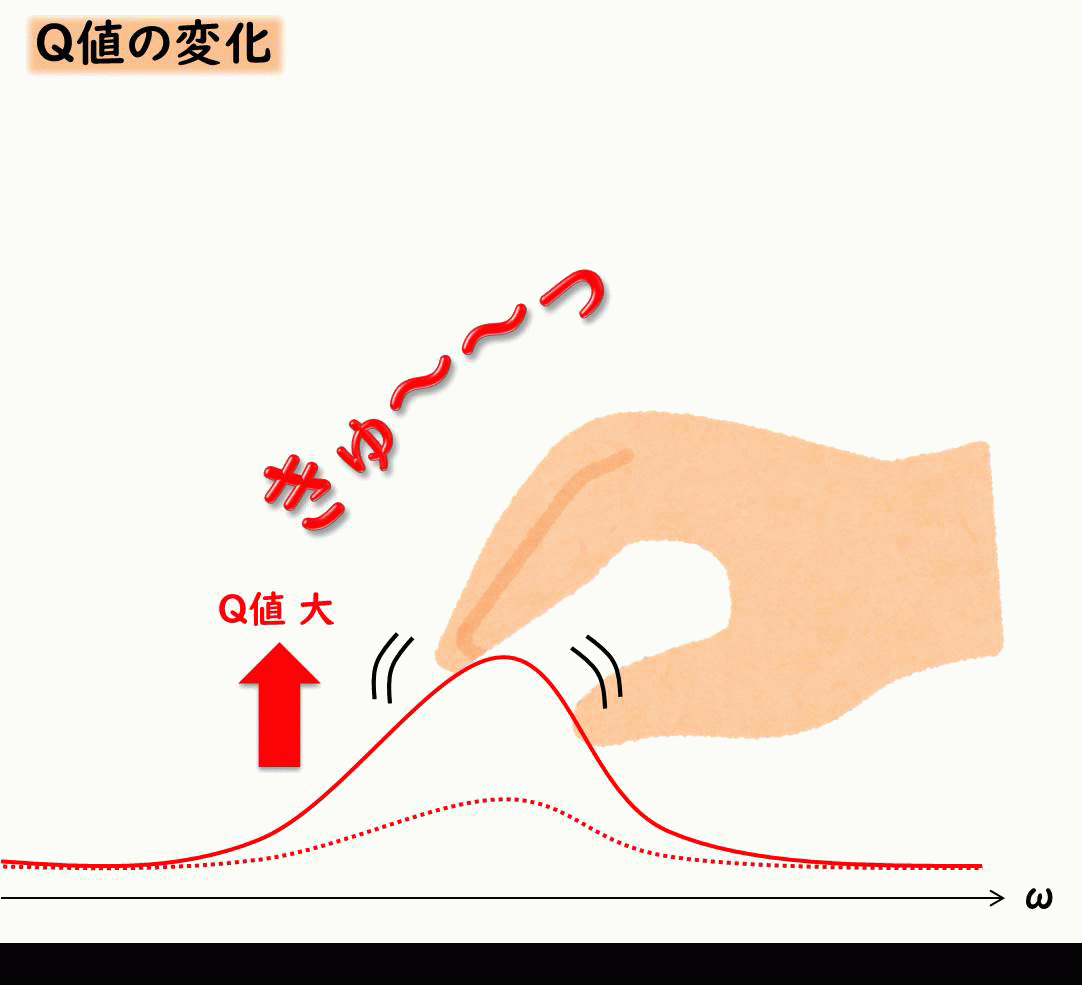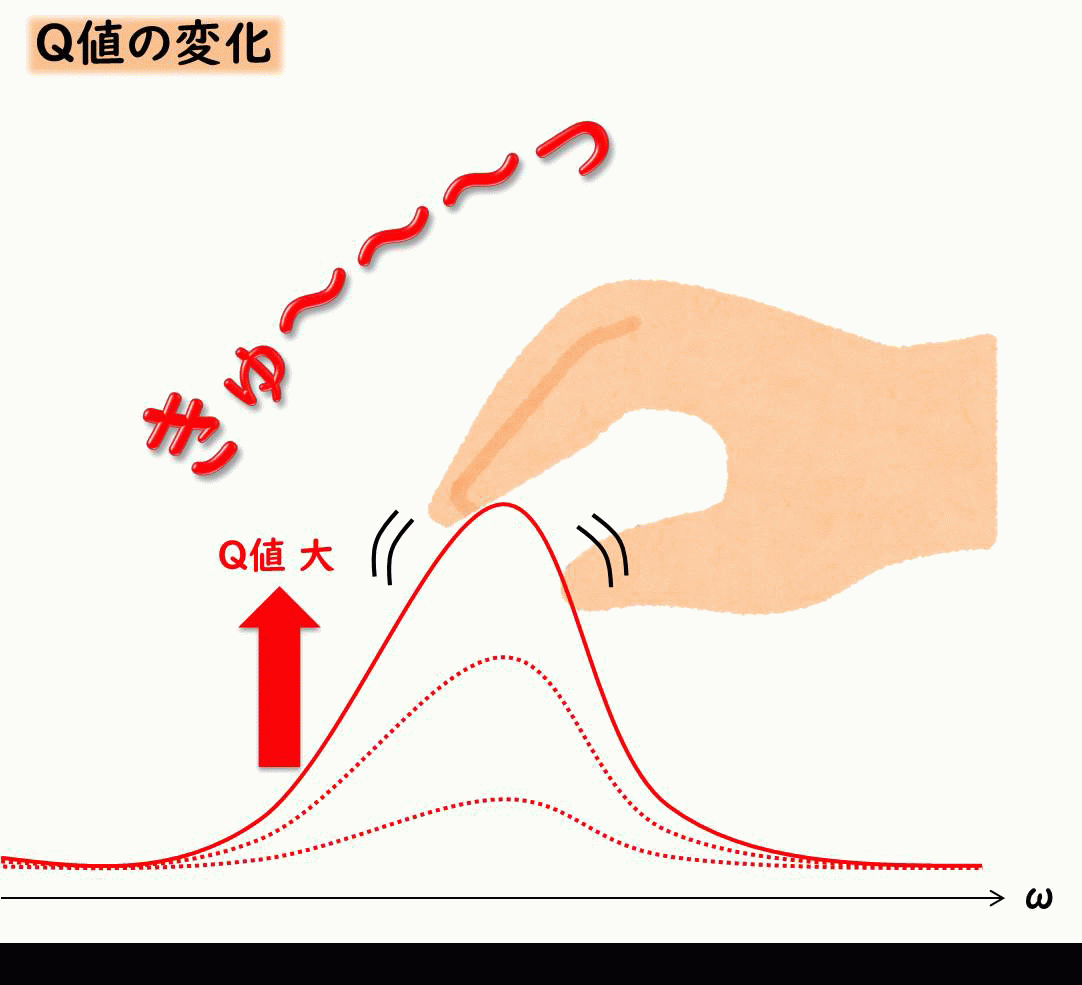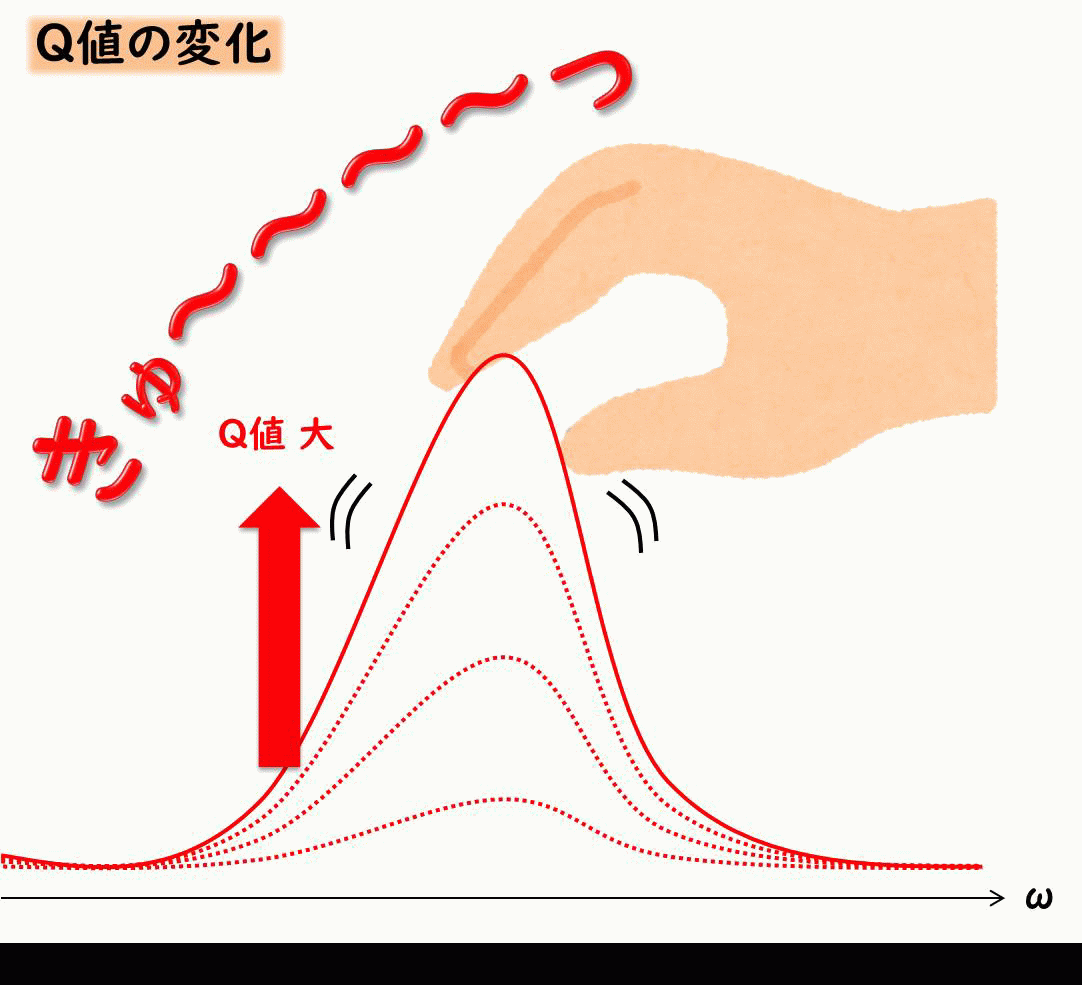
Q値は減衰比ζが小さい場合、
$$Q = \frac{1}{2ζ}$$
となります。
Q値の導出
このQ値の導出は、減衰のある強制振動の運動方程式を解く必要があります。
下記の記事で運動方程式を解いていますので、この部分は結果だけ引用します。
参考記事
減衰のある強制振動の運動方程式
下記のような物体がバネとダンパーに繋がれた質量に周期的外力が作用したモデルを考えます。
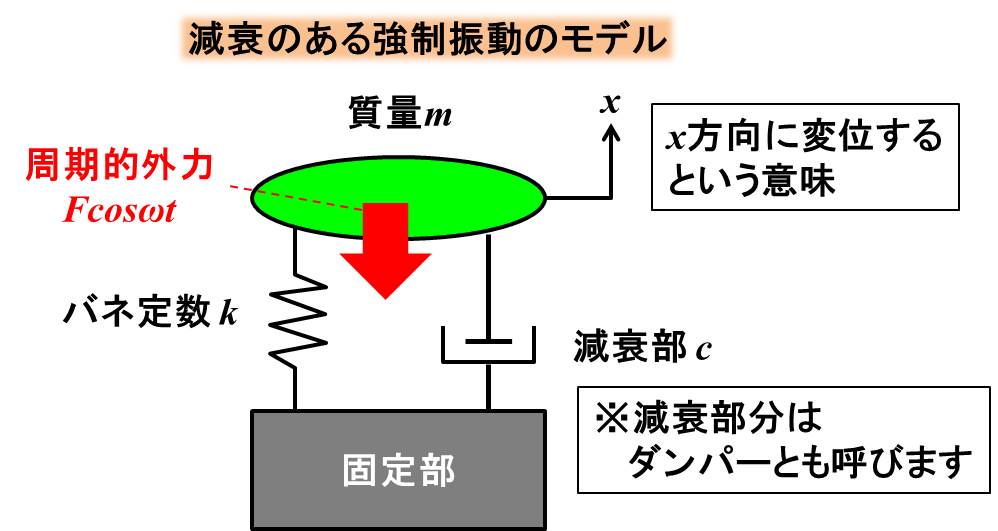
運動方程式は質量を\(m\)、減衰定数を\(c\)、バネ定数を\(k\)、周期的な外力\(Fcosωt\)とすると、下記のようになります。
$$m\ddot{x}+c\dot{x}+kx = Fcosωt$$
式を整理します。両辺\(m\)で割り、\(ζ、ω_0、f\)を使います。
$$\ddot{x}+2ζω_0\dot{x}+ω_0^2x-fcosωt =0$$
$$ζ = \frac{c}{2\sqrt{mk}}$$
$$ω_0 = \sqrt{\frac{k}{m}}$$
$$f =\frac{F}{m}$$
この運動方程式を解いて、共振時の振幅\(X_max\)と周波数\(ω\)は下記のようになります。
$$X_{max}=\frac{f}{2ζω_0\sqrt{(1-ζ^2}}・・・①$$
$$ω = \sqrt{1-2ζ^2}ω_0・・・②$$
この式の導出は面倒なので、過去記事を是非参考にしてください。
参考記事
Q値を算出する
Q値は共振ピークがどれだけ鋭く高くなるかを示したものになります。
どれくらい高くなるかを比率で考える必要があり、基準となるものが必要です。
その基準は周期的ではない外力をゆっくり与えたときの変位を基準としています。
ゆっくりというのは速さで減衰する項は無視して、外力Fを与えるということと同じです。
このとき、変位を\(X_{st}\)とすると、フックの法則の状態と同じになるから、
$$F = kX_{st} →X_{st}=\frac{F}{k}・・・③$$
ちなみにこれを静変位とも言います。
この値と下記の強制振動での共振ピークの高さの比をとります。
$$X_{max}=\frac{f}{2ζω_0\sqrt{(1-ζ^2}}・・・①$$
$$X_{st}=\frac{F}{k}・・・③$$
③式に\(k\)や\(F\)が入っていますので、
$$ω_0 = \sqrt{\frac{k}{m}}$$
$$f =\frac{F}{m}$$
を使って変形すると
$$X_{st}=\frac{f}{ω_0^2}・・・③'$$
よって、①を③'で割ると、
$$\frac{X_{max}}{X_{st}}=\frac{f}{2ζω_0\sqrt{(1-ζ^2}}×\frac{ω_0^2}{f}$$
$$\frac{X_{max}}{X_{st}}=\frac{1}{2ζ\sqrt{(1-ζ^2}}$$
共振ピークが発生するには\(ζ>\frac{1}{sqrt{2}}\)となる必要があり、小さければ小さいほど、ピークが高くなります。
ζがとても小さくてピークが発生するとき、つまり$ζ<<1$とすると
$$\frac{X_{max}}{X_{st}}≃\frac{1}{2ζ}$$
\(Q値 = \frac{1}{2ζ}\)が出てきました。
Q値は減衰比ζが小さいときの逆数となります。
ζが大きいとき、そもそもピークの高さが低くなるので、Q値そのものを議論する必要がない、ということですね。
\(ζ>\frac{1}{\sqrt{2}}\)とならなければピークが発生しないので、Q値は1以下になることはありません。
Q値をどのように使うか
構造設計の分野では

建物を構造設計する際、 共振というのは建物を破壊しうる危険な現象なので、気を付けなければいけません。
共振をできるだけ避けるために、 Q値をできるだけ低くなるように、というより、Q値を1以下にして共振が起こらないようにします。
電気回路の分野では
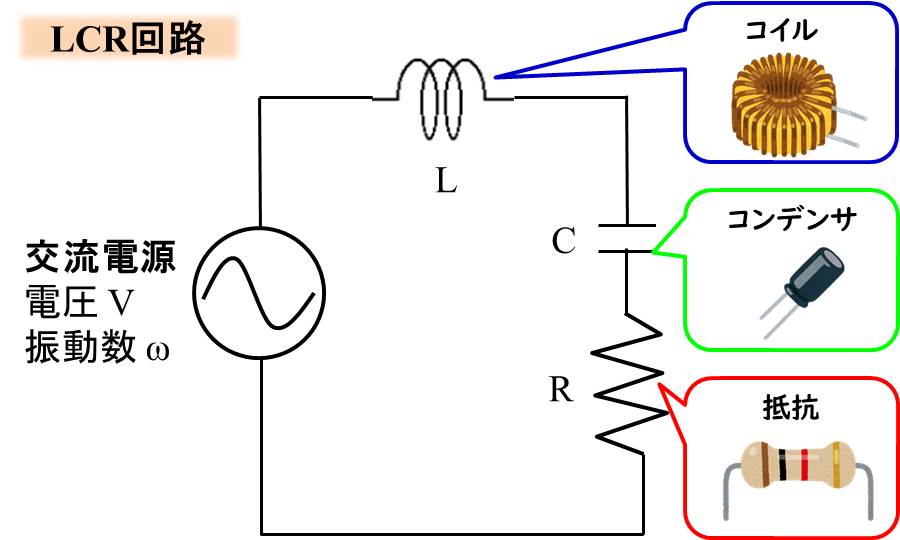
LCR共振回路というものがあり、この回路も共振現象が発生します。
回路で共振?と感じる方もいらっしゃるかと思いますが、コイル(L)とコンデンサ(C)と抵抗(R)をつないで回路を作って交流電源につなぐと、とある交流の周波数で共振が起こります。
つまり、交流では共振周波数でたくさんの電気が流れる、ということになります。
これを何に使うの??ということですが、
世の中には交流電流を流しても、単一の周波数で流れるということは非常に稀で、ノイズとして他の周波数成分が入ることが一般的です。
この ノイズを除去するフィルターの用途で、LCR回路を使います。
この回路を使えば、共振周波数以外の部分の周波数成分は、電気を流すことができなくなるのです。
で、 Q値の出番ですが、この回路ではQ値が高いほど、性能がよいフィルターになります。
つまり共振ピークが鋭く発生するほど、他の周波数成分が入ってこれない、単一の周波数成分だけ通すことのできるフィルター回路になる、というわけです。
フィルターの性能を表すのにQ値を使う、というわけですね。
まとめ
Q値の計算自体は、強制振動の運動方程式さえ解くことができればそれほど難しくないと思います。
Q値に関して重要なのは、ピークの鋭さを示す、ということと、どのような分野でどのように使われているか、を知ることです。
分野によってQ値は高い方がよいのか、小さい方がよいのか、変わってきますので、Q値のイメージをしっかりもって、使いこなしてほしいと思います。
参考文献
- 振動工学の基礎:岩壺卓三、松久寛、森北出版株式会社
- 機械力学-振動の基礎から制御まで:日高照晃、小田哲、川辺尚志、曽我部雄次、吉田和信、朝倉書店
- 構造と連続体の力学基礎:熊でもわかる変形できる物体の力学:岩熊哲夫、小山茂 web版
初心者向けの教科書・参考書はこちら
振動工学の記事一覧はこちら
