材料力学単純梁のBMD（曲げモーメント図）・SFD（せん断力図）を描く

片持ち梁のBMD・SFDは理解できたんだけど、単純梁の場合はどうしたらいいの？

苦手君

デルタ先生

やり方自体は片持ち梁と変わらないよ。境界条件とか少し違う部分もあるから、今日は単純梁について解説するね。

本日は単純梁の曲げモーメント図（BMD）・せん断力図（SFD）について解説します。

片持ち梁のBMD、SFDについては過去の記事で解説しています。

動画でも解説しておりますので、そちらも是非参考にしていただければとおもいます。

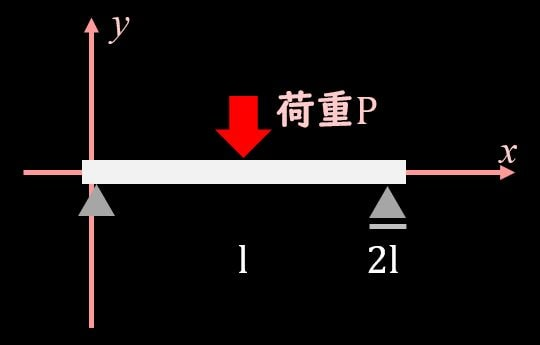
単純梁のモデル

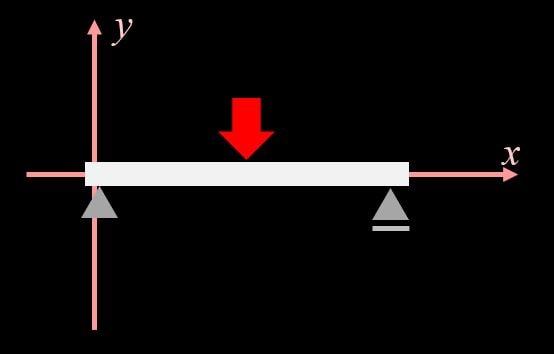
単純梁は上図のように、片側が単純支持（ピン支点）、もう片側がローラー支点となっている梁です。

教科書や人によっては両側ピン支点の梁のことを指す場合もあります。

いずれにせよ、支点の上に梁がポンっと乗っかっているイメージです。

今回はこの単純梁の中央に荷重Pをかけることを考えて行きましょう。

曲げモーメント図の書き方

片持ち梁の時と同じで、過去の記事で解説していますので、そちらもぜひ参考にしていただければと思います。

書き方としては5つのステップでした。

BMDの描き方

座標軸をとる
外力のつり合いの式を立てる
切り出して切り出した部分のせん断力を書く
せん断力によるモーメントを書く
切り出して面に注目して、せん断力によるモーメントにつり合うように、曲げモーメントを書く

まずひとつ目の座標軸を取る、ですが、単純梁の場合、下記のように座標軸をとることがほとんどですので、下記のモデルで2のつり合いの式を立てるところから進めて行きます。

つり合いを考える

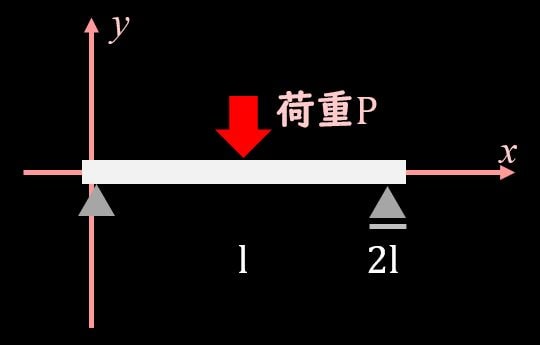
単純梁自体は大きさのある剛体になりますので、力のつり合いとモーメントのつり合いを考える必要があります。

長さ2lの梁のlの部分に荷重Pが発生しているとしますと、力のつりあいを成立させるために、支点からの反力を考える必要があります。

今回はピン支点とローラー支点の２つの支点があるわけですが、これらの支点が発生させることができる反力は下の表の通りです。

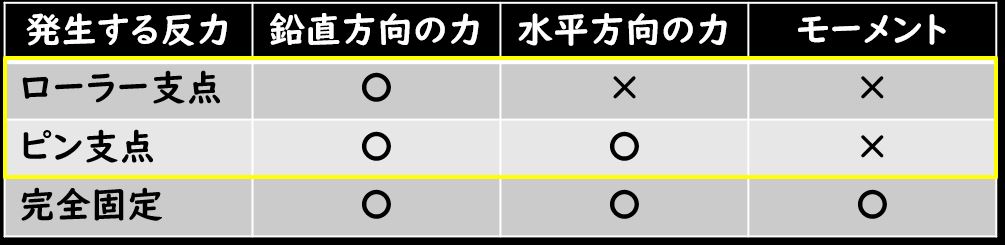
ピン支点の場合は、水平方向、鉛直方向に反力を発生させることができ、ローラー支点の場合は、鉛直方向のみ、力を発生させることができます。

今回は鉛直方向にしか力が発生していませんので、鉛直方向の力のつり合いを考えるわけですが、

ピン支点、ローラー支点の両方が鉛直方向の反力を発生させることができます。

左側の支点の反力を$R_A$、右側の支点の反力を$R_B$とすると、

$$P=R_A+R_B$$

という力のつり合いの式が成立します。

この式だけだと、未知数が反力の2つとなっているので、反力を求めることができません。

（片持ち梁の場合は反力は力のつり合いの式だけでも求まります）

単純梁の場合、モーメントのつり合いまで考えて、反力を決定する必要があります。

モーメントのつり合いを考えるのですが、荷重Pがかかっている点から考えると、

左側の支点にかかっているモーメントは、$R_A×l$、右側の支点にかかっているモーメントは、$R_B×l$となります。

ピン支点、ローラー支点はつりあうようにモーメントを発生させることができませんので、

これら２つのモーメントがつり合っている必要があります。

よって、

$$R_A×l=R_B×l$$

となって、$R_A=R_B$となります。

この式を用いると、力のつり合いの式は、

$$P=R_A+R_A$=2R_A$$

よって、

$$R_A=R_B=\frac{1}{2}P$$

と求めることができます。

切り出してせん断力を書く

材料力学は部材に発生する内力を考える学問ですので、部材を切り出し、切り出した部分の内力を考えて行きましょう。

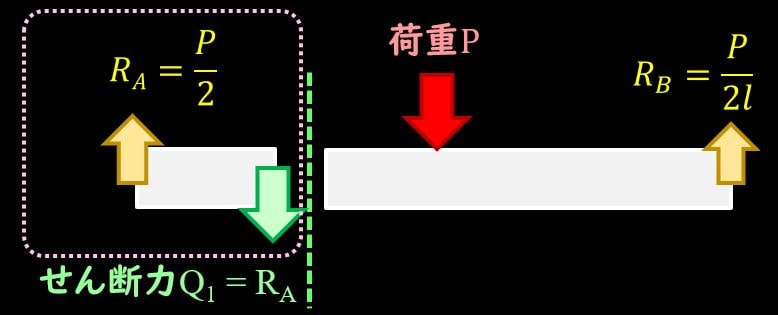
上図のように、荷重Pがかかっている左側のとある部分で切り出してみましょう。

ここでのポイントとしては、 切り出した部分にも力のつり合いが成立している、という点が重要でした。

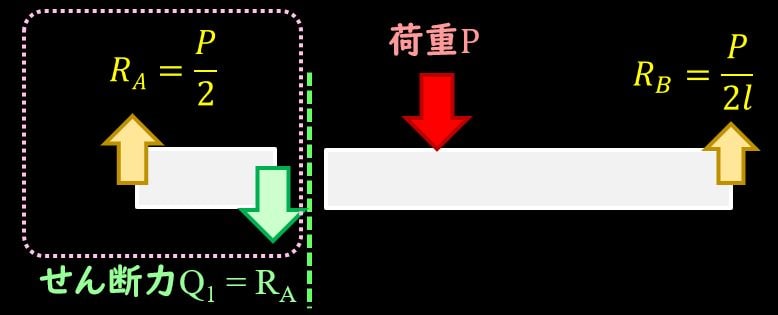
切り出した左側を見てみると、反力$R_A$が支点の部分に発生しており、この反力につりあう力が必要となります。

その力がせん断力$Q$で、

$$Q=R_A=\frac{1}{2}P$$

となります。

符号は下向きが正なので、正の向きにせん断力が発生しています。

さて、切り出した左側の部分はこうなりますが、切り出す位置を変えてみましょう。

下図のように、荷重がかかっている点より右側で切り出すことを考えます。

このときの切り出した左側の梁（点線で囲った部分）に発生しているせん断力を考えてみましょう。

切り出した部分に発生している力は2つですね。

反力$R_A$と荷重Pです。

反力$R_A=\frac{1}{2}P$でしたので、このままだと切り出した部分は力のつり合いが保てていません。

よって、切り出した面にせん断力が必要で、下図のように上向きにせん断力$Q$が発生します。

そのQの大きさは、力のつり合いを考慮すると、

$$Q=\frac{P}{2}-P=\frac{-P}{2}$$

となります。

以上を総合するとせん断力図SFDは下図のようになりますね。

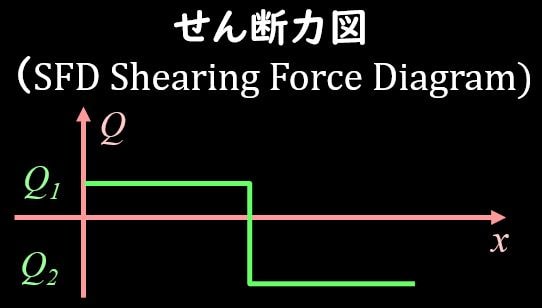
せん断力によるモーメントを考える

荷重がかかっている点の左側か右側かで、せん断力が変化していましたので、

せん断力によるモーメントも2パターンにわけて考える必要があります。

荷重より左側のモーメント

せん断力は下図のようになっていました。

この時、せん断力によるモーメントは、左端を支点とすると下図のように発生しますね。

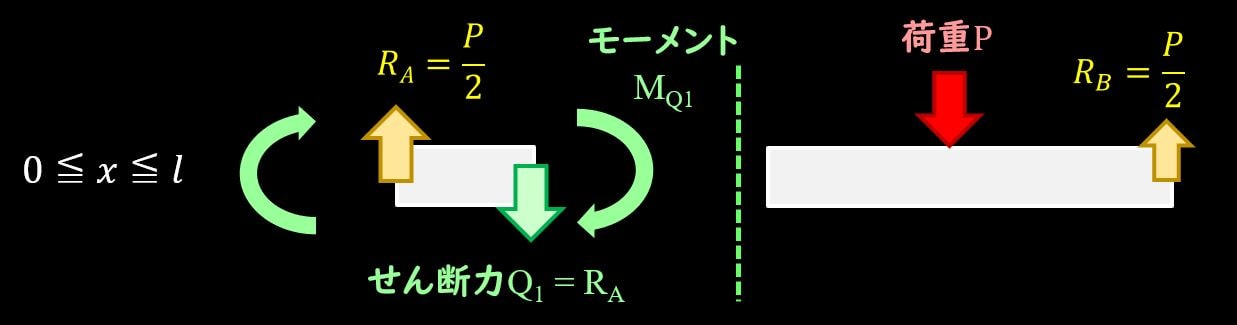
荷重より右側のモーメント

同様に、せん断力によるモーメントを左端を支点にして考えましょう。

すると下図ようにかけますね。

左端以外を支点にしてもいいの？

苦手君

デルタ先生

問題ないよ。最終的なモーメントつり合うように曲げモーメントを設定すればオッケーだよ。

曲げモーメントを求める

最後のステップとして、曲げモーメントを求めましょう。

これも荷重の左側を切った場合と右側を切った場合で場合わけが必要なので、それぞれを見て行きましょう。

荷重より左側の曲げモーメント

左端を支点としていますので、発生しているのはせん断力によるモーメントだけですね。

モーメントのつり合いが成り立つように、このモーメントと等しくなるように発生させたモーメントが曲げモーメントMですので、

$$M=Q×x=\frac{P}{2}x$$

となりますね。

荷重より右側の曲げモーメント

これも左端を支点としたときのモーメントを考えると、発生しているモーメントは下図ようになりますね。

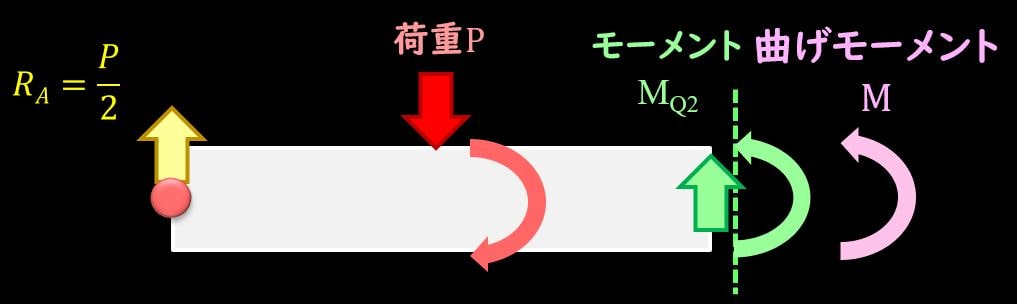
荷重によるモーメントとせん断力によるモーメントの２つとなります。

これら２つとつり合うように曲げモーメント$M$を発生させる必要がありますので、

$$M=P×l-Q×x=P(l-\frac{x}{2})$$

このように書き表すことができます。

まとめると、

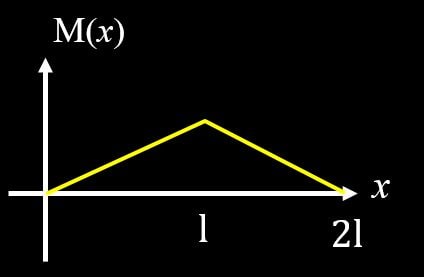
上図のようにBMDを描くことができます。

荷重をかける場所がl中央でない場合は？

これも同様の計算で求めることができます。

動画でも解説していますので、参考にしていただければと思います。

まとめ

単純梁のBMD、SFDの書き方について解説しました。

単純梁集中荷重のBMD

単純梁集中荷重の曲げモーメント