縦振動はわかったんだけど、横振動ってどうなるの?弦の振動と同じ?


横振動は縦振動の場合と少し異なるので、今日はまず梁の横振動について運動方程式を立ててみよう。
今日は梁の横振動について解説します。
これまで縦振動は棒で取り扱ってきましたが、今回は梁で解説します。
というのも、横振動は梁のような形状の方が議論しやすいからです。
(ちなみに縦振動は梁でも棒でも同じです)
縦振動については過去の記事で解説していますので、参考にしてください。
過去記事
梁の横振動全体について動画でも解説していますので、参考にしていただければと思います。
モデル
上図のような片持ち梁を考えましょう。
このような片持ち梁の微小部分を考えて、微分方程式を立てましょう。
上図のように、微小部分について\(x\)軸、\(y\)軸をとります。
運動方程式 \(y\)軸方向の運動方程式を考えてみましょう。
梁の密度を\(ρ\)、断面積を\(A\)、とすると、微小部分の質量は、\(ρ×A×dx\)となります。
次に、微小部分に発生している力とモーメントを考えましょう。
微小部分は剛体として取り扱うことができて、力の式と、モーメントの式の2つを考える必要があります。
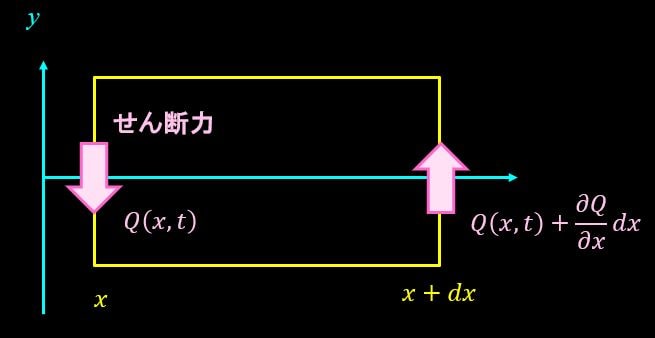
まず、左端に発生している力をせん断力\(Q(x,t)\)とすると、右端に発生しているせん断力は、
$$Q+\frac{\partial Q}{\partial x}dx$$
となります。
せん断力なので、左端と右端は向きが逆になっていることに注意してください。
よって、運動方程式は、
$$ρAdx\frac{\partial^2 y(x,t)}{\partial t^2}=Q+\frac{\partial Q}{\partial x}dx-Q=\frac{\partial Q}{\partial x}dx$$
となります。
ここで、未知のせん断力\(Q(x,t)\)を曲げモーメントの式を使うことで、梁のパラメータで表現することを考えます。
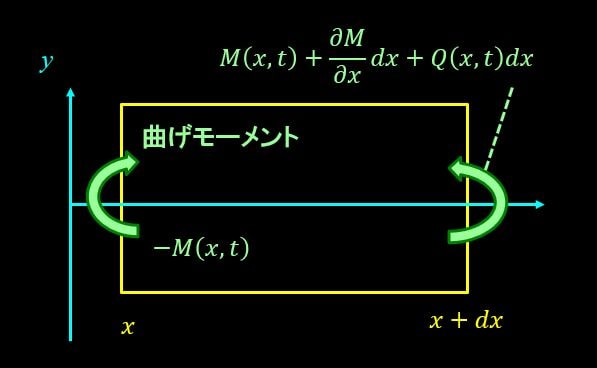
モーメントのつり合いの式から、
$$M(x,t)+\frac{\partial M}{\partial x}dx-M(x,t)+Q(x,t)dx=0$$
整理すると、
$$\frac{\partial M}{\partial x}=-Q$$
これを運動方程式に代入すると、
$$ρAdx\frac{\partial^2 y(x,t)}{\partial t^2}=-\frac{\partial^2 M}{\partial x^2}dx$$
曲げモーメントは材料力学の知識から下記のように変位との関係を表すことができて、
$$EI\frac{\partial^2y}{\partial x^2}=M$$
ここで\(E\)はヤング率、\(I\)は断面2次モーメントです。
この式を運動方程式に代入すると、
$$ρAdx\frac{\partial^2 y(x,t)}{\partial t^2}+\frac{\partial^2 }{\partial x^2}\left(EI\frac{\partial^2y}{\partial x^2}\right)=0$$
梁の材質や形状が長さ方向に一定であれば、\(EI\)、\(A\)は定数となるので、偏微分の前に出せて、
$$ρAdx\frac{\partial^2 y(x,t)}{\partial t^2}+\frac{\partial^4y }{\partial x^4}=0$$
このように、梁の横振動については、4階微分が出てくるような高階の微分方程式となります。
まとめ
今回は梁の横振動の運動方程式を立て方を解説しました。
弦の振動や縦振動と異なり、4階の偏微分方程式になっていることに注意しましょう。
これに伴い、一般解の形もこれまでと異なる形になりますので、次回は自由振動の一般解を解説しますね。
参考文献
- 振動工学の基礎:岩壺卓三、松久寛、森北出版株式会社
- 機械力学-振動の基礎から制御まで:日高照晃、小田哲、川辺尚志、曽我部雄次、吉田和信、朝倉書店
- 構造と連続体の力学基礎:熊でもわかる変形できる物体の力学:岩熊哲夫、小山茂 web版
初心者向けの振動工学の教科書・参考書をこちらで紹介していますので、参考にしていただければと思います。
初心者向けの教科書・参考書はこちら
振動工学の記事一覧はこちら
次の記事 →振動・波動の基礎-㉚連続体の振動 梁の横振動の運動方程式の一般解をわかりやすく解説
