振動のエネルギーって勉強する必要あるの?これまで通り変位の式とかから振動の状態ってわかるんじゃない?


正直、見たい現象によるところはあるんだけど、エネルギーの観点で見たほうが分かりやすいものもあるから、エネルギーもしっかり勉強したほうがいいよ。
本日は振動のエネルギーについて勉強します。
身近な例として地震の大きさのマグニチュードという単位も、 揺れのエネルギーを示しています。
エネルギーの観点から考えることによって、『見ている振動の大きさ』というものがわかりやすくなりますので、しっかりと理解しておきましょう。
今回は基礎編として、単振動と減衰ありの自由振動を取り扱います。
下記は単振動のエネルギーについて解説した動画なので、是非参考にしてみてください。
単振動の場合
単振動のモデルと運動方程式
単振動のモデルは上記のように、質点がバネにつながれて同じペースで同じ大きさで揺れ続けている状態ですね。
運動方程式は、質量を\(m\)、バネ定数\(k\)とすると、
$$m\ddot{x}=-kx$$
となります。
この単振動の変位の式は下記のように表すことができます。
$$x = Asin(ωt+Φ)$$
横軸を時間\(t\)、縦軸を変位\(x\)としたグラフは下記のようなグラフになります。

時間とともに上下に波打って変位しているのがわかりますね。
この変位の式の導出は、過去の記事や下記の動画を参考にしていただけばと思います。
振動・波動の基礎①-2 単振動の運動方程式を解く 変位の式はなぜ三角関数?
単振動のエネルギー
エネルギーの種類は下記の2種類になります。
- 運動エネルギー \(V\)
- バネの弾性エネルギー \(U\)
運動エネルギー\(V\)、弾性エネルギー\(U\)はそれぞれ下記のようになります。
$$V=\frac{1}{2}m\dot{x}^2$$
$$U=\frac{1}{2}kx^2$$
二つの和が振動の力学的エネルギーEに相当し、和を取ってみると下記のようになります。
$$E=V+U=\frac{1}{2}m\dot{x}^2+\frac{1}{2}kx^2$$
ここで、変位の式は\(x = Asin(ωt+Φ)\)なので、上式に代入すると、
$$E=\frac{1}{2}mA^2ω^2cos^2(ωt+Φ)+\frac{1}{2}kA^2sin^2(ωt+Φ)$$
2項目のkは\(ω^2=\frac{k}{m}\)なので、\(mω^2\)となり、下記のように表されます。
$$E=\frac{1}{2}(mω^2A^2(cos^2(ωt+Φ)+sin^2(ωt+Φ))$$
\(cos^2(ωt+Φ)+sin^2(ωt+Φ)=1\)なので、
$$E=\frac{1}{2}mω^2A^2$$
振動のエネルギーは質量×振幅の2乗×角振動数の2乗 となりますので、質量、振幅、周波数が大きいほどエネルギーが大きくなることが分かります。
揺れが大きくても、周波数(揺れるスピード)が小さいとエネルギーは小さくなるのは想像しやすいですね。
減衰振動の場合
減衰振動のエネルギーについても下記の動画で解説していますので、参考にしてください。
減衰振動のモデルと運動方程式
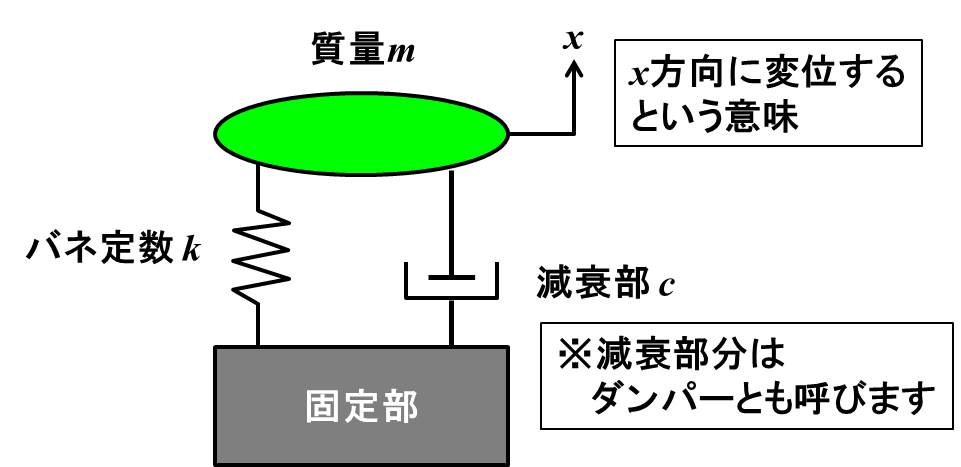
減衰振動のモデルは上記のように、質点がバネとダンパーにつながれている状態ですね。
運動方程式は下記のようになります。
$$m\ddot{x}+c\dot{x}+kx=0$$
この減衰振動の変位の式は下記のように表すことができます。
$$x=e^{-ζωt}Asin(ω_dt+Φ)$$
$$ω_d = ω\sqrt{1-ζ^2}$$

振幅が徐々に小さくなっていくような振動ですね。
この振動のエネルギーについて考えてみましょう。
減衰振動のエネルギー
運動エネルギー\(V\)、弾性エネルギー\(U\)はそれぞれ下記のようになります。
$$V=\frac{1}{2}m\dot{x}^2$$
$$U=\frac{1}{2}kx^2$$
これらをそれぞれ計算しましょう。
運動エネルギー
$$V=\frac{1}{2}m\dot{x}^2$$
$$x=e^{-ζωt}Asin(ω_dt+Φ)$$
\(x\)を微分すると、
$$\dot{x}=-ζωe^{-ζωt}Asin(ω_dt+Φ)+ω_de^{-ζωt}Acos(ω_dt+Φ)$$
くくって整理すると、
$$\dot{x}=e^{-ζωt}A(-ζωsin(ω_dt+Φ)+ω_dcos(ω_dt+Φ))$$
ここで三角関数の合成を行って、
$$\dot{x}=e^{-ζωt}A(\sqrt{ω_d^2+(ζω)^2}sin(ω_dt+Φ+Φ_0)$$
$$tanΦ_0=\frac{ω_d}{-ζω}$$
\(ω_d = ω\sqrt{1-ζ^2}\)なので、
$$\dot{x}=e^{-ζωt}Aωsin(ω_dt+Φ+Φ_0)$$
この式をVの式に代入すると、下記のようになります。
$$V=\frac{1}{2}me^{-2ζωt}A^2ω^2sin^2(ω_dt+Φ+Φ_0)$$
バネの弾性エネルギー
$$U=\frac{1}{2}kx^2$$
この式に\(x=e^{-ζωt}Asin(ω_dt+Φ)\)を代入します。
$$U=\frac{1}{2}ke^{-2ζωt}A^2sin^2(ω_dt+Φ)$$
減衰振動の力学的エネルギー
それでは力学的エネルギーを計算しましょう。運動エネルギー\(U\)と弾性エネルギー\(V\)の和を取ると、
2項目の\(k\)は\(ω^2=\frac{k}{m}\)なので、\(mω^2\)となり、まとめることができて、
$$E=\frac{1}{2}mω^2A^2e^{-2ζωt}(sin^2(ω_dt+Φ+Φ_0)+sin^2(ω_dt+Φ))$$
$sin^2$については下記の三角関数の公式を使って整理します。
$$sin^2θ=1-cos^2θ=1-\frac{1+cos2θ}{2}=\frac{1-cos2θ}{2}$$
よってEは
$$E=\frac{1}{4}mω^2A^2e^{-2ζωt}(2-cos2(ω_dt+Φ+Φ_0)-cos2(ω_dt+Φ))$$
今度は\(cos\)の2項に下記の和積の公式を使います。
$$cosx+cosy=2cos\frac{x+y}{2}cos\frac{x-y}{2}$$
この和積の公式を使って整理すると、
$$E=\frac{1}{2}mω^2A^2e^{-2ζωt}(1-cos2(ω_dt+Φ+Φ_0)cosΦ_0)$$
\(cosΦ_0\)の\(Φ_0\)は三角関数の合成で現れた角度で、
$$tanΦ_0=\frac{ω_d}{-ζω}、cosΦ_0=\frac{-ζω}{\sqrt{ω_d^2+(ζω)^2}}$$
\(ω_d = ω\sqrt{1-ζ^2}\)なので、\(cosΦ_0\)の分母は\(ω\)になって、
$$cosΦ_0=-ζ$$
となります。
よって力学的エネルギーEは下記のようになります。
$$E=\frac{1}{2}mω^2A^2e^{-2ζωt}(1+ζcos2(ω_dt+Φ+Φ_0)$$
エネルギーの式に\(e^{-2ζωt}\)が入っているので、減衰振動では時間が経過すると指数関数的にエネルギーが小さくなっていく形になっています。
散逸関数
減衰振動ではエネルギーが小さくなっていくのがわかったところで、
このエネルギーが逃げていく現象を表す散逸関数\(D\)というものを考えてみましょう。
力学的エネルギーの時間変化を考えるために、Eを時間微分してみると、
$$\frac{dE}{dt}=\frac{dV}{dt}+\frac{dU}{dt}$$
個別に計算すると、
$$\frac{dV}{dt}=m\dot{x}\ddot{x}$$
$$\frac{dU}{dt}=kx\dot{x}$$
よって、
$$\frac{dE}{dt}=m\dot{x}\ddot{x}+kx\dot{x}=\dot{x}(m\ddot{x}+kx)$$
ここで、運動方程式は、
$$m\ddot{x}+c\dot{x}+kx=0$$
この式を代入して、
$$\frac{dE}{dt}=\dot{x}(-c\dot{x})=-c\dot{x}^2$$
散逸関数\(D\)を
$$D=\frac{1}{2}c\dot{x}^2$$
と定義すると、
$$\frac{dE}{dt}=-c\dot{x}^2=-2D$$
散逸関数は ダンパーによってエネルギーが系から消失していることを示します。
まとめ
今回は振動のエネルギーについて解説しました。
振動の力学的エネルギーを考える際は、運動エネルギーとバネの弾性エネルギーの和をとればよく、
振動のエネルギーは質量、振幅、周波数に依存します。
また減衰を考慮することで、振動エネルギーが系から減少していきます。
この減衰による振動エネルギーの消失を表すのが散逸関数\(D\)というものでした。
振動のエネルギーの観点から考えることで、振動の大きさのイメージがわかりやすくなると思いますので、
是非エネルギーの観点から考えられるようになりましょう。
参考文献
- 振動工学の基礎:岩壺卓三、松久寛、森北出版株式会社
- 機械力学-振動の基礎から制御まで:日高照晃、小田哲、川辺尚志、曽我部雄次、吉田和信、朝倉書店
- 振動・波動:小形正男、裳華房
- 構造と連続体の力学基礎:熊でもわかる変形できる物体の力学:岩熊哲夫、小山茂 web版
初心者向けの振動工学の教科書・参考書をこちらで紹介していますので、参考にしていただければと思います。
初心者向けの教科書・参考書はこちら
振動工学の記事一覧はこちら
次の記事 → 振動・波動の基礎 強制振動のエネルギー
