固有振動モードの勉強していたら、モード合成っていう単語がでてきたんだけど、これって何?


モード合成は固有振動モードを考えるときに、とても大事な考え方になるから、ちゃんと理解できるように説明するね。
今回はモード合成についてです。
固有振動モードについてこれまで学習してきましたが、この固有振動モードの重要な性質がモード合成という概念になります。
固有振動モードについて詳しく知りたい方は下記の過去の記事を参考にしてください。
参考記事
本記事をおススメする人
- 多自由度の振動を勉強している人
- 振動のモード合成について知りたい人
- 物理を勉強していて興味がある人、仕事で振動の知識を使う人
モード合成とは
モード合成とは、振動の解をそれぞれのモードの重ね合わせで表現する方法、です。
N自由度の振動は、自由度が多すぎて複雑になってしまうのですが、もっと単純化して考えれるようにする方法がモード合成なのです。
固有振動モードの復習
過去の記事でも固有振動モードの導出を取り扱っていますので参考にしていただければと思います。
前回は減衰無し、外力無しのN自由度の振動を取り扱っていました。
-min.jpg)
まずは復習しましょう。この運動方程式は、
$$[M]\{\ddot{X}\}+[K]\{X\}=0\tag{1}$$
\([M]\)、\([K]\)はそれぞれ質量マトリックス、弾性マトリックスで、\(\{X\}\)は位置のベクトルです。
この運動方程式の一般解は
$$\{x\}=\sum_{r=1}^N\{x^r\}=\sum_{r=1}^NC_r\{u^r\}sin(ω_rt+φ_r)\tag{2}$$
\(r\):固有振動モードの次数
\(\{x^r\}\):r次の変位を表すベクトル
\(x_i^r\)というのは\(r\)次の固有振動における、\(i\)番目の質量の変位を表しています。
\(\{u^r\}\):r次の変位を表すベクトル
\(\{u^r\}=\left(\begin{array}{c}u_1^r\\u_2^r\\\vdots\\u_N^r\end{array}\right)\)
\(u_i^r\)というのはr次の固有振動における、i番目の質量の振幅を表しています。
\(ω_r\):r次の固有振動数
\(φ_r\):r次の初期位相
\(C_r\):定数
運動方程式を解いて、固有振動数\(ω\)や固有振動モードを示す\(\{u_r\}\)を求める必要があるのですが、
運動方程式の中の剛性マトリックス\([K]\)の中に非対角項(連成項)が存在するため、N次連立方程式を解かなければいけなくなり、計算がややこしくなります。
そのため、対角化できるような座標系に座標変換することで、N次連立方程式から、N個の独立した方程式に書き換えることを前回行いました。
座標変換した座標系をモード座標と呼ぶのでしたね。
この時、座標変換するための変換マトリックスを\([Φ]\)とすると、\([Φ]\)は\(\{u^r\}\)を並べたもので表現できるので、下記のように表すことができます。
$$Φ=[\{u^1\},\{u^2\},・・・\{u^r\}・・・\{u^N\}]$$
この[Φ]を使って、$\{X\}$を座標変換すると、
$$\{X\}=Φ\{ξ\}$$
と表すことができます。
\(\{X\}\)を座標変換し、運動方程式(1)の左側から\(Φ^{-1}\)を作用させて、係数のマトリックスを対角化すると、下記が得られます。
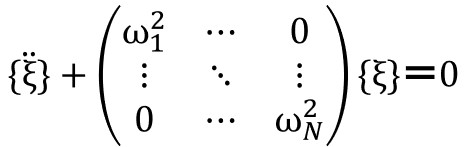
ここまでが前回の復習です。
モードの合成
この\(\{ξ\}\)についてもう少し詳しく見ていきます。
$$\{X\}=Φ\{ξ\}$$
という関係があり、この変換マトリックス\(Φ\)を書き下してみます。
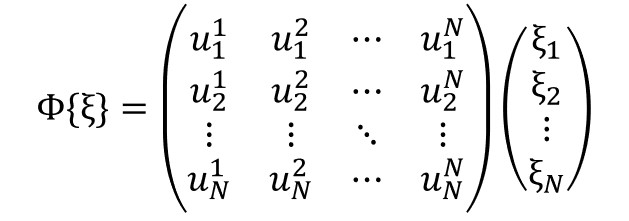
これを計算しまとめると、
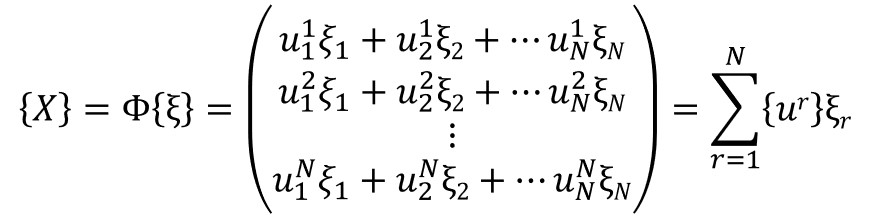
このように書き直せます。
\(\{X\}=\{x\}\)のとき、一般解となるので、この式そのものが解になるわけです。
この中身を見てみると、各質点の運動が固有モード\(ξ\)の足し合わせになっています。

このように、座標変換した固有モードの座標系でも、各固有モードの足し合わせで振動を表現できる、というようにするのが、モード合成です。
実はこれは座標変換する前に、解を固有モードの重ね合わせで表せる、と仮定しているので、当たり前といえば当たり前の結果ですね。
実際にみてみると、運動方程式の一般解は下記のような(2)式で表される、と仮定しています。
これは一般解が1次~N次までの固有モードの線形結合、要するに足し合わせで表されている、ということを意味しています。
モード合成のメリット
さて、モード座標でも各固有振動モードの足し合わせで解を記述できる、ということを示したのですが、これのメリットについて解説します。
Nが2とか3とかだったら、すべて計算して足し合わせして求めることができます。
でも、Nが100とか1000とか、もっと多かったら??
実際の複雑な物体、たとえば車を表現するには、点は1000点で足りるでしょうか?
試しに車を点だけで書いてみることを考えると、
リアルな車にするには、無数の点が必要になるわけです。
そんなとき、モード合成法を取り入れます。
固有振動数をモード座標で求めると、固有振動数が低い方から順番に1次、2次・・・という風にしていくわけで、
Nが100だったら100次の固有振動数が出てくるわけです。
で、この固有振動数と一致した振動が外力として入ってくると、共振してしまうわけです。
でも実は、100次の固有振動数って大抵はめちゃくちゃ高い振動数になるのです。
実際に考える必要がある振動数の範囲というのはある程度決まっているわけで、そこから外れためちゃくちゃ高い振動数の領域は無視できます。
例えば地震とかは数Hzの周波数と言われていますので、地震に対する設計で1000Hz以上の固有振動を考えてもあまり意味がないのです。
ということで、N=100のとき、100次まで考える必要はなく、10次とか20次とかまで考えれば十分で、
それに伴い計算量も各段に少なくなるのです。
これがモード合成によるメリットです。
まとめ
モード合成について解説しました。
振動の解として固有モードの重ね合わせで表現できるのは、モード座標変換しても成立します。
モード座標に変換することで、独立した方程式を解けばよくなりますし、解も重ね合わせるだけで表現できるので、
不要な次数の固有振動の成分は無視して計算することで、計算量を各段に少なくできることを説明しました。
振動に関する設計者は是非理解しておきたい内容ですので、しっかり概念を覚えておきましょう。
参考文献
- 振動工学の基礎:岩壺卓三、松久寛、森北出版株式会社
- 機械力学-振動の基礎から制御まで:日高照晃、小田哲、川辺尚志、曽我部雄次、吉田和信、朝倉書店
- 構造と連続体の力学基礎:熊でもわかる変形できる物体の力学:岩熊哲夫、小山茂 web版
初心者向けの振動工学の教科書・参考書をこちらで紹介していますので、参考にしていただければと思います。
初心者向けの教科書・参考書はこちら
振動工学の記事一覧はこちら
次の記事 → 振動・波動の基礎-㉒モード合成について 固有振動モードを重ね合わせる!
