固有振動モードって結局、振動数方程式を解いたら求まるんだったらそれでいいんじゃない?


その通りなんだけど、振動数方程式から固有振動数を計算するのはかなりしんどいんだ。
かなりしんどいって?確かに2自由度でも結構計算量多かったけど…


まぁ正攻法でやると人の手じゃほぼ無理だね。計算を簡単にする方法があるから、今日はその方法を学んでいこう。
今日は固有振動モードの導出です。
行列の操作がたくさん入ってきますが、できるだけわかりやすく解説します。
前回、多自由度の運動方程式を解いて、一般解を計算していますので、そちらも参考にしてください。
過去記事
本記事をおススメする人
- 多自由度の振動を勉強している人
- 固有振動モードの計算をしたい人
- 物理を勉強していて興味がある人、仕事で振動の知識を使う人
取り扱うモデル
-min.jpg)
今回取り扱うモデルは、前回と同じく減衰無しN自由度の連成振動です。
i=1,2,3,・・・,Nとして、
\(m_i\):\(i\)番目の質点の質量
\(k_i\):\(i\)番目のバネのバネ定数
\(x_i\):\(i\)番目の質点の位置
となります。
運動方程式と一般解
運動方程式は、
$$[M]\{\ddot{X}\}+[K]\{X\}=0\tag{1}$$
[M]、[K]はそれぞれ質量マトリックス、弾性マトリックスで、\(\{X\}\)は位置のベクトルです。
この運動方程式の一般解は
\(r\):固有振動モードの次数
\(\{x^r\}\):\(r\)次の変位を表すベクトル
\(x_i^r\)というのは\(r\)次の固有振動における、i番目の質量の変位を表しています。
\(\{u^r\}\):\(r\)次の変位を表すベクトル
\(\{u^r\}=\left(\begin{array}{c}u_1^r\\u_2^r\\\vdots\\u_N^r\end{array}\right)\)
\(u_i^r\)というのは\(r\)次の固有振動における、\(i\)番目の質量の振幅を表しています。
\(ω_r\):\(r\)次の固有振動数
\(φ_r\):\(r\)次の初期位相
\(C_r\):定数
振動数方程式を解くというのは、行列式がゼロの同次方程式を解くことになるので、r次における振幅の絶対値は求まらず、各質量の振幅の比が求まります。
したがって振幅に定数$C_r$をかけることになります。
固有振動数の求め方
この固有振動数が非常に重要で、どうにかして簡単に求めたいのですが、振動数方程式をもう一度見てみると、
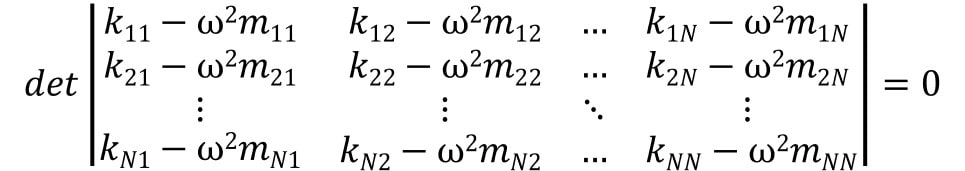
これを満たすようなωを考えると\(ω^2\)のN次方程式がN個連立して並ぶことになります。
これは少々キツイ計算になることが予想されますので、行列を簡単にすることを考えます。
この行列式の出どころは、(1)の運動方程式から求まっていて、
\(\{X\}=\{u\}sinωt\)と基本解をおいたときに、
\(\{\ddot{X}\}=-ω^2\{u\}sinωt\)となるので、運動方程式は
$$([K]-ω^2[M])\{u\}=0\tag{3}$$
これが\(u_i=0\)以外の解をもつための条件が行列式なわけです。
ということで、この(3)式を構成する\([K]、[M]\)の中をもう少し詳しく見てみると、

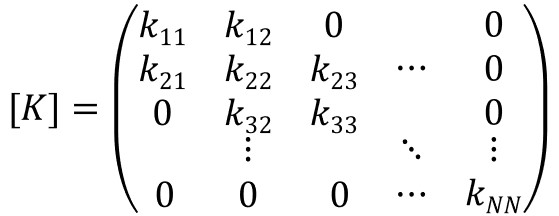
それぞれの行列の中身はこのようになるわけです。
[M]は対角行列になっていますが、[K]は隣り合うバネの影響を表現するため、非対角項が残っています。
\(k_{12}\)とか\(k_{32}\)の項が非対角項ですね。これらは連成項と呼ぶのでした。
この連成項があることが厄介なんです。
試しに\([K]\{u\}\)を見てみると、
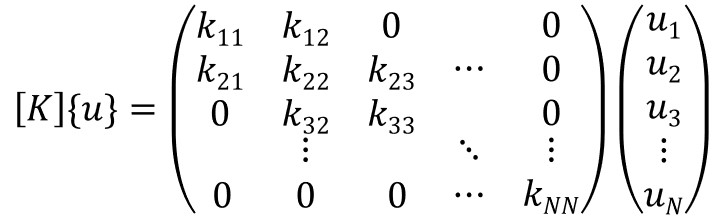
これを1行目の計算をしてみると、図の赤枠部分の掛け算なので、

$$k_{11}u_1+k_{12}u_2+0×u_3・・・$$
という形になりますね。
1行目の計算に\(u_1\)と\(u_2\)が入っています。
こうなると右辺をゼロとしたときに、
$$k_{11}u_1+k_{12}u_2=0$$
という式になるのですが、式が1つに未知数2つなので解けません。
じゃあ2行目の式と連立すればいいじゃん!と思っても、2行目の式は下の図の赤枠の掛け算なので、

右辺をゼロにした式は、
となって、未知数として\(u_3\)が増えてしまい、また解けなくなります。
じゃあ、3行目の式・・・としてみても、今度は\(u_4\)が出てきて・・・ということを繰り返してしまい、
結局N個の未知数に対するN個の連立方程式を解くことになってしまいます。
この恐ろしい数の連立方程式を解かなければいけなくなるのは、連成項が存在するためなんです。
じゃあこの連成項を消去する方法を考えて、計算を楽にしましょうよ、と考えるわけです。
連成項がなくなった行列は、対角行列と呼びます。(\([M]\)も対角行列です)
対角行列にすることを線形代数学では対角化、と呼ぶんでしたね。
ここで、例えばAという行列を対角化するためには、変換行列[P]を使うと、
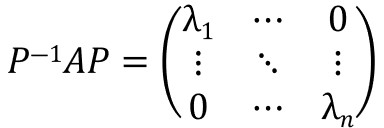
と表されます。
λは行列Aの1次独立な固有ベクトル\(\{x_1\}\)、\(\{x_2\}\)、・・・\(\{x_n\}\)に対応する固有値です。
で、変換行列\([P]\)の作り方ですが、これは1次独立な固有ベクトルを並べた行列になるのでした。
つまり、\(P=[x_1,x_2,・・・,x_n]\)という行列になります。
まず、\(([K]-ω^2[M])\{u\}=0\)の左側から\([M]^{-1}\)をかけて、\(([M]^{-1}[K]-ω^2[E])\{u\}=0\)という形にして、一般固有値問題に帰着させます。
大学の線形代数で学んだよくある固有値問題に変形する、ということをしています。
今回、\([A]=[M]^{-1}[K]\)とすると、\([A]\)を対角化するような変換行列\(Φ\)は、固有値\(ω^2\)に対する、固有ベクトル\(\{u^r\}\)を並べればよいので、
と表すことができます。
この変換行列\(Φ\)と逆行列\(Φ^{-1}\)で\([A]\)を挟むことを考えると、もとの方程式は、
$$[A]\{u\}=0$$
なので、まず左から\(Φ^{-1}\)をかけると、
$$Φ^{-1}[A]\{u\}=0$$
ここで、右から\(Φ\)をかけると\(\{u\}\)の右側からかけてしまうので、\([A]\)のすぐ右側に\(Φ\)が出てくるように下のようにします。
$$Φ^{-1}[A]ΦΦ^{-1}\{u\}=0$$
逆行列との積は単位行列になるので、このように変形しても問題ないわけです。
\(\{q\}=Φ^{-1}\{u\}\)とすると、
$$Φ^{-1}[A]Φ\{q\}=0$$
このいきなり出てきた$\{q\}$ですが、これは一般化座標で、\(\{u\}\)に変換行列をかけたもの、つまり変換行列によって座標変換されたものになります。
さらに言い換えると\(\{u\}\)で表されるような実座標空間から、行列をかけることで別の座標空間に変換した、という操作になります。
この座標空間に変換することで、係数の行列が対角化された状態になるので、一般化されたqの座標空間で考えた方が計算が楽になるわけですね。
もう少し厳密に\(\{X\}=\{u\}sinωt\)としていたので、
\(\{q\}=\{ξ\}sinωt\)とすると、\(\{ξ\}=Φ^{-1}\{X\}\)となります。
このときの\(\{ξ\}\)をモード座標といいます。このモード座標系で考えるとマトリックスが対角化されて計算が楽になります。
運動方程式に戻って、
$$[M]\{\ddot{X}\}+[K]\{X\}=0\tag{1}$$
左側から\([M]^{-1}\)を作用させて、
$$\{\ddot{X}\}+[M]^{-1}[K]\{X\}=0$$
\([A]=[M]^{-1}[K]\)を使うと、
$$\{\ddot{X}\}+[A]\{X\}=0$$
左側から\(Φ^{-1}\)を作用させて、\(\{ξ\}=Φ^{-1}\{X\}\)より\(\{X\}=Φ\{ξ\}\)使って変換すると、
$$Φ^{-1}Φ\{\ddot{ξ}\}+Φ^{-1}[A]Φ\{ξ\}=0$$
対角化した行列\(Φ^{-1}[A]Φ\)は固有値\(ω^2\)を対角化成分にもつ行列になるので、
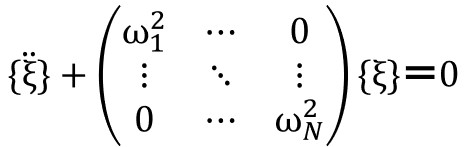
運動方程式はこのようになります。
この 運動方程式はN個独立した方程式が並んでいるだけなので、1次の固有振動数が知りたいだけなら、一番上の行の運動方程式を解けばよいわけです。
これまではN次の連立方程式を解いてN個の解を出す必要がありましたが、このように 座標変換をすることで計算がすごく楽になります。
まとめ
以上、長かったかもしれませんが、固有振動モードの計算の中身を示しました。
行列の扱いがたくさん出てきたので、線形代数が苦手な方は苦労するかもしれませんが、線形代数の勉強もしっかりして、理解を深めておきましょう。
参考文献
- 振動工学の基礎:岩壺卓三、松久寛、森北出版株式会社
- 機械力学-振動の基礎から制御まで:日高照晃、小田哲、川辺尚志、曽我部雄次、吉田和信、朝倉書店
- 構造と連続体の力学基礎:熊でもわかる変形できる物体の力学:岩熊哲夫、小山茂 web版
初心者向けの振動工学の教科書・参考書をこちらで紹介していますので、参考にしていただければと思います。
初心者向けの教科書・参考書はこちら
振動工学の記事一覧はこちら