単振動のときは複素数を使うメリットってあんまり感じなかったんだけど・・・


単振動のときは複素数を使うメリットってあんまり感じなかったんだけど・・・
本記事では複素数を使った、減衰のある強制振動の解法について説明します。
前回、単振動の運動方程式について、複素数を使って解説しました。
複素数を使うことで、計算量がグっと減ることを示していきますね。
本記事をおススメする人
- 複素数を使って減衰振動の運動方程式を解きたい人
- 物理を勉強していて興味がある人、仕事で振動の知識を使う人
動画でも解説していますのでこちらも是非参考にしてください。
減衰のある振動の運動方程式を解く
減衰のある強制振動の運動方程式
まず、減衰のある振動のモデルを先に示します。
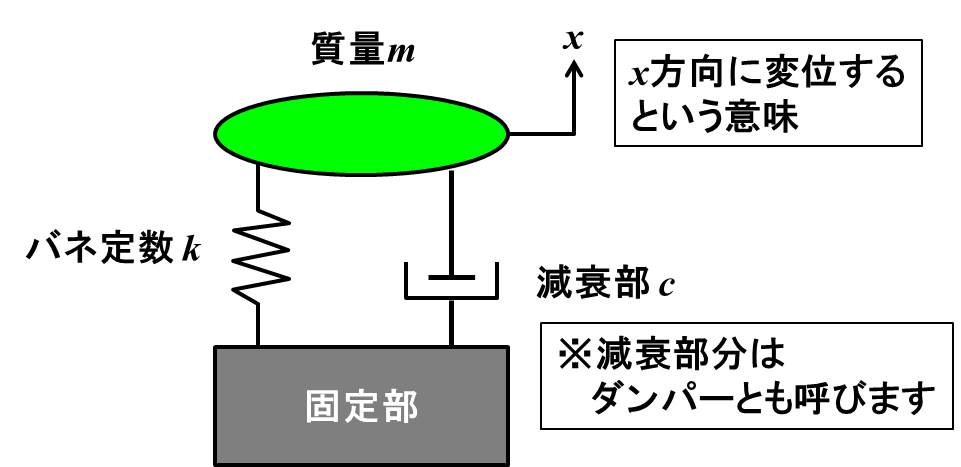
減衰は速度に比例する粘性減衰を仮定しています。
このモデルに強制振動するよう、質量の部分に周期的な外力を付け加えた運動方程式を考えます。
角振動数ωで周期的に変化する外力を、\(Fcosωt\)としますと、
複素数を導入して解く
外力のパターンとして、\(Fcosωt\)を仮定しましたが、\(Fsinωt\)のときも考えましょう。
この時の変位を\(x→y\)と書き換えると、運動方程式は、
$$m\ddot{y}+c\dot{y}+ky = Fsinω・・・②t$$
運動方程式②に虚数iをかけて、①との和をとると、
右辺は下記のオイラーの公式から、変形できます。
オイラーの公式
$$cosθ+isinθ=e^{iθ}$$
\(z=x+iy\)とすると、
③の式を見てみると、zを2回微分したものと、1回微分したものが含まれる微分方程式になっていますね。
この場合、eの指数関数で特殊解を設定すると、上手く計算できます。
特殊解を\(z=Ze^{iωt}\)とおくと、
\(e^{iωt}\)は両辺から消去できますので、Zの式に書き換えると、
$$Z=\frac{F}{-mω^2+k+icω}$$
となります。
Zは複素数を含んでいるので、複素振幅とも呼ばれますが、複素数を含んでいると、イメージがしづらくなります。
複素数の部分を分けるために、式変形を行いましょう。
分母の複素数の共役な複素数を、分母と分子にかけて、複素数成分を分子に持っていきましょう。
分子を三角関数の形(極座標の形)に変形することで、オイラーの公式を使えるようにできますので、書き換えましょう。
極座標のイメージは下記です。
虚部が負になっていますので、θが負になっていることに注意してください。
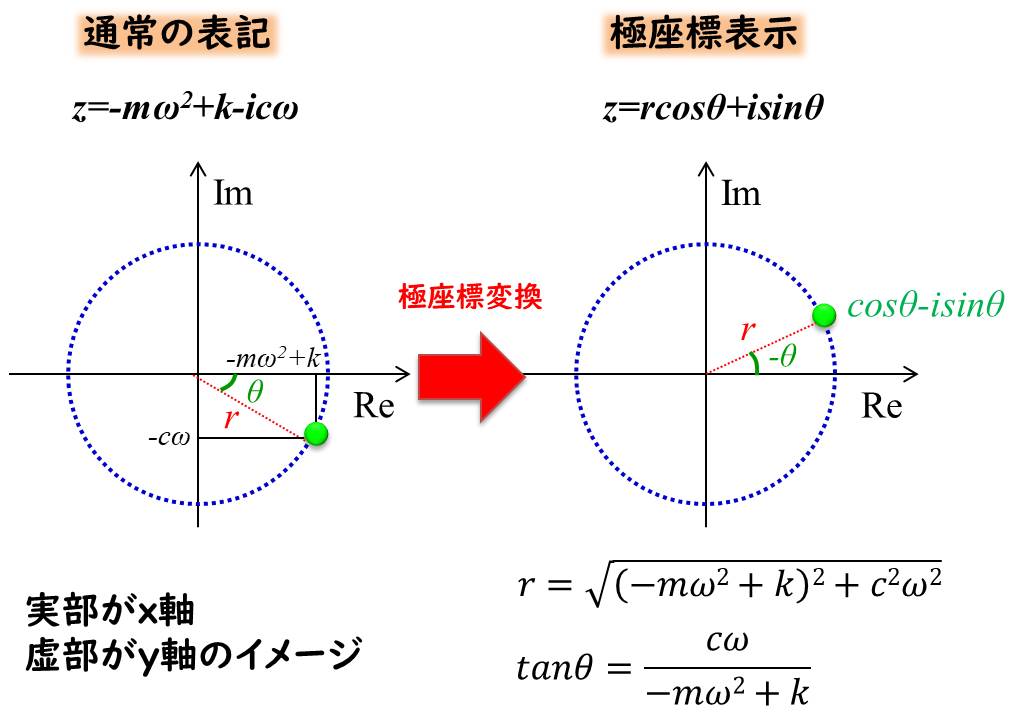
\(r\)は原点からの距離なので、三平方の定理から求まりますし、\(tanθ\)は傾きから求まりますね。
\(r=\sqrt{(-mω^2+k)^2+c^2ω^2}\)は④式の分母と約分できますので、
\(cosθ-isinθ=e^{-iθ}\)と置くと、
このように変形すると、\(e^{-iθ}\)以外は実数なので、係数部分を\(|Z|\)とすると、
$$Z=|Z|e^{-iθ}$$
となり、これを特殊解に代入すると、
$$z=|Z|e^{i(ωt-θ)}$$
三角関数の形で表記すると、
$$z=|Z|(cos(ωt-θ)+isin(ωt-θ))・・・⑤$$
よって、周期的外力を\(Fcosωt\)で与えた場合は、⑤式の実部が解となり、
\(Fsinωt\)で外力を与えた場合は⑤式の虚部が解となります。
複素数を使わない場合との比較
複素数を使わずに解く方法は過去の記事を参考にしてください。
こちらは動画でも解説していますので参考にしてください。
特殊解(特解)を求める際に、かなりの力業で、下記の連立方程式を解かなければいけません。
ここから、未知数\(A\)と\(B\)を求めるのですが、かなり手間です…
筆者も何回か計算ミスをしてしまいました。
複素数を使った方が、ミスなく、スマートに計算できますね。
まとめ
複素数を使用した場合、減衰ありの強制振動の解法がスマートであることを解説しました。
楽して計算したい方は、是非この計算方法を覚えておきましょう。
実際に、自由度が増えてくると、計算がものすごく複雑になるので、複素数を使わないと泣きをみることもあります。
高校数学の複素数や極座標の知識があれば、対応できますので、忘れた方は高校数学の復習をしながら勉強を進めましょう。
参考文献
- 振動工学の基礎:岩壺卓三、松久寛、森北出版株式会社
初心者向けの振動工学の教科書・参考書をこちらで紹介していますので、参考にしていただければと思います。
本サイトの振動工学のページはこちら。
初心者向けの教科書・参考書はこちら
振動工学の記事一覧はこちら
次の記事 → 振動・波動の基礎④-変位加振・地動加振・調和地動について 強制振動との違いも解説