なんで複素数を使って振動の運動方程式を解くの?


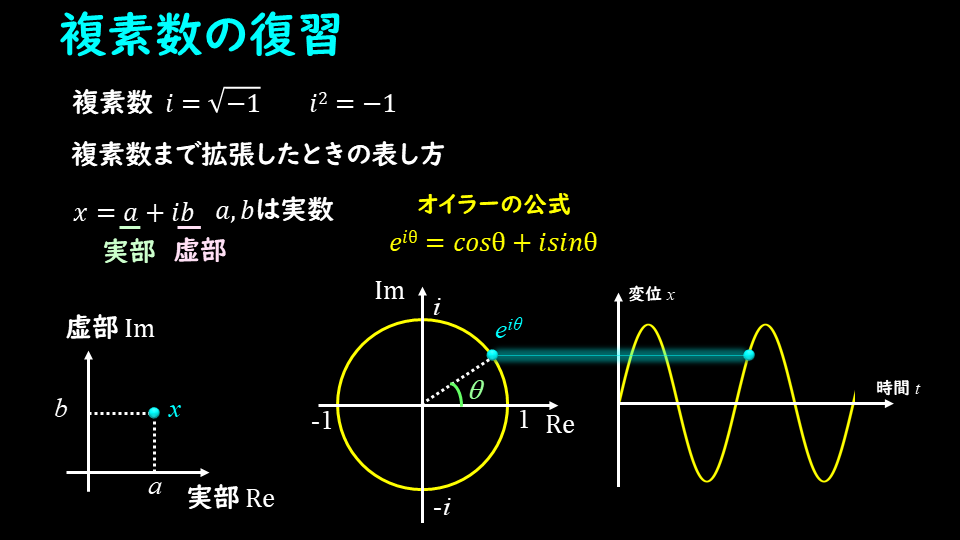
複素数を使うのは、計算が楽になるからなんだ。そもそも複素数も三角関数とよく似た部分があるので、まずは複素数の扱い方を、簡単な例で理解してみようね。
本記事では複素数を使った、運動方程式の解法について説明します。
まずは一番簡単な調和振動子で、その扱い方に慣れていきましょう。
そもそも調和振動や単振動って何?という方は過去の記事を参考にしてくださいね。
本記事をおススメする人
- 複素数を使った解法が理解できていない人
- 物理を勉強していて興味がある人、仕事で振動の知識を使う人
動画でも解説していますので参考にしてください。
調和振動子の復習

モデルと運動方程式
下記の図のような状態が調和振動子(単振動)のですね。
※物体と床の摩擦などは無視しています
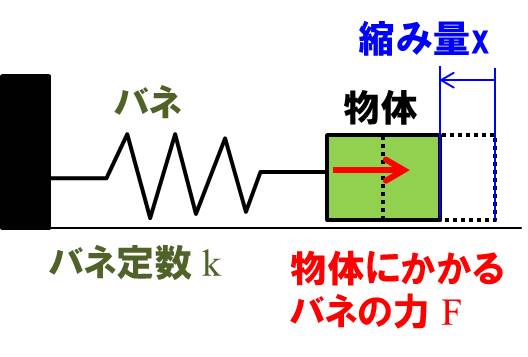
$$F=k×x$$
運動方程式は
$$m\ddot{x}=-kx$$
この微分方程式を解くと、変位の式は、
$$x = Asin(ωt+Φ)$$
結論として三角関数で示される、ということです。
複素数を用いた解法
では、複素数を使った解法に移ります。
単振動の運動方程式は、線形微分方程式であり、解き方として、特殊解を\(x=Ae^{λt}\)と置くパターンで解きます。
ここで、Aは実数ではなく、複素数もOKである複素解であることに注意してください。
このように置くと、運動方程式は、
\(Ae^λt\)を両辺から消去して、整理すると、
$$mλ^2+k=0$$
ここで両辺\(m\)で割って、\(ω=\sqrt{\frac{k}{m}}\)と置くと、
$$λ^2+ω^2=0$$
この式を特性方程式と呼びます。
さて、この特性方程式を満たすようなλは、どのような値になるでしょうか?
2乗して負の値にならなければいけませんので、複素数\(i\)を使用する必要があり、\(i\)を用いて解を表すと、
$$λ=±iω$$
λは+と-で2つ存在します。
それぞれ特殊解\(x=Ae^{λt}\)に代入すると、
線形微分方程式の一般解は、これら特殊解の線形結合で表されるので、一般解は、
となります。
三角関数への変形

一般解は求まりましたが、これは複素数を含むので、複素解と呼ばれます。
よく見る一般解の形にするために、オイラーの公式を使って三角関数へ変形します。
オイラーの公式は下記です。
$$e^{iθ}= cosθ+isinθ$$
この公式を用いると、一般解は、
実部と虚部で分けて整理しますと、
\(A_1\)と\(A_2\)は複素数なので、\(A_1=a_1+ib_1、A_2=a_2+ib_2\)とすると、
ここから、振動の状態を示す一般解を表すには、
- 実部、もしくは虚部の片方に注目する
- 実数になるように\(A_1、A_2\)を設定する
それではそれぞれの解法について解説しますね。
実部、虚部の片方に注目する

$$x=(a_1+a_2)cosωt-(b_1-b_2)sinωt+i\{(a_1-a_2)cosωt+(b_1+b_2)sinωt)\}$$
この式の実部、虚部の計算を行います。
まず実部を計算すると、
$$x=(a_1+a_2)cosωt-(b_1-b_2)sinωt$$
係数を下記のように置きます。
$$B_1=a_1+a_2、B_2=b_1-b_2$$
実部は下記のようになって、
$$x=B_1cosωt-B_2sinωt$$
三角関数の合成を行うと、
$$x=\sqrt{B_1^2+B_2^2}sin(ωt+φ_B)$$
ルートを\(B_0\)とおいて、
$$x=B_0sin(ωt+φ_B)$$
このように、単振動の一般解が導出されます。
一方、虚部も同様で、
$$x=(a_1-a_2)cosωt+(b_1+b_2)sinωt$$
係数を下記のように置きます。
$$C_1=a_1-a_2、C_2=b_1+b_2$$
実部は下記のようになって、
$$x=C_1cosωt+C_2sinωt$$
三角関数の合成を行うと、
$$x=\sqrt{C_1^2+C_2^2}sin(ωt+φ_C)$$
ルートを\(C_0\)とおいて、
$$x=C_0sin(ωt+φ_C)$$
こちらも単振動の一般解の形になりますね。
実数になるように$A_1,A_2$を決める
$$x=(A_1+A_2)cosωt+i(A_1-A_2)sinωt$$
この式の係数\(A_1+A_2\)と\(i(A_1-A_2)\)をそれぞれ\(C、D\)と置き、\(C、D\)が実数になるように\(A_1\)と\(A_2\)を設定します。
つまり
\(A_1\)と\(A_2\)は複素数なので、\(A_1=a_1+ib_1、A_2=a_2+ib_2\)とすると
②、③が実数になる条件は、\(b_1=-b_2\)、\(a_1=a_2\)となり、\(A_1\)と\(A_2\)が複素共役の場合、\(C、D\)は実数になりますね。
あとは\(x=Ccosωt+Dsinωt\)に対して、三角関数の合成公式を使用すると、
となり、複素数を用いても、三角関数の形の一般解となります。
なぜ複素数解法か?
いや、絶対に三角関数で解いた方が楽ですよ。


まぁ単振動の場合は三角関数で解いた方がスマートかもしれないね。でも減衰があったり、強制振動とか外力がある場合、複素数を使った方が、計算が楽になることが多いんだ。
今回は、単振動の式を無理やり複素数を用いて解いたので、少し複雑に感じたかもしれません。
しかし、 減衰があったり、強制振動の場合は複素数を用いた方が計算が少なくなりますので、複素数を用いる場合も多いです。
最終的に解が求まればよいので、三角関数でゴリゴリ計算できる方は不要かもしれませんが、計算ミスを嫌う方や、計算量を減らしたい方は便利な道具だと思って、複素数もマスターしておきましょう。
複素数の実部をとるイメージ
最後に、複素数の実部をとることで、振動の波形になることイメージしましょう。
下記のグラフはオイラーの公式で\(e^{iωt}=cosωt+isinωt\)としたときの、複素平面状の軌道と実部の動きを示しています。
横軸が実部(Re)、縦軸が虚部(Im)です。
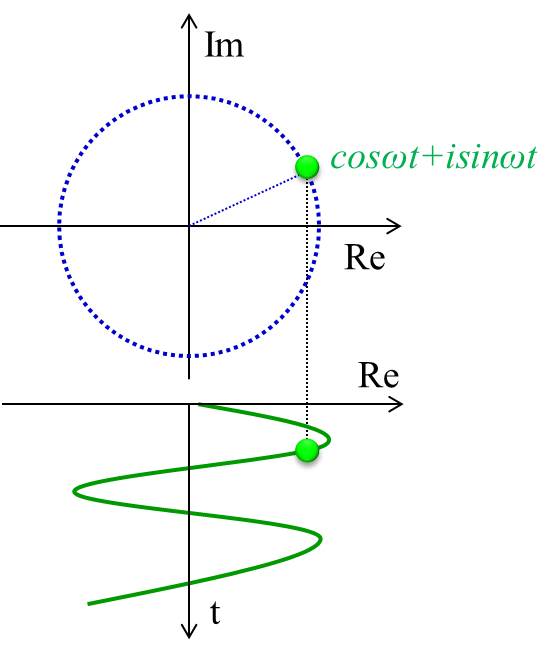
実部をとると\(cosωt\)で振動しているので、あとは初期位相と振幅次第で調和振動子の動きを再現できますね。
まとめ

本日は、複素数を用いて振動の運動方程式を解く、ということで、最も簡単な例である単振動の複素解法について解説しました。
今回は三角関数だけで解いた方が早いですが、次回以降、減衰を含む振動や強制振動での複素解法を紹介しますので、そこで有用性をしっかり理解していただければと思います。
初心者向けの振動工学の教科書・参考書をこちらで紹介していますので、参考にしていただければと思います。
初心者向けの教科書・参考書はこちら
振動工学の記事一覧はこちら
次の記事 → 振動・波動の複素解法 ②減衰無しの強制振動の運動方程式