圧力とかってどういうイメージを持てば良いの?


気体の分子運動から考えるとイメージしやすいので、気体分子運動論の説明をするね。
今回は圧力などの状態量についてイメージできるように解説します。
圧力とか温度とかのイメージができていると、熱力学の理解のしやすさが全然違いますので、しっかりと理解しておきましょう。
前回の記事で、熱力学の全体像を解説していますので、熱力学初心者の方は、まず全体像を把握してから勉強することをおすすめします。
また、本記事の内容は下記動画でも解説していますので、参考にしていただければと思います。
復習 熱力学の状態量
熱力学はたくさんの粒子をひとくくりにして、系として考える学問でした。
この系の状態を示すのが状態量で、高校物理の範囲では、下図のように圧力、温度、体積が大事でした。
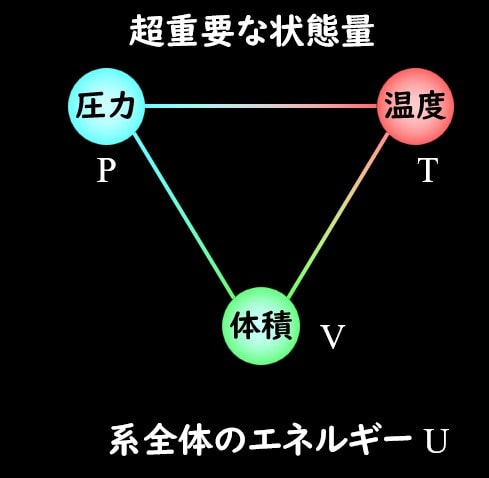
これら状態量は、理想気体の状態方程式に従うため、超重要だったわけですね。
また、上記3つの状態量に加えて、系の内部エネルギーUも重要な状態量です。
これは熱力学第一法則で表される状態量なので、非常に大事になっています。
それでは、圧力、温度、体積、内部エネルギーの4つのうち、まず圧力の説明をしますね。
圧力を気体分子運動論で考える
気体分子運動論で考えるってどういうこと?

これについては、気体粒子1つに着目して、運動を考えます。
その粒子が無数あったときに、平均を考えて、全体としてはどんな風に運動しているかを想像するような感じです。
イメージできない方も大丈夫、今は『ふ〜ん、そうなんだ』くらいでOKです。
1個の気体粒子に着目
まずは立方体の中にたくさんの粒子が入っているとします。
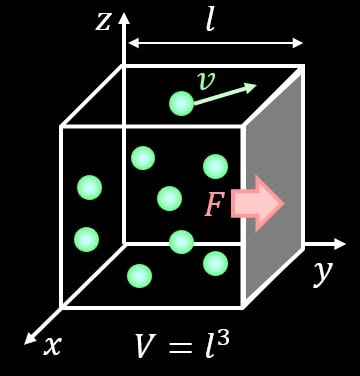
立方体の1つの面を取りだし、取り出した面にかかっている圧力\{P\}はどのように表されるかですが、面にかかっている力を\(F\)、面積を\(A\)とすると、
$$P=\frac{F}{A}$$
と表されますね。
\(A\)は指定した面の面積なので、すぐにわかる量になるのですが、力\(F\)がよくわからない量になります。
この力\(F\)を考えるのに気体分子運動論を取り入れて考えます。
それでは気体粒子1個に着目してみましょう。
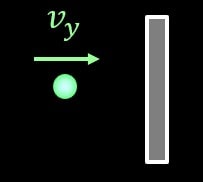
この気体粒子が速度\(v\)で等直線運動しているとします。
この粒子が\(y\)軸に垂直な壁にぶつかることを考えます。
壁に向かう速度は\(y\)軸方向の成分となるので、\(v_y\)となりますね。
圧力は壁に作用している力のようなものなので、壁に対して粒子が作用する力を考えます。
当然、壁と離れているときには壁に力を作用させることはできません。
粒子が壁にぶつかった時に初めて、壁に撃力として力を作用させることになりますね。
ここで、1つ大事な前提を入れます。
それは、気体粒子と壁の衝突は、『弾性衝突』であるということを前提とします。
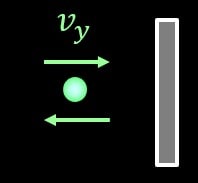
弾性衝突でなければ計算がややこしくなるので、この前提は必須です。
弾性衝突であれば、ぶつかった時の力積と運動量の関係は次のように表されます。
$$-fΔt=mv_y-mv_y$$
ここで、衝突したときの時間を\(Δt\)、質量を\(m\)としています。
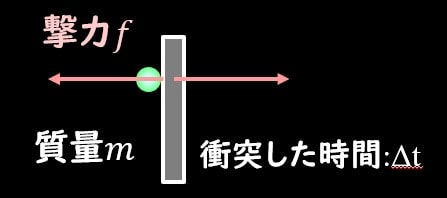
整理すると
$$fΔt=2mv_y$$
このように気体粒子が1回衝突すると、\(2mv_y\)の力積を生じることになります。
t秒間に何回衝突するか?
それでは、1個の粒子がt秒間に何回衝突するかを考え、力積がどのくらい発生するかを考えます。
立方体の1辺の長さは\(l\)なので、1往復の距離は\(2l\)となります。
1往復することで、考えている壁に1回衝突すると考えると、粒子は1秒間に\(v_y\)進むので、1秒間に衝突する回数は、\(\frac{v_y}{2l}\)回となりますね。
それでは\(t\)秒間に衝突する回数は
$$t×\frac{v_y}{2l}=\frac{v_yt}{2l}$$
となります。
つまり1個の粒子が\(t\)秒間に与える力積は
$$2mv_y×\frac{v_yt}{2l}=\frac{mv_y^2t}{l}$$
と計算することができます。
ここまでで、1個の粒子による力積が求まりましたので、次は粒子がたくさんあったときを考えましょう。
たくさんの粒子の力積を考える
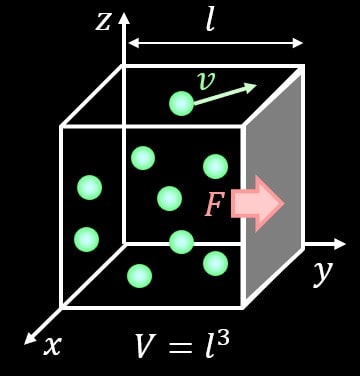
気体粒子がたくさんいるときを考えます。
ここまで、1個の粒子の\(y\)方向の速度を\(v_y\)としていましたが、たくさんの粒子の\(y\)方向の速度の平均を\(v_y\)とします。
(教科書とかでは\(<v_y>\)と書かれることもあります)
このようにすると、たくさんの粒子の数を\(N\)個とすると、\(N\)個の粒子が\(t\)秒間に与える力積は
$$\frac{Nmv_y^2t}{l}$$
と表すことができます。
このときの力積を\(F・t\)とすると
$$F・t=\frac{Nmv_y^2t}{l}$$
両辺の\(t\)を消去して、
$$F=\frac{Nmv_y^2}{l}$$
\(y\)方向の速度を使って力積を表すと、このようになります。
しかし\(v_y\)って勝手に設定した速度なので、もっと一般的なたくさんの粒子の速度平均\(v\)を使って表すことを考えます。
どのように式変形するかといいますと、速度の等方性から下記のような関係式を使うことができます。
$$v_x^2=v_y^2=v_z^2$$
めちゃくちゃたくさんの粒子があると、\(x\)方向の速度も\(y\)方向の速度も\(z\)方向の速度も平均的には一緒になりますよ、という式です。
また、\(N\)個の粒子の速度平均\(v\)については
$$v^2=v_x^2+v_y^2+v_z^2$$
という風に書くこともできますので、等方性の式と合わせると、
$$v_y^2=\frac{v^2}{3}$$
という式を得ることができますね。
この式を力積の式に代入すると、
$$F=\frac{Nmv^2}{3l}$$
このように力積の関係から、力\(F\)を求めることができました。
力\(F\)がわかれば、圧力\(P\)は力\(F\)を面積\(A\)で割ってあげればよいので、
$$P=\frac{F}{A}=\frac{F}{l^2}=\frac{Nmv^2}{3l^3}$$
分母の\(l^3\)は体積\(V\)と等しいので、
$$P=\frac{Nmv^2}{3V}$$
となります。
圧力は粒子の質量、速度、粒子数が大きいと大きくなるのはイメージ通りではないでしょうか?
言い換えると、圧力は壁が無数の粒子にどつかれた度合、とも言えますね。
まとめ
状態量のうち、気体の圧力について、分子運動論の観点から解説しました。
分子運動論は1つの粒子の運動を考えて、それを無数の粒子の運動へ拡張させて考える手法でした。
この手法で圧力を考えると、圧力は壁が無数の粒子にどつかれた度合、というイメージになって、下記のような式で表すことができます。、
$$P=\frac{Nmv^2}{3V}$$
式自体を覚える必要はありませんが、しっかりと圧力を頭でイメージできるようにしておきましょう。
