ねじれモーメントってどうやって求めたらいいの?


ねじれモーメントはせん断力によるモーメントの総和になるよ。
本記事ではねじれモーメントの求め方と、物体のねじれにくさを示す断面2次極モーメントについて解説します。
よく似たねじれにくさを示す指標として、ねじり剛性という単語もありますが、そちらとの違いについても解説しますね。
過去の記事でねじれの変形時にはせん断力が発生することを解説していますので、参考にしていただければと思います。
また、動画でも解説していますので、参考していただければと思います。
モデル
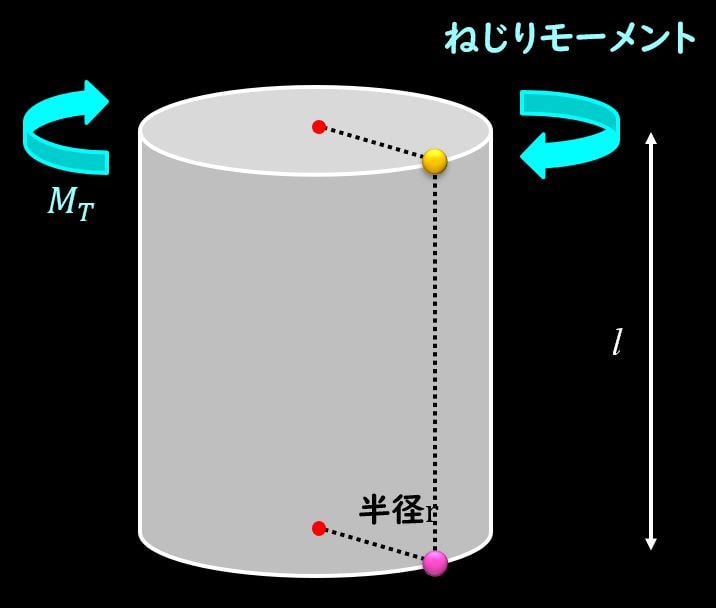
今回は上図のように円柱がねじれる場合を考えます。
円柱の半径を\(r\)、高さを\(l\)とし、ねじりモーメント\(M_t\)でねじったような状態です。
復習 ねじれによるせん断力
過去の記事で解説した通り、ねじれた際の青の面の変形を考えると、せん断力が生まれることがわかります。
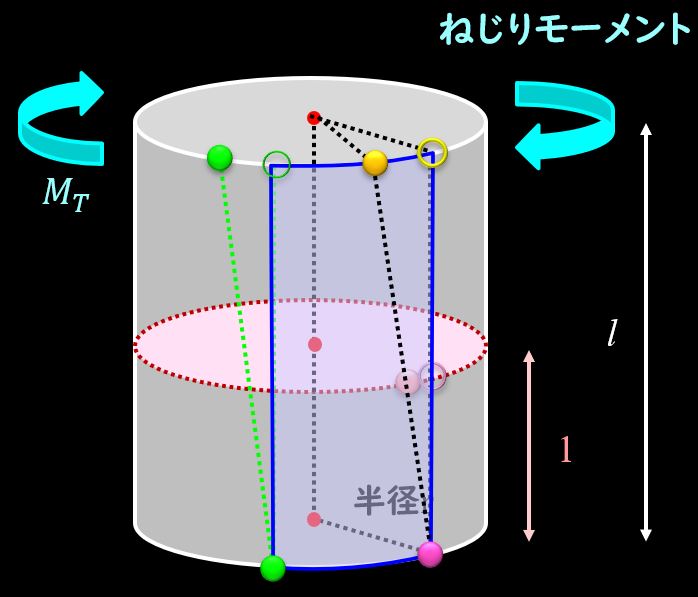
せん断力は、横弾性係数を\(G\)、比ねじれ角を\(θ\)、円柱の半径を\(r\)とすると、下記のようになります。
$$τ=Grθ\tag1$$
これはせん断ひずみ\(γ\)が微小角なので、
$$tanγ≒γ\tag2$$
となり、さらに\(tanγ\)は図形的に、
$$tanγ=\frac{rφ}{l}\tag3$$
となります。ここで\(φ\)は高さ\(l\)の面における、ねじれ角です。
ねじれ角\(φ\)と比ねじれ角\(θ\)との関係は、
$$θ=\frac{φ}{l}\tag4$$
となるので、(4)式を(1)式に代入することで、せん断力が求まりますね。
ねじれモーメントを導出
さて、ここまでだと、ねじれモーメントとせん断力が結びついていないので、
どれくらいのモーメントが作用したら、どれくらいのせん断力が発生するのか、がわからない状態です。
ということで、ねじれモーメントとせん断力の関係性を理解しておく必要があるわけですが、
結論的にはねじれモーメントは、せん断力によって発生するモーメントをたし合わせたもの、となっております。
考えている面全体でのモーメントを足し合わせる必要があるので、積分をする必要があります。
それでは実際に積分をしてみましょう。
積分の考え方については、微小領域に発生するモーメントを考え、積分によって足し合わせる、という流れで行います。
まず微小領域に発生するモーメントですが、下図のピンクの微小領域のように、中心からの距離\(r’\)の微小面積を考えます。
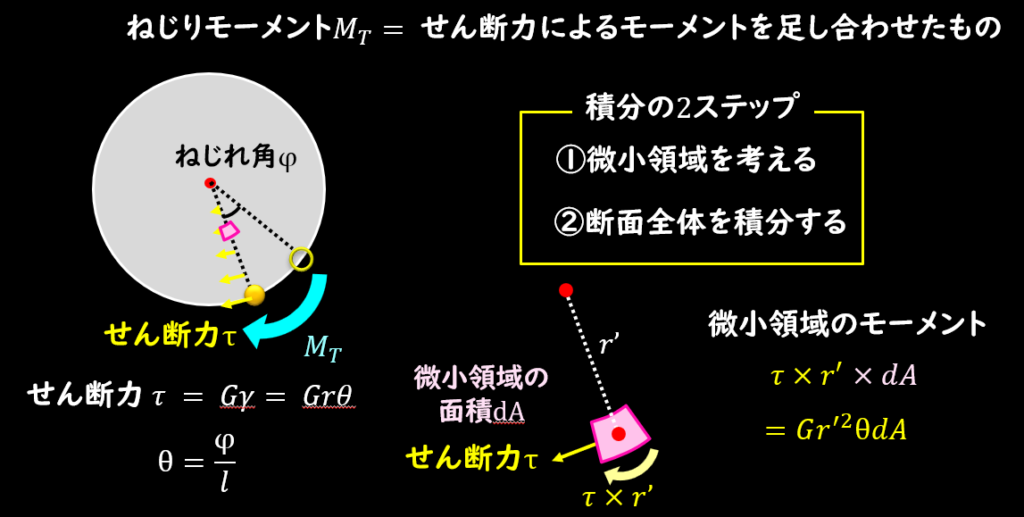
この距離r’の点におけるせん断力は、
$$τ=Gr’θ\tag5$$
ですね。
この点におけるモーメントは距離をかけることで\(Gr’^2θ\)と求まります。
この点に微小面積\(dA\)を作ってあげて、微小面積に発生しているモーメントは\(dA\)をかけることでもとまるので、
$$Gr’^2θ×dA\tag6$$
となります。
ここまでで、微小領域に発生するモーメントが求まりましたので、積分しましょう。
$$\int{Gr’^2θdA} \tag7$$
微小面積\(dA\)については、極座標系で、次の形で表すことができます。
$$dA=rdrdθ\tag8$$
この(8)式を(7)式の積分へ代入すると
$$\int Gr’^2θr’dr’dθ=\int Gr’^3θdr’dθ\tag9$$
このように求まります。
この積分を実行することで、ねじれモーメントを求めることができます。
断面2次極モーメント
先ほどの積分の式を見てみましょう。
$$M_T=\int{Gr’^2θdA}\tag{10}$$
この式で\(G\)、\(θ\)を積分の外に出してみると、
$$M_T=Gθ\int{r’^2dA}\tag{11}$$
このように書けます。この(11)式における積分の部分のことを断面2次極モーメントと呼んでいます。
断面2次極モーメントは
$$I_P=\int r’^2dA\tag{12}$$
となりますね。
で、これが何を意味しているの?


断面2次極モーメントは構造的なねじれにくさを示しているんだよ。
断面2次極モーメントを使うと、ねじれモーメントは下記のように表すことができますね。
$$M_T=GI_Pθ\tag{13}$$
この(13)式の中の\(G×I_P\)の部分はねじれ剛性と呼んでおり、その物体がどれだけねじれにくいかを示しています。
その中で\(I_P\)は構造的なねじれにくさを示しており、
\(Gは\)横弾性係数で材料で決まる係数ですので、材料によるねじれにくさを示してます。
もう少し噛み砕いて説明すると、断面2次極モーメント\(I_P\)は、その物体の形状、円柱なのか、四角柱なのか、球なのか・・・
そういった構造で決まるパラメータです。
一方、横弾性係数\(G\)は材料によって決まるパラメータですので、例えば、鉄でできているとか、プラスチックでできているとか、ゴムでできているとか・・・
そういった材質によって決まるねじれにくさを示しているわけです。
ねじれ剛性は断面2次極モーメントと横弾性係数の掛け算なので、構造とか材質とかひっくるめてどれくらいねじれにくいか、を表しています。
具体的に断面2次極モーメントを計算してみる
それでは実際に今回取り扱ったモデルの計算をしてみましょう。
$$M_T=\int^{2π}_0\int^r_0 Gr’^3θdr’dθ’\tag{14}$$
この二重積分を実行すればよいわけなので、積分しましょう。
まず、積分の中に変数\(θ’\)は存在しないので、\(θ’\)に関する積分は\(2π\)となります。
\(r’\)に関する積分を実行すればよく、
$$M_T=2πGθ\left[\frac{1}{4}r’^4\right]^r_0\tag{15}$$
これを計算すると、
$$M_T=\frac{πGr^4θ}{2}\tag{16}$$
この\(\frac{πr^4}{2}\)の部分が断面2次極モーメントを示しており、円柱の半径によって決まることがわかりますね。
つまり、断面2次極モーメントは構造によって定まるパラメータということになります。
なお、通常この断面2次極モーメントの計算は実施する必要はなく、便覧等で調べて使っていくことがほとんどだと思います。
まとめ
ねじれモーメントの導出と、断面2次極モーメントについて解説しました。
ねじれモーメントは、ねじりによって生じたせん断力によるモーメントを足し合わせることで、求めることができるのでした。
断面2次極モーメントは、構造的なねじれにくさを示しているパラメータで、
横弾性係数との掛け算した$GI_P$がねじれ剛性と呼ばれるもので、材料や構造に関係なく、どれくらいねじれにくいのかを示していました。
一方、横弾性係数は材料的なねじれにくさを示しているのでしたね。
このあたりの用語とイメージをしっかりともつことができることが大切です。
初心者向けの教科書・参考書はこちら
材料力学の記事一覧はこちら
