連続体の横振動の運動方程式って解けるの?


弦の振動や縦振動と運動方程式は異なるけど、ちゃんと解けるので横振動について運動方程式を解いてみよう。
今日は梁の横振動の自由振動について解説します。
横振動の運動方程式については過去の記事で解説していますので、参考にしてください。
ポイント
動画でも解説していますので、参考にしていただければと思います。
モデルと運動方程式
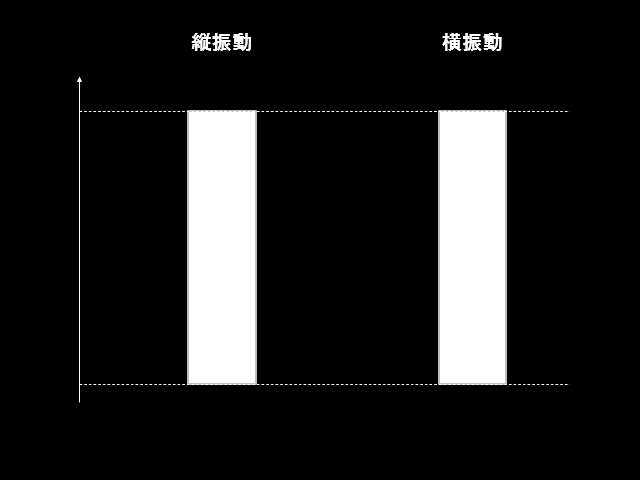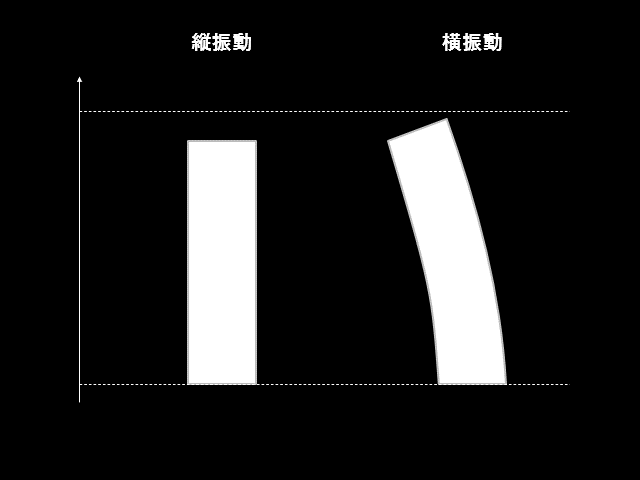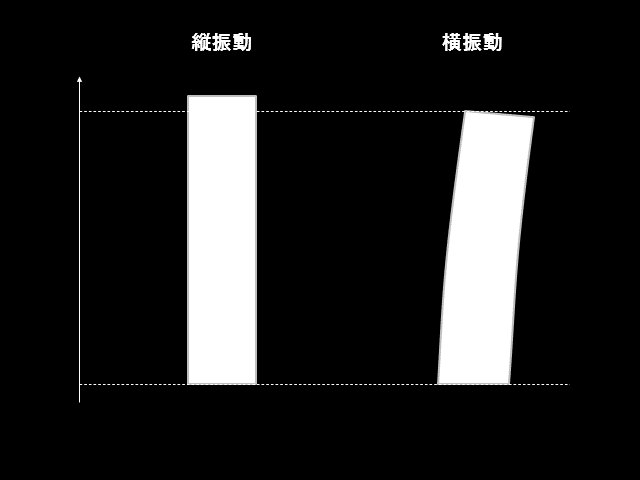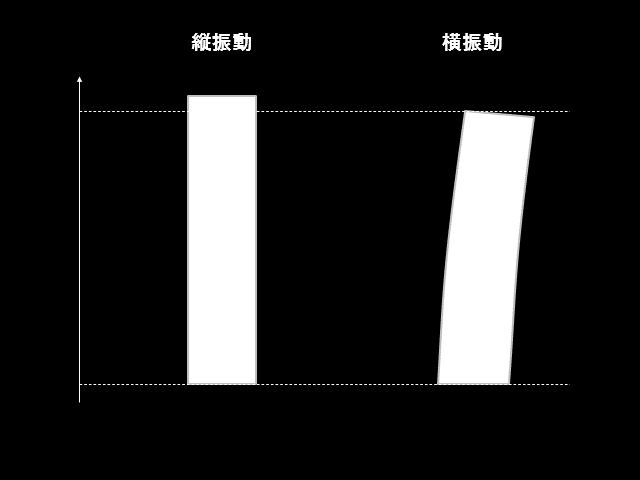
まず横振動と縦振動の違いについては上図のように、振動する方向が違うことに注意しましょう。
詳細はこちらの記事で解説していますので、参考にしてください。
モデル
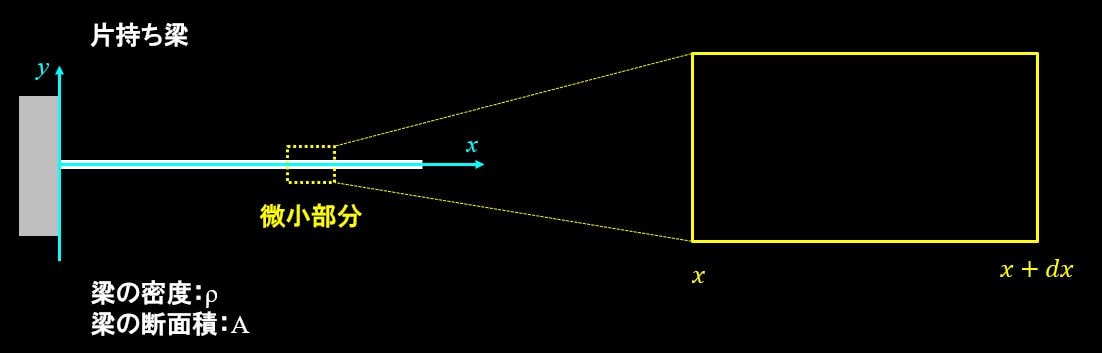
上図のような片持ち梁を考えましょう。
このような片持ち梁の微小部分を考えて、微小部分について\(x\)軸、\(y\)軸をとると、 \(y\)方向の運動方程式は、下記のようになります。
$$ρA\frac{\partial^2 y(x,t)}{\partial t^2}+\frac{\partial^4y }{\partial x^4}=0$$
\(ρ\)は梁の密度、\(A\)は梁の断面積、\(E\)はヤング率、\(I\)は断面二次モーメントです。
運動方程式を解く
運動方程式は4階の偏微分方程式になっているので、下記のように解を仮定して変数分離法で解きます。
$$y(x,t)=Y(x)G(t)$$
これを運動方程式に代入すると、
$$ρA\frac{\partial^2 }{\partial t^2}Y(x)G(t)+\frac{\partial^4}{\partial x^4}Y(x)G(t)=0$$
左辺の\(t\)の偏微分の外に\(Y(x)\)は出すことができ、\(x\)の偏微分の外に\(G(t)\)を出すことができるので、
$$ρAY(x)\frac{\partial^2 }{\partial t^2}G(t)+G(t)\frac{\partial^4}{\partial x^4}G(t)=0$$
左辺に\(x\)の関数、右辺に\(t\)の関数が来るように式を整理すると、
$$\frac{EI}{ρAY(x)}\frac{d^4}{dx^4}Y(x)=-\frac{1}{G(t)}\frac{d^2}{dt^2}G(t)$$
このように式を整理すると、左辺=右辺となるためには、左辺も右辺も一定値とならなければならないので、その定数を\(ω^2\)と置くと、
$$\frac{EI}{ρAY(x)}\frac{d^4}{dx^4}Y(x)=ω^2$$ $$-\frac{1}{G(t)}\frac{\partial^2 G}{\partial t^2}=ω^2$$
となります。
\(x\)の式を変形すると、
$$\frac{d^4Y}{dx^4}-\frac{ρA}{EI}ω^2Y(x)=0$$
ここで、\(Y\)の係数を下記のようにkを使って表します。
$$k^4=\frac{ρA}{EI}ω^2$$
このようにすると、
$$\frac{d^4Y}{dx^4}-k^4Y(x)=0$$
続いて、\(G(t)\)についての式を整理しますと、
$$\frac{d^2G(t)}{dt^2}+ω^2G(t)=0$$
このように、位置の関数と時間の関数の微分方程式を得ることができます。
位置の関数\(Y(x)\)を解く
\(Y(x)\)は4階同次線形微分方程式となっていますが、解き方としては、基本解を4つ見つけて、基本解を線形結合するという形になります。
基本解は1次独立な特殊解、と考えていただいて大丈夫です。
つまりそれぞれが定数倍で表すことができない解、それが基本解ですね。
微分方程式の特殊解を\(e^{λx}\)と置いて、微分方程式に代入すると、
$$λ^4e^{λx}-k^4e^{λx}=0$$
両辺を\(e^{λx}\)で割ると、
$$λ^4-k^4=0$$ $$(λ^2-k^2)(λ^2+k^2)=0$$
\(λ=±k,±ik\)がこの式の解となります。
それぞれを代入したものは、1次独立の関係にあるので、4つの解を特殊解へ代入したものを基本解として、線形結合すると、
$$Y=Y_1e^{kx}+Y_2e^{-kx}+Y_3e^{ikx}+Y_4e^{-ikx}$$
これらは双曲線関数と三角関数を用いて表すことができて、
$$Y=C_1sinhkx+C_2coshkx+C_3sinkx+C_4coskx$$
このように\(Y(x)\)の一般解が求まりました。\(C_1~C_4\)は未定定数です。
時間の関数\(G(t)\)を解く
$$\frac{d^2G(t)}{dt^2}+ω^2G(t)=0$$
この式は単振動の運動方程式と同じ形なので、一般解は下記のように表すことができます。
$$G(t)=Acosωt+Bsinωt=A_0sin(ωt+Φ)$$
単振動の運動方程式の解き方がわからない方はこちらの記事を参考にしてください。
以上のように、梁の一般解が求まり、未定係数\(C_1~C_4\)と\(A,B\)については、初期条件や境界条件によって決まります。
梁の横振動の場合、梁の端部の固定の仕方で、初期条件が決まりますので、具体的な固定と境界条件については次回以降に解説します。
まとめ
今回は梁の横振動について、運動方程式を解いて一般解を導出しました。
一般解の形は双曲線関数と三角関数の和で表されることになり、未定係数については、梁の固定の仕方によって変わります。
梁の固定の仕方については次回以降で解説しますので、次回を楽しみにしておいてください。
参考文献
- 振動工学の基礎:岩壺卓三、松久寛、森北出版株式会社
- 機械力学-振動の基礎から制御まで:日高照晃、小田哲、川辺尚志、曽我部雄次、吉田和信、朝倉書店
- 構造と連続体の力学基礎:熊でもわかる変形できる物体の力学:岩熊哲夫、小山茂 web版
初心者向けの教科書・参考書はこちら
振動工学の記事一覧はこちら
次の記事 → to be continued
