連続体の振動って自由振動の解ってどうなるの?


それじゃあ今日は自由振動の解を求めてみよう。
今回は両端固定の弦についての自由振動の一般解について解説します。
前回の運動方程式(波動方程式)を使えばすぐに簡単にでてきますので、サクッと導出しましょう。
モデル 詳細は過去の記事を参考にしてください。
運動方程式
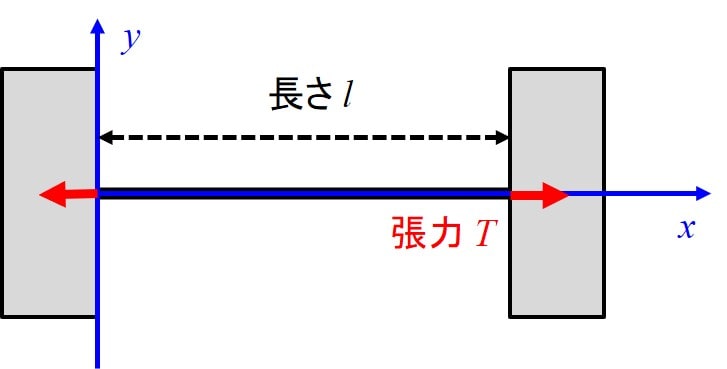
運動方程式は下記のようになります。
$$\frac{\partial^2y}{\partial t^2}=c^2\frac{\partial^2y}{\partial x^2}$$
この\(y(x,t)\)はたわみ量を示していて、\(x\)と\()t\)の関数で表されます。
この\(y\)を\(x\)の関数とtの関数の積で表せるとして、変数分離法で分離しますと、 $$y(x,t)=Y(x)G(t)$$ という形になります。
運動方程式を解く
運動方程式を解くには、下記のように解を仮定します。
『弦の各微小な部分は、時間的に正弦波(三角関数)状に振動する』 この仮定を反映させるために、下記のように\(G(t)\)を仮定します。
$$G(t)=e^{iωt}$$
このようにすると、変数分離した解は、
$$y(x,t)=Y(x)G(t)=Y(x)e^{iωt}$$
この式を運動方程式に代入すると、
$$-ω^2Y(x)e^{iωt}=c^2\frac{\partial^2Y(x)}{\partial x^2}e^{iωt}$$
式を整理すると
$$\frac{\partial^2Y(x)}{\partial x^2}+\frac{ω^2}{c^2}Y(x)=0$$
この微分方程式は単振動の運動方程式と同じ形ですね。
(厳密には通常の単振動の運動方程式は時間についての微分方程式ですが、 今回は\(x\)についての微分方程式なので異なります)
一般解
一般解を求めると、
$$Y(x)=Asin\frac{ωx}{c}+Bcos\frac{ωx}{c}$$
今回、両端固定の弦なので、\(Y(0)=Y(l)=0\)という境界条件が成り立ちます。
これらを代入すると、
$$Y(0)=B=0$$
$$Y(l)=Asin\frac{ωl}{c}+Bcos\frac{ωl}{c}=Asin\frac{ωl}{c}=0$$
A=0としてしまうと、弦が振動していないことになってしまいますので、 A≠0となり、
$$sin\frac{ωl}{c}=0$$
となります。
よって、
$$ω_n=\frac{nπc}{l}$$
このように\(n\)個の解が基本解(互いに1次独立の解)が求まります。 ちなみにn=1,2,3,…なので、無限個の基本解が存在します。
微分方程式の解は、基本解の線形結合で表すことができるので、まずn番目の基本解\(y_n\)を書くと、
$$y_n(x,t)=Y(x)e^{iω_nt}=A_ne^{iω_nt}sin\frac{ω_nx}{c}=A_ne^{iω_nt}sin\frac{nπx}{l}$$
\(A_n\)は任意定数で、\(n\)番目の振動モードの振幅を示します。
一般解は無数に存在する基本解の線形結合なので、下記のようになります。
$$y(x,t)=\sum_{n=1}^{\infty}y_n(x,t)=\sum_{n=1}^{\infty}A_ne^{iω_nt}sin\frac{nπx}{l}$$
以上が両端固定の弦の一般解です。
このように 各固有振動モードの波を足し合わせることで、一般解は書くことができます。
これは多自由度の振動系と同じですね。
振動・波動の基礎-㉒モード合成について 固有振動モードを重ね合わせる!
まとめ
本日は連続体として両端固定の弦について、自由振動の一般解を計算しました。
抑えておくポイントとしては、『 自由振動は各固有振動の和(重ね合わせ)で表すことができる』という点です。
これは微分方程式の解法から来ている面がありますが、多自由度系でも同じ考え方なので、覚えておきましょう。
次回は具体的に初期条件を決めて、一般解の形を導出します。
振動・波動の基礎-㉕連続体の振動 両端固定の弦の自由振動一般解の具体例をわかりやすく解説
参考文献
- 振動工学の基礎:岩壺卓三、松久寛、森北出版株式会社
- 機械力学-振動の基礎から制御まで:日高照晃、小田哲、川辺尚志、曽我部雄次、吉田和信、朝倉書店
- 構造と連続体の力学基礎:熊でもわかる変形できる物体の力学:岩熊哲夫、小山茂 web版
初心者向けの振動工学の教科書・参考書をこちらで紹介していますので、参考にしていただければと思います。
初心者向けの教科書・参考書はこちら
振動工学の記事一覧はこちら
次の記事 → 振動・波動の基礎-㉕連続体の振動 両端固定の弦の自由振動一般解の具体例をわかりやすく解説
