状態方程式っていったい何なの?

理想気体の状態方程式は非常に重要な式なので、しっかりと覚えておきましょう。
今回は理想気体の状態方程式について解説します。
高校物理や化学でも習いますが、形としては下記のように表されます。
$$PV=nRT\tag1$$
この式と密接に関係があるボイルの法則、シャルルの法則についても説明しておきます。
熱力学の状態量
前回までの記事で、状態方程式の中の状態量について解説していますので、詳細はそちらもぜひ参考にしていただければと思います。
【初心者向け】熱力学の考え方と全体像を解説 エネルギー保存と状態量
【初心者向け】熱力学 圧力をイメージする!気体分子運動論で考える
【初心者向け】熱力学 温度のイメージを気体の分子運動論で考える
熱力学で重要な状態量として、下記のように示していました。
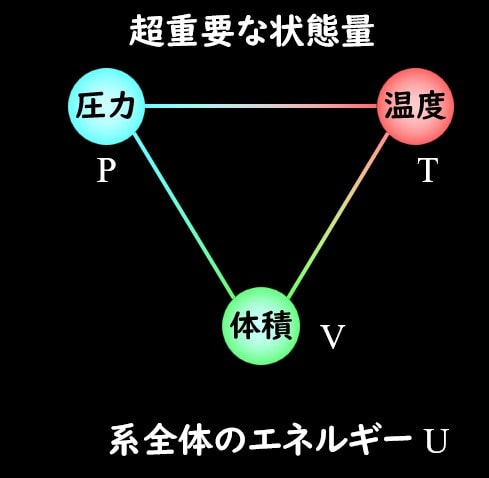
圧力\(P\)、体積\(V\)、温度\(T\)、内部エネルギー\(U\)が高校物理でも習うパラメータですね。
これらは系の状態を表すパラメータであって、非常に重要です。
これらの状態量を結びつけるのが状態方程式であったり、ボイルの法則、シャルルの法則なので、そちらの解説に移りましょう。
理想気体の状態方程式
冒頭でも出てきた通り、状態方程式は下記のように表すことができます。
$$PV=nRT\tag1$$
\(n\)は気体のモル数、\(R\)は気体定数で、このように状態量がつながっております。
注意点としては、この状態方程式が成り立つのは理想気体の単原子分子のときに限ります。
理想気体とは気体粒子同士の分子間力を無視した気体となっています。
当然、粒子間には分子間力が働くので、実際には存在しない気体なのですが、
分子間力を考えると計算が難しくなることも多いので、理想気体の状態方程式を使うことが多いわけなんです。
もう一つ、単原子気体については、水素分子とかのように水素原子が2つくっついた気体ではなく、
ハロゲンのArとかXeとか、原子が1つだけで気体として存在してる気体をイメージしていただければと思います。
これらがずれると状態方程式から式がずれますので、注意しておきましょう。
ボイルの法則、シャルルの法則
さて、次にボイルの法則、シャルルの法則についてですが、これらは状態方程式ができる前に発見された法則で、
意味している内容は状態方程式に含まれるような形になっていますので、覚える必要性は低いです。
ですが、解説しないというのはさすがにボイルさんとシャルルさんに失礼ですので、解説しますね。
その上で覚えるかどうかを考えていただければと思います。
ボイルの法則
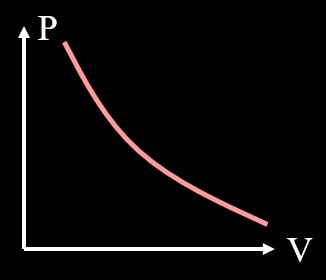
ボイルの法則は、温度が一定の場合、圧力と体積の積が一定となる法則です。
$$PV=const.\tag2$$
これは状態方程式を考えてみると、右辺が全て定数となることからも理解できますね。
グラフを書くと下図のようになります。
シャルルの法則
圧力が一定の場合、体積と温度は比例する、という法則です。
$$V∝T\tag3$$
これも状態方程式を変形して、
$$V=\frac{nRT}{P}\tag4$$
となって、右辺は\(T\)以外が定数となるので、シャルルの法則と同じ意味となるわけです。
グラフで書くと下記のようになりますね。
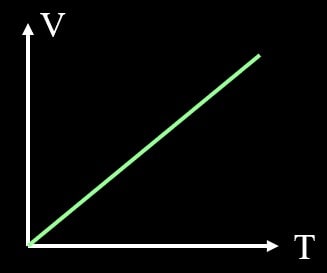
まとめ
以上、高校物理でも習う理想気体の状態方程式を復習しました。
ボイルの法則、シャルルの法則と状態方程式の関係性についても解説しました。
状態方程式をしっかりと理解しておけばこれらの法則に頼ることもないことが理解できたのでは無いでしょうか?
