なんか移動してる物体の中の流体の問題が出てきてよくわからないんだけど…


流体自体は止まっているとみなすこともできるので、今までの知識で解けるよ。がんばろー。
今回から2回の講義で、動いている物体の中の流体について解説します。
液体の入った容器を運搬したり、洗濯機の渦だったりを取り扱います。
新たに考えるのは慣性力です。
高校物理でも習った内容ですね。
この記事では、流体が相対的に静止している状態を扱います。
流体が静止していない状態はなかなかややこしいので、流体が止まっている状態を考えましょう。
動画での解説はこちらです。
慣性力は見かけの力
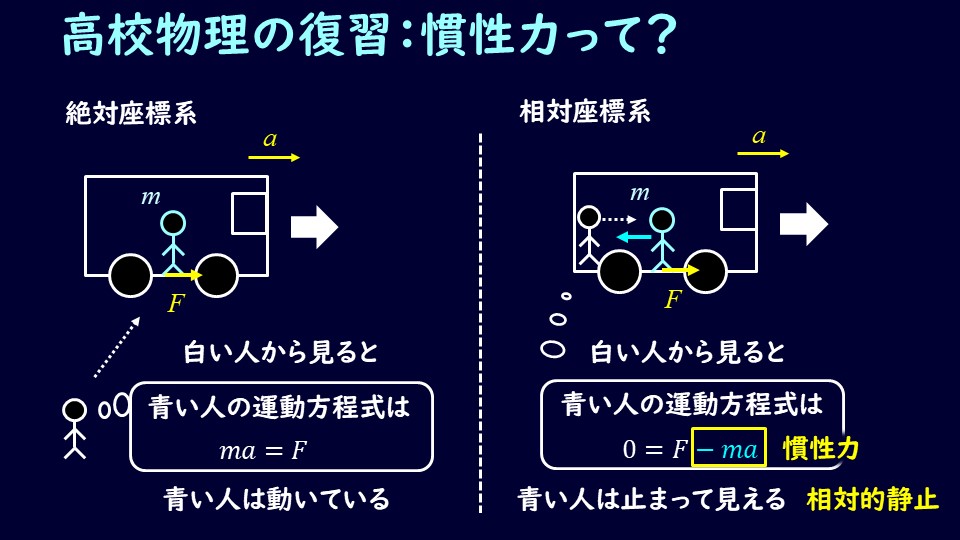
電車の中でおっとっと、となったことがある人はたくさんいると思います。
電車の外から見ると、電車の中にいる人は電車の床から摩擦を受けて移動している、とみなすことができますね。
これを電車の中から見ると、電車や中の人は止まっているように見えます。
止まっているように見えるのに、何かの力が働いておっとっと、となっているわけですね。
この『何かの力』が『慣性力』に相当します。
何かしら加速度が発生しているような乗り物に乗っていると、乗り物に乗っている人から見ると慣性力が働いているように見える、ということです。
大事なのは加速度であって、等速直線運動しているような状態では慣性力は発生しません。
同じスピードで走っている車や電車の中にいても、おっとっと、という風にはなりませんよね?
慣性力が働いている状態での液面
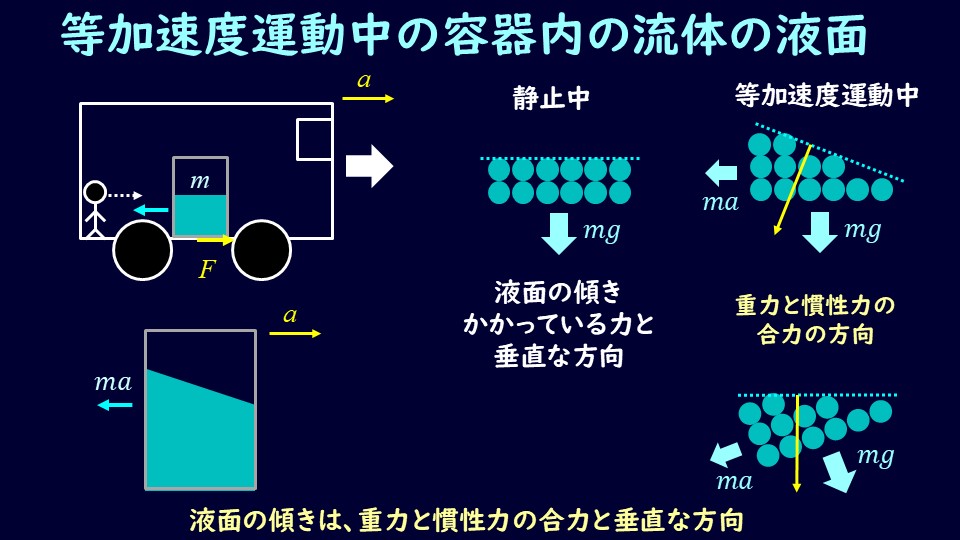
さて、慣性力が働いている場合の液面について考えましょう。
水を入れたコップを持って、急発進、急ブレーキをかけると、水はこぼれますね。
これは慣性によって液面が水平ではなくなるからですね。
このイメージを忘れずに、等加速度運動している状態を考えましょう。
等加速度運動している乗り物に乗り、乗り物の中で持っている容器に水を入れます。
そうすると乗り物に乗っている人から容器の液面を見ると、徐々に液面が傾き、傾いた状態で液面が静止していきます。
この静止している状態を相対的な静止と呼びます。
相対的、という名前になっているのは、乗り物の外からみると液体は乗り物と一緒に移動しているように見えるからですね。
さて、この相対的な静止の状態における力の状態を考えてみましょう。
液体にかかっている力は2つ、重力と慣性力ですね。
重力は液体の質量を\(m\)、重力加速度を\(g\)とすると\(mg\)ですね。
慣性力は先ほど説明したとおり、加速度を\(a\)とすると\(ma\)となります。
これら2つを合わせると、液体にはこのような合力が発生することになります。
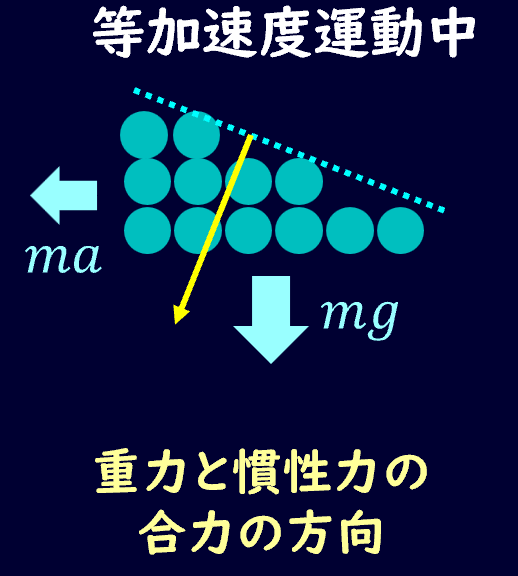
さて、液体に斜めに合力がかかると液面はどうなるでしょうか?
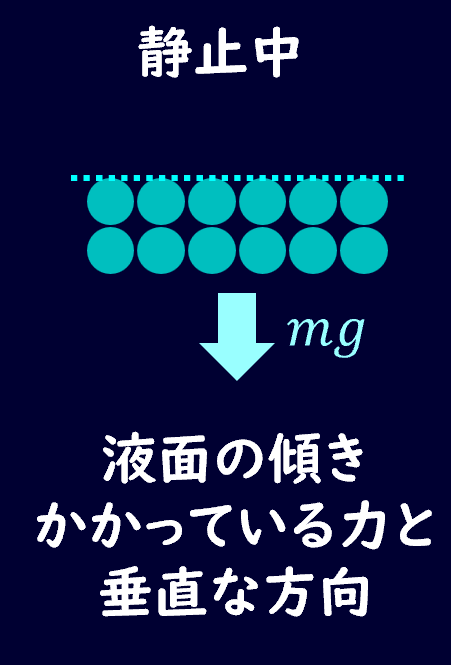
真下に重力のみがかかっている場合は、液面は水平になりますね。
つまり、液面は力がかかっている方向に対して垂直になります。
なので斜めに合力がかかっている場合も同様に考えて、液面は合力に対して垂直になります。
合力に対して垂直になっていないと、流体をコロコロ動く粒子の集合とみなした時、流体が合力に対して垂直方向にコロコロ転がってしまいますね。
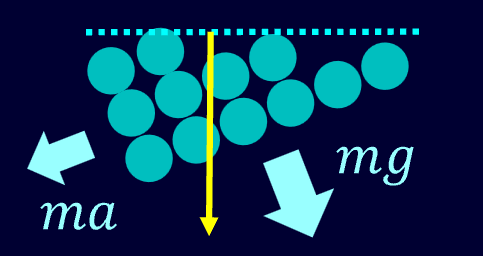
最終的には合力に対して垂直になることで、液面が移動しなくなる、ということになります。
流体内の圧力

液面が重力と慣性力の合力に対して垂直になることがわかりましたので、次に流体内の圧力について考えていきましょう。
考え方としては2つありますので、まずはオーソドックスな教科書とかにも書いてそうな内容からいきましょう。
\(x\)軸と\(y\)軸を図のように取り、各方向に対して微小領域を作ります。
まずは\(x\)軸から。
微小領域の側面にかかる圧力を考えましょう。
左側面の圧力を\(p_x\)とすると、右側面の圧力は以下のように書けます。
\[p_x+\frac{\partial p_x}{\partial x}dx\]
偏微分が出てきていますが、これは\(x\)方向に変位した時に圧力がどれくらい変わるかを示しています。
いわゆる変化の割合、傾きというものですね。
今、微小長さ\(dx\)だけ移動しているので、偏微分の部分に\(dx\)をかけることで、
\(dx\)変化した時の圧力変化分が求まるというわけです。
今、相対的な静止状態を考えていますので、力のつり合いが成立します。
外力として\(x\)軸方向にかかるものは慣性力\(ma\)ですので、圧力がかかっている面積を\(dA\)として、つり合いを考えると
\[p_xdA-(p_x+\frac{\partial p_x}{\partial x}dx)dA-ma=0\]
ここで、\(p_x\)の項は消えますね。さらに質量の部分ですが、微小領域の質量を指していますので、密度をρとすると、
\[m=ρV=ρdAdx\]
このようになり、先ほどの力のつり合いの式で、\(dA、dx\)も消去することができ、
\[\frac{\partial p_x}{\partial x}=-ρa\]
となります。
つまり、\(x\)方向の圧力の変化の割合は\(-ρa)\となり、進行方向側の流体の方が圧力は小さくなるわけですね。
さて、次は\(y\)軸方向の圧力変化ですが、同様に考えることができます。
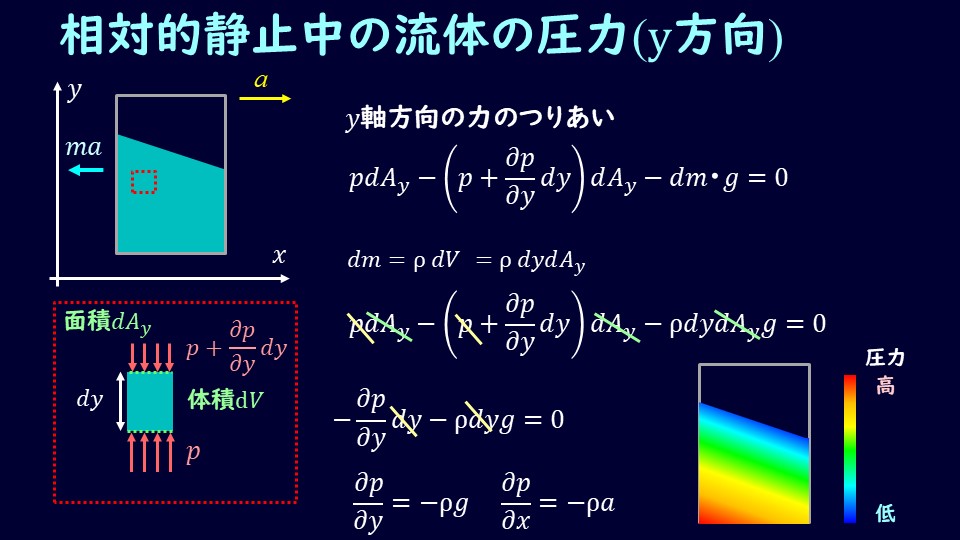
\(y\)軸方向にかかる外力としては重力のみですね。よって、
\[p_ydA-(p_y+\frac{\partial p_y}{\partial y}dy)dA-mg=0\]
と、\(x\)方向の式と同じような式を得ることができます。
式変形も同じようにすればよく、
\[\frac{\partial p_y}{\partial y}=-ρg\]
となりますね。
このように\(x\)軸方向も\(y\)軸方向も一次関数的に変化し、圧力分布を図示すると下図のようになります。
以上がものすごく丁寧に説明したバージョンです。
もっとざっくりイメージする方法を次に紹介します。
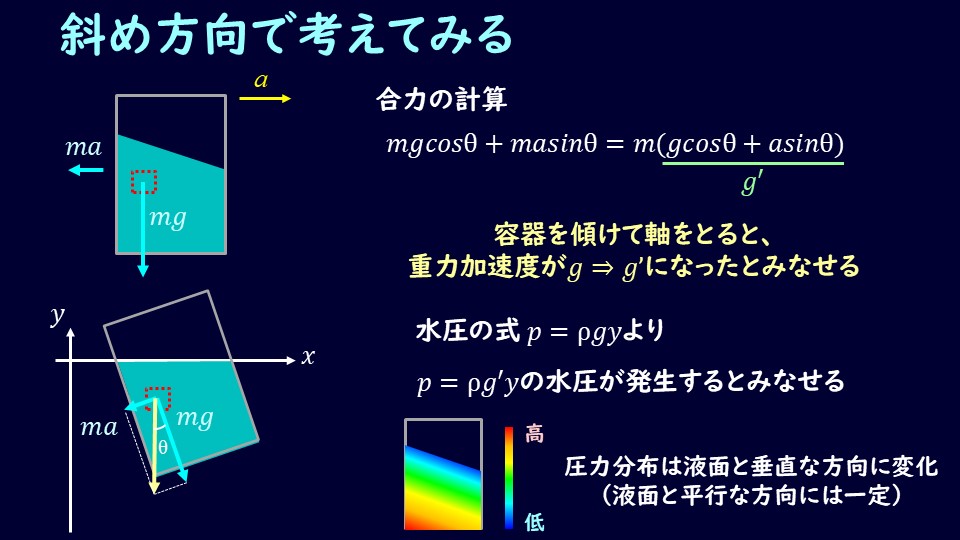
今、流体には重力に加えて、慣性力がかかっていて相対的に静止している状態です。
重力だけの場合の圧力は水圧だけ考えたら良いので楽ですね。
慣性力という別の力があるからややこしいわけです。
で、あれば重力と慣性力を合成して、合力の方向に軸を取り直しましょう。
そうすると、合力と垂直な方向は水面と平行になり、この方向には外力は作用していないことになります。
で、あれば合力の方向のみ考えるだけでよく、
\[mgcosθ+masinθ=m(gcosθ+asinθ)\]
となります。
この式をジーッと見てみると質量×加速度という式になっていることがわかりますね。
慣性力がかかる前は、重力加速度\(g\)だけだったのですが、慣性力がかかったことで、\(gcosθ+asinθ)\という重力加速度に変化した、ともみなせます。
これを新たにg'とでも置き直すと、水圧の式が使えますね。
つまり合力の方向の深さを\(h\)とすると、圧力は、
\(ρg'h\)となります。
以上で相対的な静止状態での流体の圧力がわかったということになります。
まとめ
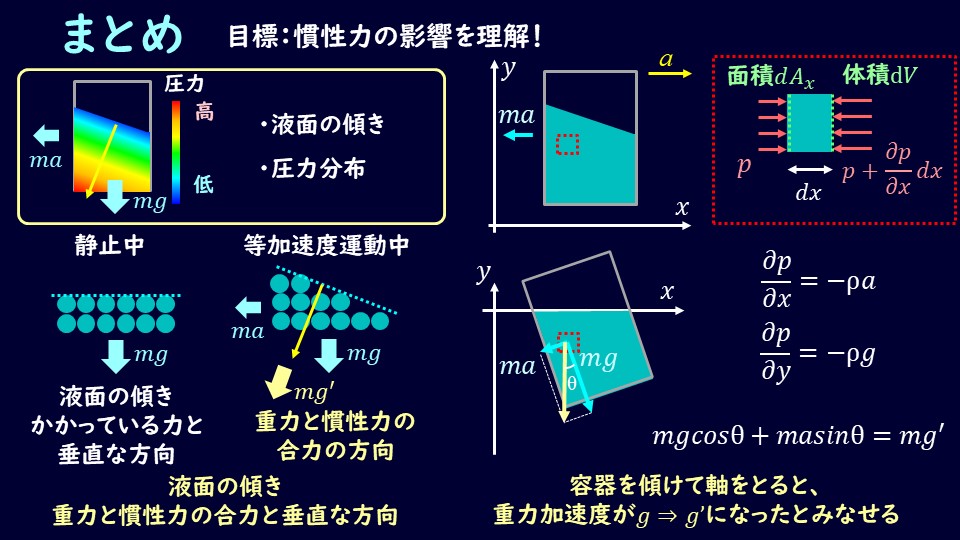
相対的に静止している流体の液面、圧力について解説しました。
慣性力がかかることによって、液面、圧力分布が傾くことになりますので、しっかりとイメージできるようにしておきましょう。
