このU字管みたいなやつなんなの?


あぁ、マノメーターだね。圧力を測るためのもので、よくテストとかでも出てくるから解説しておくね。
今回はマノメーターについて解説します。
流体の圧力を測るためのものなのですが、色んな形状のものがあったりで混乱する方も多いのではないかと思います。
原理をしっかりと押さえて、色んなパターンに対応できるようにしておきましょう。
動画でも解説しておりますので、参考にしていただければと思います。
復習:高さと圧力の関係
気圧であったり、水圧であったり、流体の深さ(高さ)によって感じる圧力が変わってきます。
前々回、水圧については復習していて、次のような式で表すことができるのでした。
\[p=ρgh\tag{1}\]
\(ρ\)は流体の密度、\(g\)は重力加速度、\(h\)は水面からの深さです。
水圧は深くなるほど大きくなるのでしたね。
トリチェリの真空
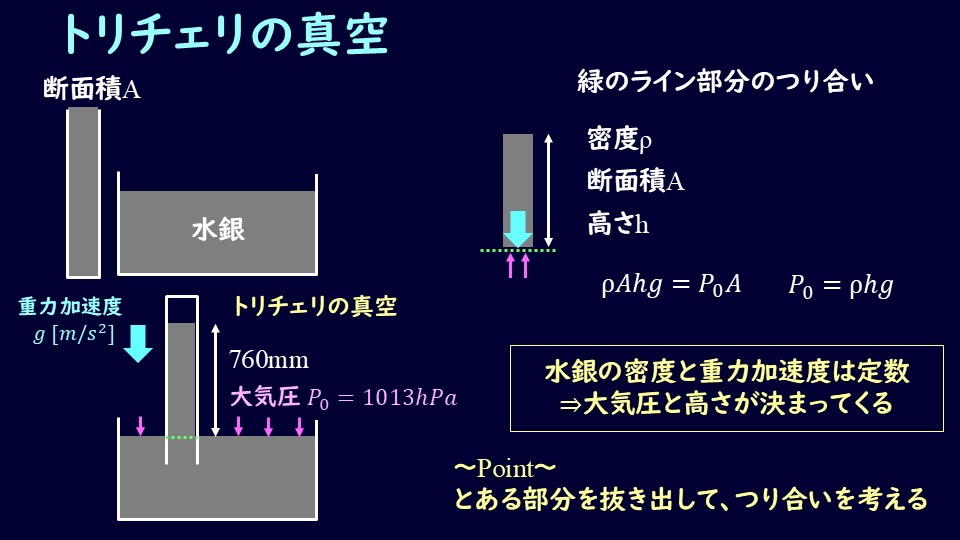
中学の理科の教科書とかでも出てくるかもしれませんが、簡単に大気圧の測定ができるものです。
図のように、管の中を水銀で満たして、その高さを測ることで大気圧を測ります。
大気圧が1013hPaのとき、水銀の液面からの高さは760mmとなります。
このとき、管の中にできた空間部分をトリチェリの真空と呼びます。
なぜこのように決まった高さになるのかというと、大気圧と水銀による重力のつり合いを考えれば理解できます。
管の中には大気が存在しないので、ひっくり返した管の中に入っている水銀にかかっている力は、自身の重力のみと考えることができます。(摩擦とか細かいものは無視しています)
一方、外側の大きな水槽の水銀には大気圧\(P_0\)が発生しているので、
管の中における水槽の水面の高さでの力のつり合いを考えると、管の断面積を\(A\)として、
水銀の密度を\(ρ\)、重力加速度を\(g\)、高さを\(h\)とすると、
\[ρghA=p_0A\tag{2}\]
となります。\(A\)を両辺から消去して
\[ρgh=p_0\tag{3}\]
と書けますね。
(3式より水銀による水圧\(ρgh\)と大気圧\(P_0\)がつりあっていることがわかります。
この水銀による水圧は高さによって変わってきますが、大気圧が一定であれば、高さも一定となります。
この大気圧を1013hPaと一定にしたときの水銀の高さが760mmということですね。
ちなみに面積とかの成分なども式には入っていないので、管の面積なども関係なく、
水銀の高さは760mmとなります。
2つの流体が存在する時

分離するサラダドレッシングみたいな状態を考えましょう。よく混ぜないといけないドレッシングね。
(単純に空気と水で、絶対圧力を考えるイメージでもオッケーです)
とりあえず異なる流体がある場合、圧力がどうなるかを考えましょう。
水圧なり気圧なり、これらは結局のところ、流体が上に積み重なっていて、それらの重力が合わさって作用していると考えることができるのでした。
要するに、下側の流体の圧力を考える際は、
単純にそれぞれの流体からの圧力を足し合わせたらよいということになります。
ひとつ目の流体の密度と高さを\(ρ_1、h_1\)、2つ目の流体の密度と高さを\(ρ_2、h_2\)とし、重力加速度を\(g\)とすると、床面にかかる圧力は
\[(ρ_1h_1+ρ_2h_2)g\tag{4}\]
となります。ほんとにただ足し合わせただけですね。
ちなみに上側の流体の圧力を求めるときには上側のみの圧力を考えればOKです。
これは水圧の起源が、考えている点より上側の流体の重力によるものだからですね。
U字マノメーター
単純なマノメーター
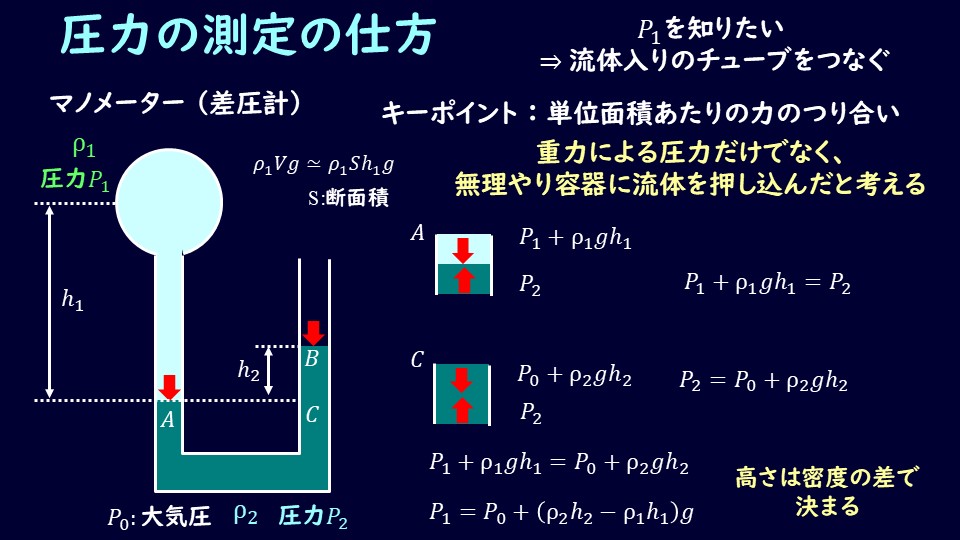
お待たせしました、マノメーターの問題に取り掛かりましょう。
まずは単純なマノメーターから。
マノメーターはそもそも差圧計と呼ばれ、高さの差から圧力を求める計測機器になります。
流体の圧力を知りたいときは、管をつないで高さの差を見る、という形で測定します。
記事の最初の方で取り扱ったトリチェリの真空と同じような考え方が基本ですね。
さて、上図左側のような丸底フラスコを逆さにしたものに薄い水色の液体が入っているとして、薄い水色の液体による圧力\(P_1\)を測定することを考えます。
この逆さにした丸底フラスコには流体がぎゅうぎゅうに押し込まれている状態で、あとから濃い水色の管が繋がれた、というようなイメージを持っていただければと思います。
ガスボンベとかが近いかもですが、単純に丸い部分に何かしら流体が勢いよく流れ込んできている状態がよくある形かもしれません。
なにはともあれ薄い水色の流体の圧力\(P_1\)を求めましょう。
さて、どういう風に考えていくかというと、まずは異なる流体が接している界面に着目しましょう。
図のA点では、薄い水色の流体と、濃い水色の流体が接している面となっており、ここの圧力を考えます。
薄い水色の流体の密度と濃い水色の流体の密度をそれぞれ\(ρ_1、ρ_2\)とし、A点の高さを\(h_1\)とすると、
パスカルの原理から圧力は一定なので、
\[P_1+ρ_1gh_1=P_2\tag{5}\]
となります。なお、\(P_2\)は界面部分の濃い水色部分の圧力を示します。
次にB点の位置を考えましょう。
ここは濃い水色が大気と接している面で、大気圧\(P_0\)がかかっていることになります。
このB点がA点より高い位置にあるのは、濃い水色の流体が薄い水色の流体に押し込まれているためであり、その高さの差を\(h_2\)とします。
右側の管のA点と同じ高さの点をC点とすると、C点での圧力は
\[P_0+ρ_2gh_2=P_2\tag{6}\]
と書くことができます。
左辺は界面の上側から下側に向かって作用する圧力で、大気圧\(P_0\)とB点とC点の間にある流体の重力(C点における水圧)\(ρ_2gh_2\)の和となっています。
この圧力はC点と同じ高さAである点における、濃い水色の流体の圧力\(P_2\)に等しくなりますので(6)式が成立するわけですね。
あとは(5)(6)式をつないであげて、
\[P_1+ρ_1gh_1=P_0+ρ_2gh_2\]
となるので、変形して
\[P_1=P_0+(ρ_2h_2-ρ_1h_1)g\tag{7}\]
となり\(P_1\)が求まります。
2連マノメーター
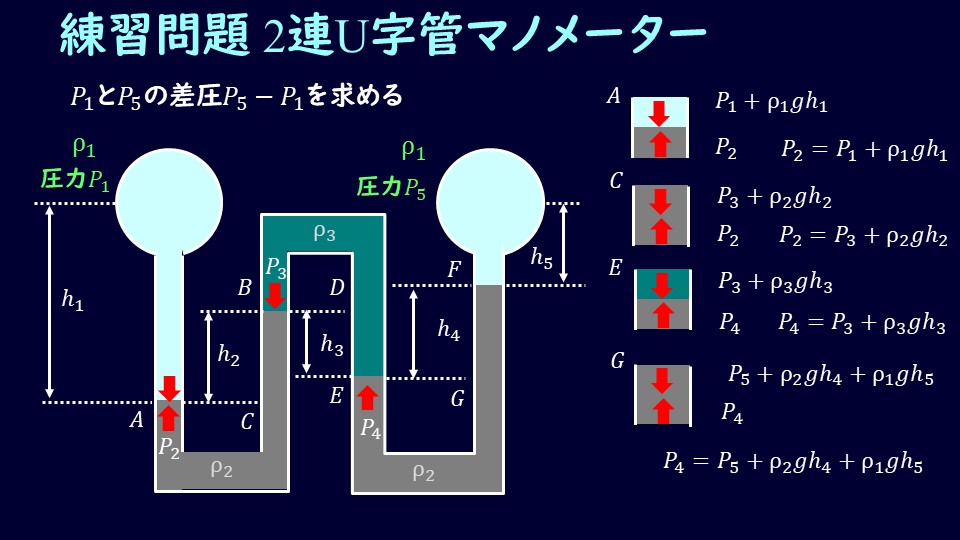
次は2連のU字管マノメーターです。
圧力\(P_1\)と\(P_5\)の差圧を求めましょう。
解き方は先ほどの単純なU字管マノメーターと同じです。
順々に流体界面の圧力を見ていき、それらがパスカルの原理より等しくなっていることを使っていく感じになります。
まずはA点から見ていきましょう。薄い水色の流体が高さ\(h_1\)、密度\(ρ_1\)で満たされているとして、灰色の流体の圧力を\(P_2\)、重力加速度gとしますと、
\[P_2=P_1+ρ_1gh_1\tag{8}\]
となります。
次にB点を見てみます。B点での濃い水色の圧力を\(P_3\)としておきます。このB点とA点の高さの差を\(h_2\)とし、B点側にC点を置きます。
このC点での圧力を考えると、灰色の流体の密度を\(ρ_2\)として
\[P_2=P_3+ρ_2gh_2\tag{9}\]
と式を得ることができます。
まだ行きます。D点を考えるのですが、D点は濃い水色の流体がある管の右側の部分で、B点と同じ高さにある点です。
この点ではB点と同じく圧力は\(P_3\)となっています。
それを踏まえて、E点ですが、E点は濃い水色と灰色の流体の境界で、管の右側の方になりますね。
ここでの圧力を考えると、灰色の流体の圧力を\(P_4\)、濃い水色の流体の密度を\(ρ_3\)とし、D点からの距離を\(h_3\)とすると
\[P_4=P_3+ρ_3gh_3\tag{10}\]
となります。
次はF点ですが、F点は右側の薄い水色の流体と灰色の流体の境界になっており薄い水色の流体の圧力が\(P_5\)、高さが\(h_5\)となっています。
ちなみに右側の薄い水色の流体の密度は、左側の薄い水色の流体の密度と同じく\(ρ_1\)としています。
点Fでの圧力は、
\[P_5+ρ_1gh_5\tag{11}\]
と書くことができますね。これを踏まえて最後にG点を考えると、G点はE点と同じ高さにある一番右側の管の点で、F点からの距離を\(h_4\)とします。
また、右側の灰色の流体の密度は左側の灰色の流体の密度と同じく\(ρ_2\)としており、(11)式も踏まえて、F点での圧力\(P_4\)は
\[P_4=P_5+ρ_2gh_4+ρ_1gh_5\tag{12}\]
と書き表すことができます。
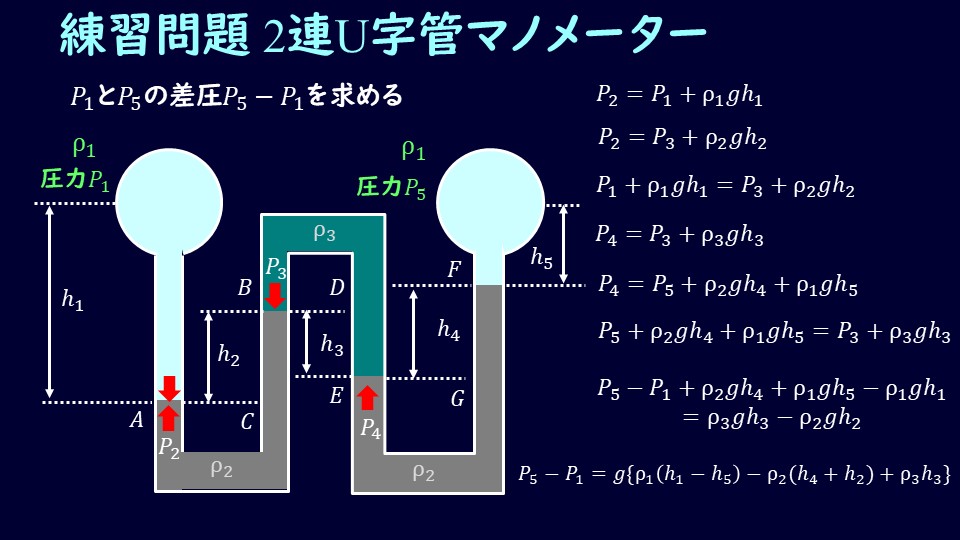
以上で4つの式を得ることができました。4つの式は
\[P_2=P_1+ρ_1gh_1\tag{8}\]
\[P_2=P_3+ρ_2gh_2\tag{9}\]
\[P_4=P_3+ρ_3gh_3\tag{10}\]
\[P_4=P_5+ρ_2gh_4+ρ_1gh_5\tag{12}\]
の4つで、未知数が\(P_1~P_5\)の5つです。未知数5つで式4つなので、完全に解くことができませんが、今欲しいのは\(P_5-P_1\)の差圧なので、式4つで求めることができます。
なので、あとはこれらの連立方程式を解いていくだけですね。
(8)式と(9)式から\(P_2\)を消去して、
\[P_1+ρ_1gh_1=P_3+ρ_2gh_2\tag{13}\]
(10)式と(12)式から\(P_4\)を消去すると
\[P_3+ρ_3gh_3=P_5+ρ_2gh_4+ρ_1gh_5\tag{14}\]
となります。
さらに(14)式-(13)式とすると、\(P_5-P_1\)という差圧が出てきて、\(P_3\)も消去することができますね。
よって(14)式-(13)式は
\[P_5-P_1+ρ_2gh_4+ρgh_5-ρ_1gh_1=ρ_3gh_3--ρ_2gh_2\tag{15}\]
となって、これを整理すると
\[P_5-P_1=g(ρ_1(h_1-h_5)-ρ_2(h_4+h_2)+ρ_3h_3)\tag{15}\]
と差圧\(P_5-P_1\)を求めることができます。
めでたしめでたし。
まとめ
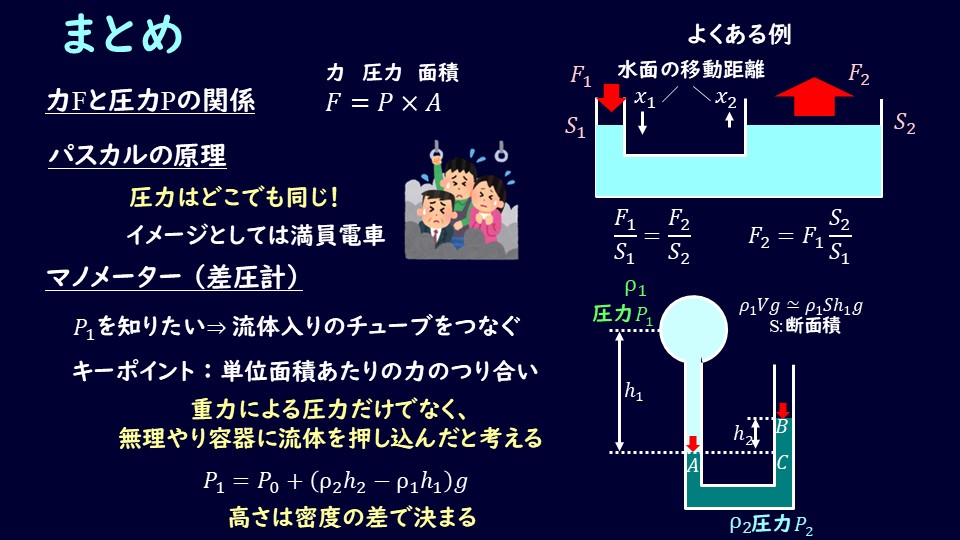
マノメーターの基礎について学習しました。いくつか問題を解くことで、各場所での圧力がどのようになっているか、直感的にもわかってくると思いますので、ぜひ一度は自分の手で問題を解いていただくことをお勧めします。
