流体力学って難しいよね…なんでこんなに難しいんだろう。


身近な例も多いからとっつきやすいんだけど、数式とか難解でイメージしにくい部分が多いからかな。とりあえず全体像をしっかりと把握して、地道に理解していこう。
今回から流体力学シリーズの解説をしていきます。
今回は、流体力学って何?どういった勉強をするの?っていうことを全体像として説明していきますね。
授業を聞いてても、今どういった部分の学習をしてるのっていうことがわかっていないと、全然入ってこないってことがあると思いますので、この記事で全体像をしっかりと把握してもらって、流体力学の勉強の助けになればと思います。
基本的にはYouTubeで動画投稿している内容に沿っての解説となります。
図などは講義で使用しているスライドがメインになりますのでご承知おきください。
流体力学で学ぶ範囲

固体、液体、気体というのを学校で習った人もを多いと思います。
物質は基本的に上記3種類に分類されるのですが、流体力学で扱うのは液体・気体の2つです。
液体とか気体とか、これらは形が一定に定まっておらず、力学的にどういう風に扱っていくかが難しいポイントになり、これらのよくわからない動きをしそうな流体の運動を考える学問が流体力学です。
そりゃ難しいよーっていう意見も納得ですね。
力学でも質点系だと簡単なのに、剛体とか連続体になると途端に難しくなるのとよく似た感じです。
で、流体力学の中でもいろんなすみわけがされている学問であり、流体が止まっている状態の分野を流体静力学といったり、圧力・温度による膨張を無視した分野を水力学、と言ったりします。
まぁこの辺の細かいすみ分けは特に覚える必要がなく、流体力学は結構広い範囲をカバーしていて、その中でもいろんな分野があるというイメージを持っていただければと思います。
この講義シリーズでは、流体が止まっている流体静力学も含めて流体力学を勉強していきたいと思います。
具体的にどういうものを扱うか

キーとなるのは粘性・圧縮性・流れ方です。
粘性はさらさらしているか、ドロドロしているかといったところです。
水に比べてはちみつとかドロっとしていますね。
圧縮性はめちゃくちゃ速い流れとか、密度が変化するような状況のときに現れます。
例えばジェット機の周りの空気などです。
流れ方はさらーっと流れるようなものだったり、川が氾濫しているような乱れた流れとか、渦巻いてたりとか、いろんな流れ方があります。
流体力学は上記のようなことについてどんな式で表すことができるかなーって考えるわけですが、いろんな仮定を入れながら、運動状態を単純化していくようなことをしていきます。
ただ、その仮定の仕方がいろんな種類があって、結構限定的だったりするので、ごっちゃにならないように、ちゃんと整理しながら勉強していかなければいけないわけですね。
というわけで、しっかりとまずは全体像を見て、どういうことをやっていくのかな~っていうのをざっくりと理解していきましょう。
流体力学の全体像
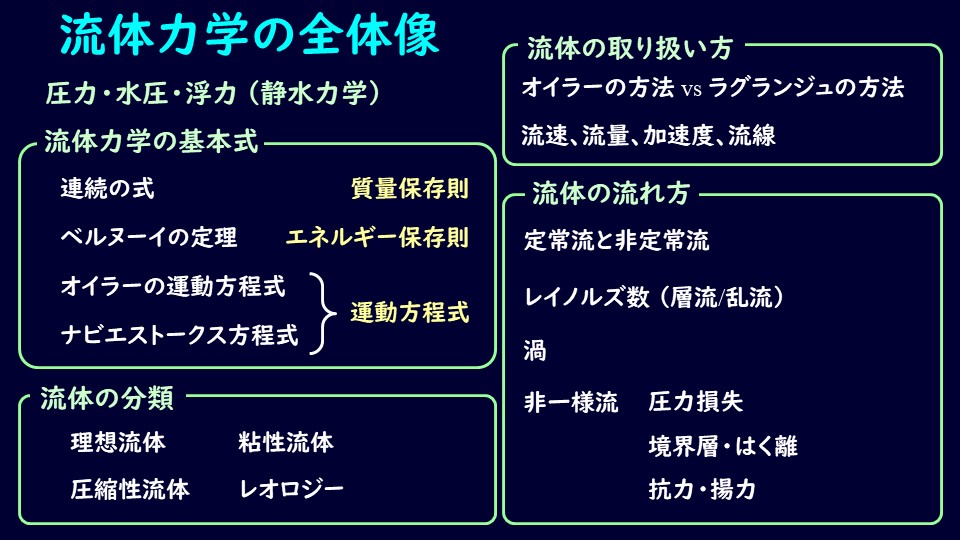
いろんな教科書とかを見て、おおよそこんな流れで勉強していきますよ~っていうのを示していきます。
静水力学の分野
まずは静水力学の内容です。
高校物理でも圧力、水圧、浮力といった内容は習うと思いますが、基本的には流体が止まっているときの力について理解していきます。
高校物理で習ったから大丈夫だよーって思ったそこのアナタ!
高校レベルでは踏み込まなかったレベルが流体力学にはあります!
微分積分を使ってより一般的な物体に対してかかる力を考えていくことになります。
この静水力学の分野を乗り越えたのちには、流れる物体を考えていくことになります。
流体力学の基本式
この辺りからようやく流体力学っぽい!って感じる方もいらっしゃると思います。
そして流体力学にも基本式というものが存在しています。
え?基本式?そう、力学ではニュートンの運動方程式とかエネルギー保存則とかがそれにあたるのですが、流体力学にもあるんです。
それが連続の式、ベルヌーイの定理、オイラーの運動方程式、ナビエストークス方程式といったものたちです。
連続の式は質量保存則、ベルヌーイの定理はエネルギー、オイラーの運動方程式とナビエストークス方程式は運動方程式に相当します。
運動方程式だけ2種類あるのが不思議に感じるかもしれませんが、少し前に説明した通り、流体力学にはいろんな仮定をいれて流体の運動を記述します。
今はその仮定が異なるため2種類存在していると考えてもらえればよいです。
仮定を入れるといっても、どういった場合にどういった仮定をいれるのか、といったところが大事になっていますね。
そこで、流体の分類を詳しく見ていくことになります。
流体の分類
これは先ほど説明した粘性、圧縮性といった話ですね。
粘性、圧縮性がないような流体を理想流体と呼んでいます。
また粘性の中にもいろんな分類があります。
はちみつとマヨネーズでは粘り方が少し違ったりしますよね。
粘性をもっと詳細に分けて物理的な挙動を議論していく分野をレオロジーと呼びます。
今回のシリーズではあまり深くレオロジーの話まで踏み込みませんが、そういった分野があるといったことを認識してもらえればOKです。
また、圧縮性についても結構特殊なケースで考えることが多いので、こちらもあまり深く解説しません。
この流体力学のシリーズでは粘性をメインに取り扱っていくことになります。
これらの分類をしっかりと頭に入れたうえで、どういう風に取り扱っていけばよいかという話になります。
流体の取り扱い方と流れ方
そもそも流体をどのように見ていくのかという視点の問題があり、それがオイラーとラグランジュの方法の2つです。
待ち伏せ型か追跡型かとも呼ばれるものですが、どちらも大事な見方になりますので、しっかりと説明できるようにしたいと思います。
また、取り扱うにあたって、流体力学特有の用語や、力学のときと同じような扱いをすると間違えてしまうものがあったりしますので、それらを押さえておく必要があります。
結構、前もって学習しておかなければいけないことが多いですが、しっかりと基礎固めしておきましょう。
基礎的なところをしっかりと理解したら、ようやく流体の流れ方について議論を進めることになります。
定常流や非定常流、層流や乱流、渦、非一様流といった流れをやっていきます。
これらの流れの部分の勉強をしていくと、ポイントとなる用語や考え方がたくさん出てきますので、しっかりと整理しながら進めていくことになります。
レイノルズ数や圧力損失とかがそうですね。
流体力学の難しさ

さて、ここまで流体力学の全体像についてざーっとみてきたわけですが、なかなかボリュームたっぷりで心配になった方も多いのではないでしょうか?
次にどういったところが難しくて注意しなければいけないかについて示していって、力の入れどころをしっかりと把握していきましょう。
現象が複雑
はい、元も子もないことを言っていますが、現実の流体の挙動というのは結構複雑なのです。
理想流体というものがちらっと出てきましたが、理想すぎて現実からかけ離れていて使い物にならないことが多いです。
現実は厳しいのです。そんなに理想論が通じるケースなど少ないんですね。
そもそも運動方程式であるナビエストークス方程式は解析的に解けないのです。
(解となる関数はこうだよ~って解くことができないということ)
そういったこともあり、結局、運動方程式があっても数値解析に頼ったりすることも多いです。
また、流体の状態量を正しく測定することも難しいということも、流体力学の難しさの一つです。
はい、この辺りは一般論的な話です。
ネットで調べたら出てきます。AIも似たようなことを言ってきます。
でもですよ。
この辺の難しさを実感できる人というのは、現実の流体に対して解析を行ったりする人向けの話なんですね。
つまりは研究している人たちや、流体関係の開発などをしている人たち向け。
初心者の学部生の方々が心配するような部分ではないような気がしています。
そう、もっと別のところに難しさがあると。
必要な数学が難しい
はい、これです。
偏微分方程式、ベクトル解析、深いところまでやると複素関数まで。
あとは力学で学んだ内容をところどころアップデートしていかないといけないところでしょうか。
初学者の方々は、しっかりと数学的な取り扱いから物理現象をイメージできるようになるところが最初のステップだと思います。
なのでしっかりと数学的な部分もフォローしながら進めていきたいと思います。
この式はこういうイメージか、と理解した上で、複雑な流体の現象をどう取り扱えばよいかを考えられるようになればよいと思います。
前提とする仮定が多い
あとはこれですね。
情報量過多でごっちゃごちゃになってしまうというケース。
あれ?なんでこのケースではこの仮定じゃないの?この式使うとなんか現実とは違うようなことが起きてる気がするんだけど・・・?とか。
これはしっかりと整理しながらやっていくしかないと思います。
物理的な意味と数学的な知識があれば理解できると思いますので、頑張っていきましょう。
流体力学の応用先
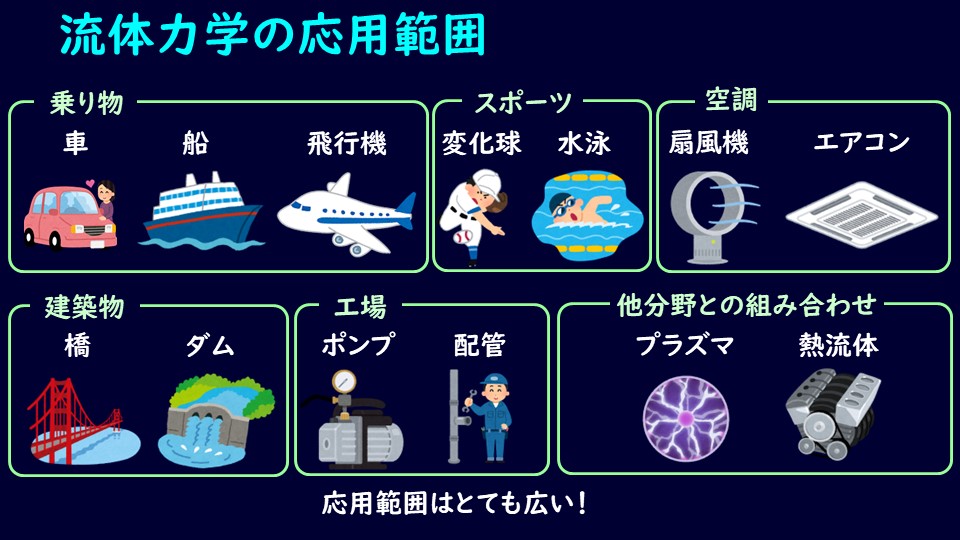
そんな流体力学を学んだあなたには、こんな広い応用先が待ち構えております。
もうよりどりみどりです。
1枚のスライドには書ききれない。
それほど応用範囲は広いのです。
流体力学自体は結構歴史的に古い分野であるにも関わらず、今もなお、専門的に研究がなされている分野でもあります。
つまり深い!そして広い!
流体力学の計算は、力づくで計算しなければいけないとか、結構コンピュータのパワーが必要だったりすることが多いのですが、昨今のコンピュータの進化がすばらしく、また機械学習やAIの発展もあり、いろんな計算方法でいろんな研究が活発になされています。
面白そうと感じてきましたか?
興味が出てきたらぜひ流体力学を一緒に学んでいきましょう!
