うわぁーー!うわさのナビエストークス方程式が出てきたよー!わけわかんないぃ!


とりあえずちょっと落ち着こうか。
さて、今日はナビエストークス方程式を考えていきましょう。
ここまでの理想流体の話や粘性流体の基礎的なところを理解できていれば、丁寧に見ていくことでナビエストークス方程式の中身を理解できると思いますので、頑張っていきましょう。
ナビエストークス方程式
まず、前提として密度と粘度が一定の流体を考えます。
非圧縮かつ粘性流体、という状態ですね。
ここまで色々な粘性流体の流れを見てきました。
クエット流れであったりポアズイユ流れであったり…

これらの流れ方について、流速を求めていたのですね。
また流速を求めるにあたって圧力勾配について何かしらの仮定を入れて求めていました。
そのため、圧力や流速を求めることによって、具体的な粘性流体の流れ方がわかる、ということになります。
その圧力や流速を求めるような方程式がナビエストークス方程式です。
ナビエストークスの中身
ナビエストークス方程式の形を先に示しておきますと、具体的な式の形としては
\[ρ\left(\frac{\partial \textbf{v}}{\partial t}+\textbf{v}・∇\textbf{v}\right)=-∇p+μ∇^2\textbf{v}+\textbf{f}\]
となっています。
このままだとわけのわからない文字の羅列に見えてしまいますので、それぞれの項について考えていきましょう。
最初にネタバラシしておくと、理想流体のオイラーの運動方程式を過去の記事で解説しましたが、ナビエストークス方程式はオイラーの方程式に
・定常流の前提を外す
・粘性力を付け加える
という条件を付加したものになっています。
なので、オイラーの運動方程式のときと同様に、運動方程式からナビエストークス方程式を導出していきましょう。
慣性項
これは運動方程式\(ma=F\)の\(ma\)に相当するところですね。
いま単位体積あたりの流体を考えるとして、運動方程式の両辺を体積\(V\)で割ると、
\[\frac{ma}{V}=ρa=f\]
となりますね。
\(f\)は単位体積あたりの力で\(\frac{F}{V}\)としています。
ナビエストークスの方程式にはρが含まれているので、問題になってくるのは加速度\(a\)のところです。
流体力学はオイラーの方法とラグランジュの方法と2種類の見方をするのですが、オイラーの方法で取り扱うことが多いのでした。
このオイラーの方法は待ち伏せ型と呼ばれるような見方になっていて、とあるエリアをずーっと見続けるような見方になっています。
専門的な言い方だと場の量として物理量を扱う、と言ったりします。
このオイラーの方法を取り入れると、とある流体の速度は位置と時刻を設定しないと決まらなくなります。
つまり速度\(\textbf{v}\)が位置\(\textbf{r}\)と時刻\(t\)の多変数関数になっていることになります。
そうすると加速度は速度の時間微分なので、
\[\textbf{a}=\frac{d\textbf{v}}{dt}\]
となりますが、変数が2種類あるので、全微分を考える必要があります。まず微小量の\(d\textbf{v}\)を考えると、
\[d\textbf{v}=\frac{\partial\textbf{v}}{\partial t}dt+\frac{\partial \textbf{v}}{\partial \textbf{r}}d\textbf{r}\]
と書くことができるので、両辺を\(dt\)で割ると、
\[\frac{d\textbf{v}}{dt}=\frac{\partial \textbf{v}}{\partial t}+\frac{\partial \textbf{v}}{\partial \textbf{r}}\textbf{v}\]
となります。
ここで位置の時間による全微分を速度としていて、
\[\frac{d\textbf{r}}{dt}=\textbf{v}\]
となっています。
なので運動方程式は
\[ρ\left(\frac{\partial\textbf{v}}{\partial t}+\frac{\partial \textbf{v}}{\partial \textbf{r}}\textbf{v}\right)\]
となります。
あれ?まだなんか微妙に違うんだけど…


そうだね。位置の微分のところをもう少し変形してみようか。
これまで、位置の変数を\(\textbf{r}\)としていましたが、ここから\(x、y、z\)として考えていきます。
そうすると、速度の成分も3つの成分にわけることができて、\(v_x、v_y、v_z\)と書き表すことができますので、
\[ρ\left(\frac{\partial v_x}{\partial t}+v_x\frac{\partial v_x}{\partial x}\right)\]
\[ρ\left(\frac{\partial v_y}{\partial t}+v_y\frac{\partial v_y}{\partial y}\right)\]
\[ρ\left(\frac{\partial v_z}{\partial t}+v_z\frac{\partial v_z}{\partial z}\right)\]
と各成分を書き直すことができます。
ここで、微分演算子∇を用いると、
\[∇=\left(\frac{\partial }{\partial x},\frac{\partial }{\partial y},\frac{\partial }{\partial z}\right)\]
なので、
\[ρ\left(\frac{\partial \textbf{v}}{\partial t}+\textbf{v}∇・ \textbf{v}\right)=ρ\left(\frac{\partial \textbf{v}}{\partial t}+\textbf{v}・∇ \textbf{v}\right)\]
となります。
運動方程式の力の項
ナビエストークス方程式の形は色んな参考書で微妙に形が違って書かれていますが、
基本的には運動方程式なので、力の項が表れてきます。
この力の項を分解すると
力の種類
- 圧力項
- 粘性項
- その他の外力(重力など)
となります。
ということで、これらの3つを考えていくことにします。
圧力項
それでは圧力項についてです。
この圧力項についての考え方は、これまでの圧力の考え方と同じです。
微小領域を考え、微小領域にかかる圧力を考えます。
図のように微小な体積に対して、\(x、y、z\)軸をとり、それぞれどのような圧力がかかるか書き出してみると、
\[x軸方向: p_xdA_x-\left(p_x+\frac{\partial p}{\partial x}dx\right)dA_x=-\frac{\partial p}{\partial x}dxdA_x\]
\[y軸方向: p_ydA_y-\left(p_y+\frac{\partial p}{\partial y}dy\right)dA_y=-\frac{\partial p}{\partial y}dydA_y\]
\[z軸方向: p_zdA_z-\left(p_z+\frac{\partial p}{\partial z}dz\right)dA_z=-\frac{\partial p}{\partial z}dzdA_z\]
と書き表すことができます。
それぞれ方向の末尾にある微小距離×微小面積を計算すると微小体積\(dv\)となりますね。
よって、
\[x軸方向 -\frac{\partial p}{\partial x}dV\]
\[y軸方向 -\frac{\partial p}{\partial y}dV\]
\[z軸方向 -\frac{\partial p}{\partial z}dV\]
これも微分演算子∇を使ってまとめて書き表わせて、
\[-∇pdV\]
となりますね。
単位体積になおすために\(dV\)で割ると
\[-∇p=-grad p\]
となります。
粘性項
こちらも微小領域を考えることで導出できます。
粘性による力となりますので、微小体積に粘性によってどのような力が発生するか考えていきましょう。
粘性の度合いは粘度で表すことができ、その粘度には動粘度という流体同士のつながり度合いを含んでいました。
つまり、考えている微小体積の周りの流体が動くことによって、微小体積に力がかかってきます。
その中で最もメジャーなものがニュートンの粘性法則で表されるせん断力でした。
それに加えて、図のように隣の流体が動くことによって垂直応力も発生します。

粘性があると流体粒子間に何かしらの相互作用のようなものが働いて、となりの粒子に引っ張られて力を受けるので、面に対して垂直な応力も当然発生しうるわけですね。

せん断力成分
まず微小体積に発生する各方向のせん断力を書き出すことにします。
そもそもせん断力は考えている面内に働く応力なので、面の取り方、発生する応力の方向に注意しながら考えていきましょう。
まず、\(x\)軸方向ですが、関係するせん断力は、\(y\)軸に垂直な面内にかかるせん断応力と、\(z\)軸に垂直な面内にかかるせん断応力になりますね。
せん断応力の添え字のルールとして下記のようにしますと、

\(x\)軸方向に発生するせん断応力はそれぞれ\(τ_{yx}、τ_{zx}\)となりますね。
これらについて、微小距離進んだ部分のせん断応力を考えるのですが、\(τ_{yx}\)については、
\[τ_{yx}+\frac{\partial τ_{yx}}{\partial y}dy\]
となりますね。同様に
\[τ_{zx}+\frac{\partial τ_{zx}}{\partial z}dz\]
と書けますね。
これらに面積をかけて、微小領域の\(x\)軸方向にかかる粘性力は
\[-τ_{yx}dA_y+\left(τ_{yx}+\frac{\partial τ_{yx}}{\partial y}dy\right)dA_y-τ_{zx}dA_z+\left(τ_{zx}+\frac{\partial τ_{zx}}{\partial z}dz\right)dA_z\]
式を整理すると、
\[\frac{\partial τ_{yx}}{\partial y}dydA_y+\frac{\partial τ_{zx}}{\partial z}dzdA_z\]
となります。
先ほどの圧力項の時と同じく、\(dydA_y=dzdA_z=dV\)となりますので、
\[\left(\frac{\partial τ_{yx}}{\partial y}+\frac{\partial τ_{zx}}{\partial z}\right)dV\]
と変形できますね。
さて、ここから各せん断応力に対して、ニュートンの粘性法則を適応していきます。
ニュートンの粘性法則は
\[τ=μ\frac{dv}{dy}\]
と書けました。
この式の意味をしっかりと考えながら、3次元的に流体を考えるとどのようなせん断力が出てくるかを考える必要があります。
よって微小体積のときのニュートンの粘性法則を考えていきましょう。
図のように、3次元的に考えるとせん断応力は6種類発生します。
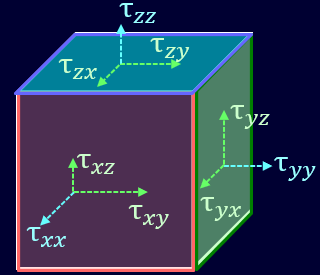

このうち、まず\(τ_{xy}\)を考えましょう。
\(τ_{xy}\)によって\(z\)軸に垂直な面(青色の面)が変形することを考えます。
下図のように青色の面を上から見たとき、\(τ_{xy}\)は青色の面の上下の辺にかかっているように見ることができます。
ここで、せん断応力の向きは上下の辺で逆向きにとることになりますので、このままだとせん断応力によって微小体積が回転してしまうことになります。
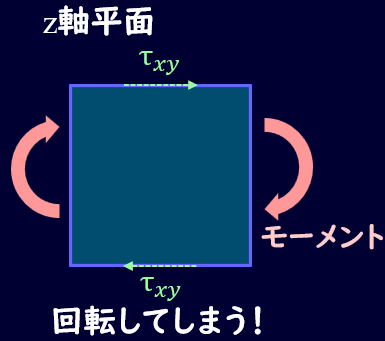
今、この微小体積が回転するケースを考えていないので、このせん断力によるモーメントを打ち消す必要があります。
(回転を考慮すると非常に複雑な話になりますので、ここでは取り扱いません)
そのため、この打ち消すようなモーメントを発生させるために、左右の辺に図のようなせん断力\(τ_{yx}\)が発生します。
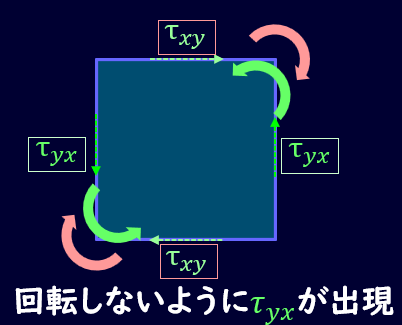
また、これらのせん断力は力のつり合いが必要になってくるので、右の面と左の面にかかる応力は等しくなります。
ちなみに厳密な証明は回転に関するつり合いを考える必要がありますので御注意を。
ここではあくまで簡単な理解のための説明ということで割り切らさせていただきます。
回らないようにしないといけないという理由であれば、上の面にせん断応力が発生すると、左右の面にも応力が発生する、ということは逆も言えるわけで、
左右の面にせん断力が発生しても、上下の面にせん断力が発生するわけです。
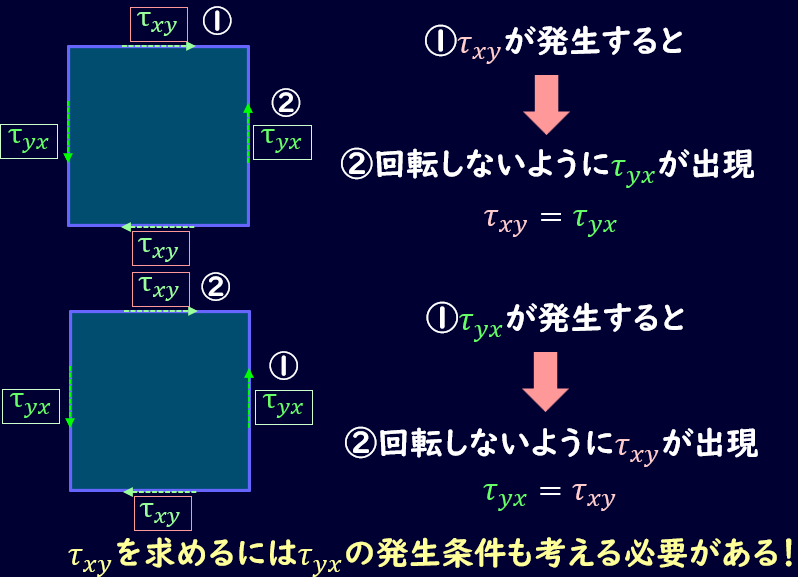
つまり、上の面のせん断応力\(τ_{zy}\)を求めるときには、\(τ_{yz}\)が発生する要因も考える必要があるわけですね。
よってニュートンの粘性法則を考えると、
\[τ_{xy}=μ\left(\frac{\partial v_y}{\partial x}+\frac{\partial v_x}{\partial y}\right)\]
となります。
第2項は\(τ_{yx}\)が発生する条件ですね。
この考え方を\(x\)軸に垂直な面内に発生するせん断力\(τ_{xz}\)で考えるとすると、
\[τ_{xz}=μ\left(\frac{\partial v_z}{\partial x}+\frac{\partial v_x}{\partial z}\right)\]
となります。
ここまでで、せん断力の中身がわかりましたので、、先ほど求めた微小距離変化させた面との差分と合わせていきましょう。
\[\frac{\partial τ_{xy}}{\partial y}=μ\left(\frac{\partial}{\partial y}\frac{\partial v_y}{\partial x}+\frac{\partial^2 v_x}{\partial y^2}\right)\]
となります。
\(τ_{xz}\)についても同様で、
\[\frac{\partial τ_{xz}}{\partial z}=μ\left(\frac{\partial}{\partial z}\frac{\partial v_z}{\partial x}+\frac{\partial^2 v_x}{\partial z^2}\right)\]
となります。
垂直応力成分
さて、せん断応力だけではなく、垂直応力成分も発生するということは先ほど述べた通りでした。
流体力学では垂直応力についてもτを使うことが多いようなので、τを使って垂直応力を書き表すと、\(x,y,z\)方向の垂直応力は\(τ_{xx}、τ_{yy}、τ_{zz}\)と表すことができます。
これらも隣接する流体素片の移動速度によって力を受けるとすると、先ほどのせん断応力の式と同じ形式で書き表すことができます。
\(x\)軸成分は
\[τ_{xx}=μ\left(\frac{\partial v_x}{\partial x}+\frac{\partial v_x}{\partial x}\right)\]
と書くことができます。
これもニュートンの粘性法則の一種ですね。
微小体積を考えると発生しているせん断力は
\[-τ_{xx}(x)dA_x+\left(τ_{xx}(x)+\frac{\partial τ_{xx}}{\partial x}dx\right)dA_x\]
と書け、整理すると、
\[\frac{\partial τ_{xx}}{\partial x}dxdA_x=\frac{\partial τ_{xx}}{\partial x}dV\]
となります。
単位体積を考えて、\(dV\)を消去すると
\[\frac{\partial τ_{xx}}{\partial x}\]
となります。
先ほどのニュートンの粘性法則を適用すると、
\[\frac{\partial τ_{xx}}{\partial x}=μ\left(\frac{\partial^2 v_x}{\partial x^2}+\frac{\partial^2 v_x}{\partial x^2}\right)\]
となります。
各方向の力を考える
以上のようにせん断応力と垂直応力を求めることができました。
あとは各方向ごとにかかる力をまとめていきましょう。
まず、\(x\)方向ですが、\(\frac{\partialτ_{xx}}{\partial x}、\frac{\partialτ_{yx}}{\partial x}、\frac{\partialτ_{zx}}{\partial x}\)の3つですね。
よって、
\[\begin{align}&\frac{\partialτ_{xx}}{\partial x}+\frac{\partialτ_{yx}}{\partial x}+\frac{\partialτ_{zx}}{\partial x}\\&=μ\left(\frac{\partial^2 v_x}{\partial x^2}+\frac{\partial}{\partial x}\frac{\partial v_x}{\partial x}+\frac{\partial^2v_x}{\partial y^2}+\frac{\partial}{\partial y}\frac{\partial v_y}{\partial x}+\frac{\partial^2v_x}{\partial z^2}+\frac{\partial}{\partial z}\frac{\partial v_z}{\partial x}\right)\\&=μ\left(\frac{\partial^2}{\partial x^2}+\frac{\partial^2}{\partial y^2}+\frac{\partial^2}{\partial z^2}\right)v_x+μ\frac{\partial}{\partial x}\left(\frac{\partial v_x}{\partial x}+\frac{\partial v_y}{\partial y}+\frac{\partial v_z}{\partial z}\right)\\&=μΔv_x+μ\frac{\partial}{\partial x}∇・\textbf{v}\end{align}\]
と計算できます。
\(y\)方向、\(z方向\)も同様に計算することができ、
\[\begin{align}&\frac{\partialτ_{xy}}{\partial y}+\frac{\partialτ_{yy}}{\partial y}+\frac{\partialτ_{zy}}{\partial y}\\&=μ\left(\frac{\partial^2}{\partial x^2}+\frac{\partial^2}{\partial y^2}+\frac{\partial^2}{\partial z^2}\right)v_y+μ\frac{\partial}{\partial y}\left(\frac{\partial v_x}{\partial x}+\frac{\partial v_y}{\partial y}+\frac{\partial v_z}{\partial z}\right)\\&=μΔv_y+μ\frac{\partial}{\partial y}∇・\textbf{v}\end{align}\]
\[\begin{align}&\frac{\partialτ_{xz}}{\partial z}+\frac{\partialτ_{yz}}{\partial z}+\frac{\partialτ_{zz}}{\partial z}\\&=μ\left(\frac{\partial^2}{\partial x^2}+\frac{\partial^2}{\partial y^2}+\frac{\partial^2}{\partial z^2}\right)v_z+μ\frac{\partial}{\partial z}\left(\frac{\partial v_x}{\partial x}+\frac{\partial v_y}{\partial y}+\frac{\partial v_z}{\partial z}\right)\\&=μΔv_z+μ\frac{\partial}{\partial z}∇・\textbf{v}\end{align}\]
となります。これらをベクトル表記すると、
\[\textbf{f_μ}=μΔ\textbf{v}+μ∇(∇・\textbf{v})\]
となりますが、非圧縮性を仮定すると、\(div \textbf{v}=∇・\textbf{v}=0\)なので、
\[\textbf{f_μ}=μΔ\textbf{v}=μ∇^2\textbf{v}\]
と粘性項を導出できます。
これでナビエストークス方程式の各項が求まりましたね。
まとめ
ナビエストークス方程式の各項の導出を解説しました。
粘性項の部分がなかなかややこしいと思いますが、一度手を動かして追いかけていただくと理解が深まると思いますので、しっかりと理解したい人はがんばって一度計算してみることをおすすめします。
