粘性が入ってくるとややこしくてよくわからないんだけど…


粘性を考慮すると理想流体と大きく変わってくるところも多いので、まずは基本的なところから押さえていこうか。
今回から、流体に粘性を加えて、より現実的な流体を考えられるようにします。
粘性を加えることで、理想流体とは異なる流れ方をするので、どういう物理現象を考えるか、まずは基礎的な部分を押さえましょう。
この記事では、粘性、動粘度、剪断力、ニュートンの粘性の法則を解説し、粘性を考慮したときの簡単な具体例についても説明していきます。
粘性
まずは粘性のイメージについてです。
はちみつとか納豆とかネバネバしたものには粘性があるわけですね。
粘性は物体の動きを妨げる向きに作用する力で、図のようなイメージになります。
この粘性は基本的にはどんな流体でも現実には存在しており、その粘性の度合いを粘度、あるいは粘性係数と呼びます。
粘度と動粘度
動粘度νは粘度μを密度ρで割った値になっています。
\[ν=\frac{μ}{ρ}\]
これは粘性による力は流体の密度にも依存するためです。
まぁスカスカの流体の中とギューっと詰め込まれている流体の中で動くことを考え、粘性による力を比較したとき、どちらが粘性による力が大きくなるかは想像しやすいのではないのでしょうか?
もちろんギューっと詰め込まれた流体、すなわち密度が高い流体中の方が粘性による力は大きくなりますね。
ということで密度まで考慮したものが粘度、動粘度は密度の影響を除いたもの、となっているわけですね。
ニュートンの粘性の法則
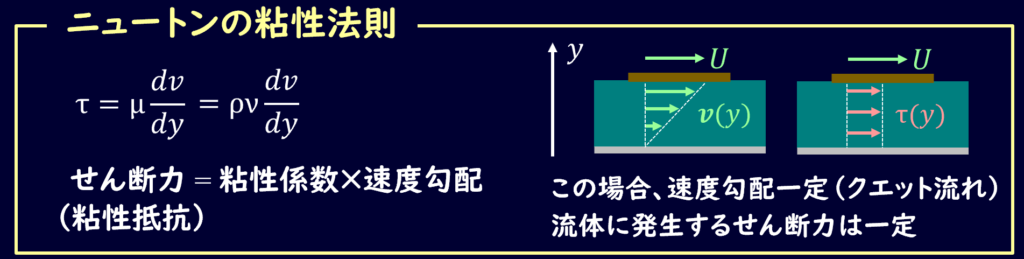
さて、粘性を持つ流体は、流体同士に力を及ぼし合うことになります。
ニュートンの粘性の法則は、流体にかかる剪断応力\(τ\)と粘度\(μ\)、流速\(v\)の関係式を表す法則で、
\[τ=μ\frac{dv}{dy}\]
と書けます。
座標軸は図のようにとっています。
流速に垂直な方向に\(y\)軸を取っており、この微分の部分\(\frac{dv}{dy}\)を速度勾配と呼んだりします。
せん断応力??なんかイメージつきにくいなぁ…


じゃあイメージ図を載せておくね。
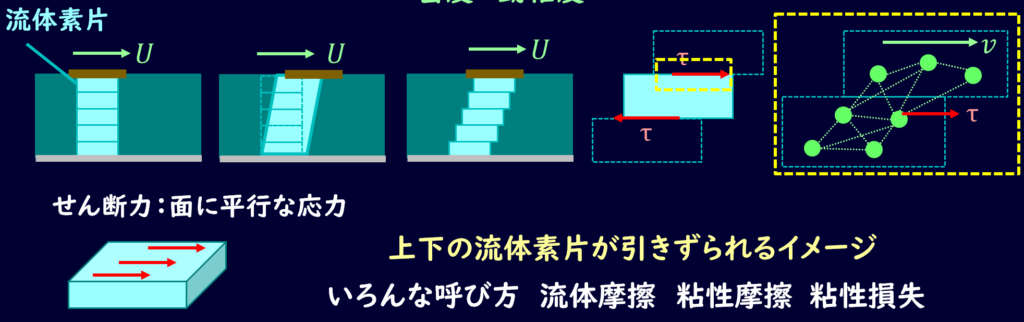
せん断応力は考えている面に対して平行な方向にかかる応力のことを指します。
流体が流れている時には図のような形になりますね。
この流体内部にかかるせん断力を粘性摩擦と呼んだりします。
粘性摩擦を深掘り
ではなぜせん断力が発生するのでしょうか?
これはミクロなレベルで見てみるとイメージしやすいと思います。
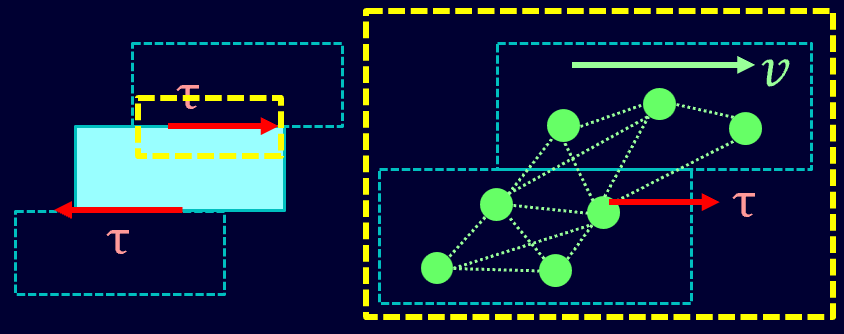
水にも小さいながら粘性は存在しておりますので、例として水分子が流れている状態を考えましょう。
流体として水が流れる際には、水分子同士が相互作用を受けながら流れることになります。
液体の場合、分子同士がゆる〜くつながっているような状態なので、上下で違う速度で分子が動いてしまうと、早い側に引きずられるような力がかかりますね?
この力の向きは流速の向きと同じ向きであり、この力がせん断力に相当するわけです。
ちなみにニュートンの粘性法則は、すべての流体に成り立つわけではなく、ニュートン流体と呼ばれる流体のときに成立します。
これはせん断力の起源がミクロレベルでは相互作用となっているからであり、その相互作用はいろんなものがあるので、単純に速度勾配に比例するものだけではないのです。
ですが、水など結構メジャーな流体であればニュートンの粘性の法則が成り立ち、ニュートン流体として扱えますので、適用範囲はそれなりに広いです。
境界面での流速ゼロ
これは必ず押さえておきましょう。
色々な問題を解く際に、この条件を使って未知数を求めることが頻発します。
で、それってどういうことなの?
なんでそうなるの?っていう疑問が現れると思います。
これもミクロな視点で見てみましょう。
一般的に流体と壁の境界に粘性摩擦がある時、壁の状態は理想的に平ではなく、凸凹したような形状になっています。
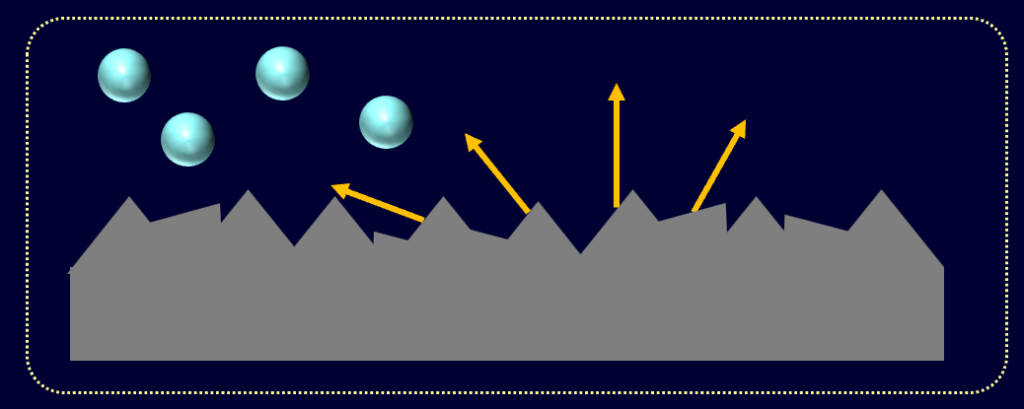
そうすると、流体分子が壁の凸凹に当たるとどのようになるでしょう?
色んな方向に流体分子が飛んでいくことになりますね。
完全にランダムに凹凸があるとすると、飛んでいく方向も完全にランダムになります。
それを巨視的にみると、こんな感じになります。
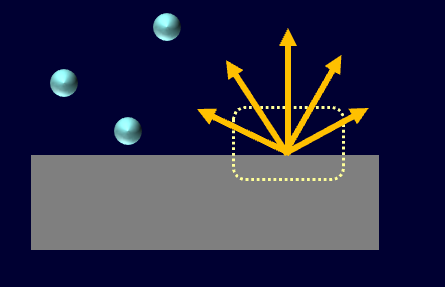
さて、この飛んでいった方向、ベクトルにして全部足して平均取ってあげるとどうなるでしょう?
答えは水平方向の成分は打ち消されて垂直方向の成分しか残らなくなりますね。
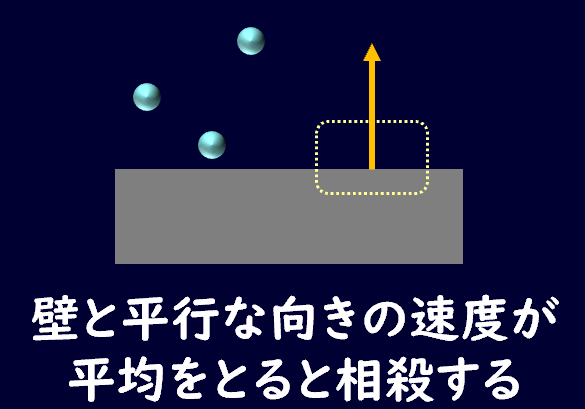
つまり、壁と平行な方向の流速はゼロとなるわけです。
この条件を使って問題を解くことが多いので、しっかりと頭に入れておきましょう。
粘性流体の流れ方
層流と乱流
粘性の話が出てきましたので、粘性を加味した時に現れる流れの代表例として、層流と乱流についても触れておこうかと思います。
図で書くと下図のような流れを層流、乱流と呼びます。
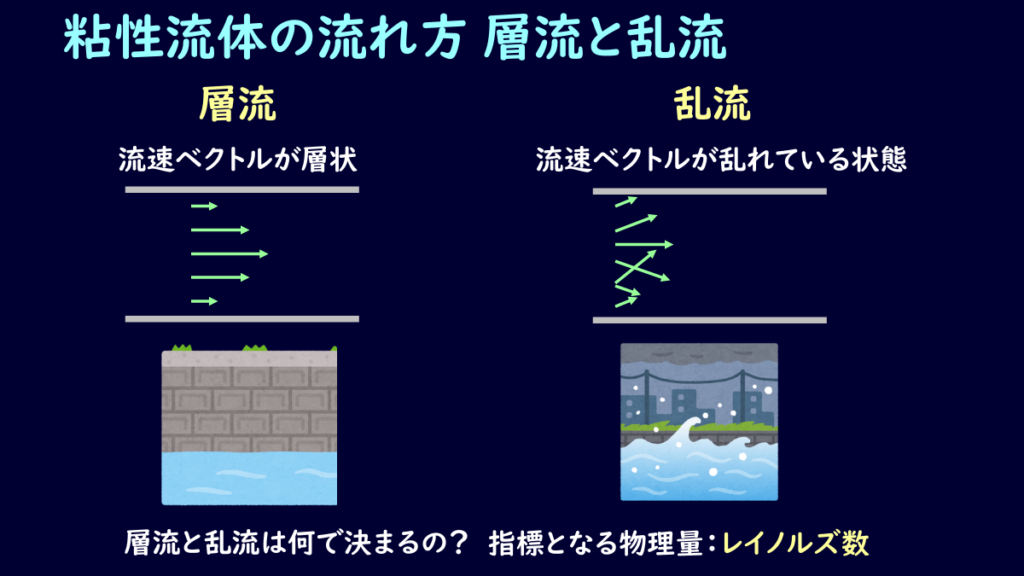
見るからに乱流の方が動きが複雑で難しそうですよね?
最初のうちは簡単な層流を仮定して、しばらくは粘性流体の取り扱いに慣れていただければと思います。
層流は流れが層状になっている乱れの無い流れというイメージを持っておきましょう。
レイノルズ数
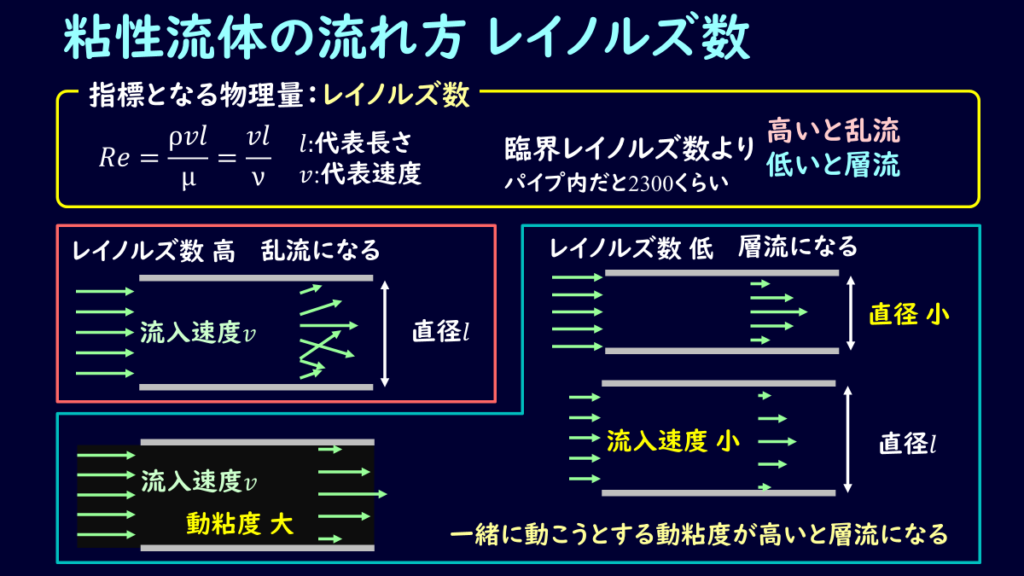
さて、層流と乱流を決めているパラメータは何かということについて説明しましょう。
結論、レイノルズ数というものが層流・乱流を決める指標になっているのですが、図中のような式になっています。
\[Re=\frac{ρvl}{μ}=\frac{vl}{ν}\]
このレイノルズ数が臨界レイノルズ数を超えると乱流になりやすく、低いと層流になりやすくなります。
臨界レイノルズ数に近い状態だとどっちつかずの状態、遷移状態と呼ばれたりします。
この臨界レイノルズ数はどのような構造体に流体を流すかによって決まっており、パイプ内だと2300くらいです。
まとめ
今回は粘性のある流れについて解説しました。
まずは粘度と動粘度の違いとニュートンの粘性法則をしっかりと理解し、層流・乱流がどのようなものかを頭の中に入れておきましょう。
