流体での運動量がよくわからないんだけど…


基本的な考え方は高校物理の考え方と一緒だよ。ただ取り扱いに注意点があるから、そのあたりを解説していくね。
今回から運動量について解説します。
流体力学では取り扱っている対象が流体なので、質点の時と少し異なる部分も出てきますので、違いをしっかりと理解しておきましょう。
流体力学での運動量

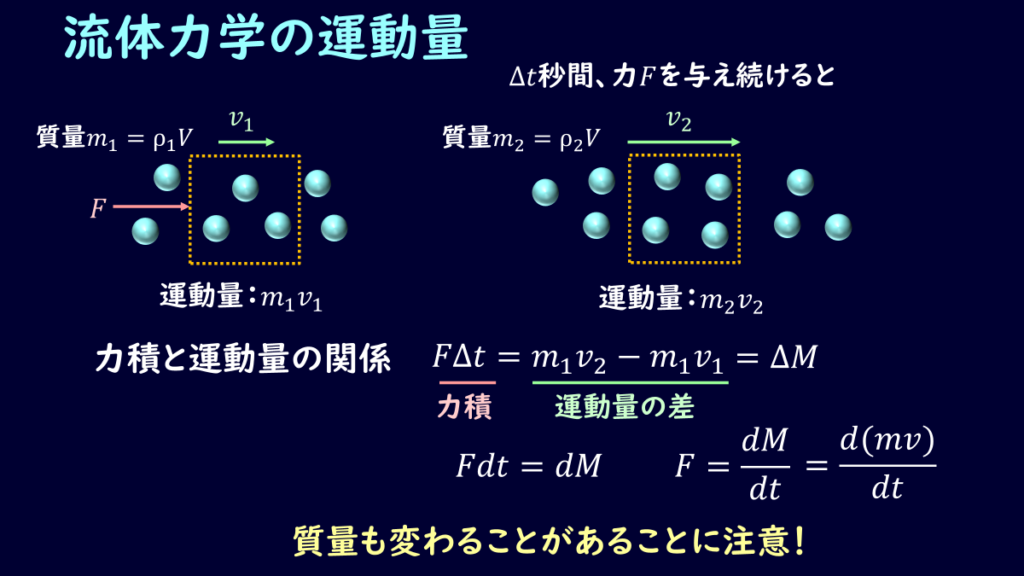
これは高校物理の時と同じで、運動量\(M\)は質量\(m\)と速度\(v\)の掛け算で表すことができます。
\[M=mv\]
次に高校物理の力積を思い出しましょう。
ある時間\(Δt\)の間に力\(F\)を受けた場合の力積は、\(FΔt\)と表すことができます。
この時の運動量変化を\(ΔM\)とし、質点の質量を\(m\)、力を受ける前後での速度をそれぞれ\(v_1、v_2\)とすると、
\[FΔt=ΔM=mv_2-mv_1=mΔv\]
となります。
ここで、質点の質量は力を受けても変化しない、という前提が入っていることに注意しましょう。
ここからある時間\(Δt\)を微小時間\(dt\)と極限をとると、
\[Fdt=mdv\]
となります。
両辺を\(dt\)で割ると、
\[F=m\frac{dv}{dt}\]
となり、力を書き表すことができるわけです。
つまり、運動量の計算から流体による力を計算することができる、ということになります。
ただし、この式は質点で質量が変化しない、という前提の式になっています。
流体を取り扱うときには質量が変化することがあります。
例えば、空気にものすごい力(圧力)をかけると、密度が変化しますね?
注目している領域が一定であれば、空気が圧縮されたりすると、質量が変化するので、その部分を考慮する必要があるわけです。
この時の運動量の微小変化を\(dM\)とすると、
\[Fdt=dM\]
となって、力は
\[F=\frac{dM}{dt}=\frac{dmv}{dt}\]
と書き表すことができます。
これを運動量の法則と呼びます。
質点の時と似ていますが、質量の部分にも微分が入ってくることに注意しましょう。
流体にかかる力の種類

さて、力が運動量を用いて表せるということがわかったので、力の部分について深掘りしていきましょう。
流体を考える際には、質点的に考えるのでは無く、ある体積の流体に着目して考えるのでした。
これを流体素片と言ったりします。
また、オイラーの方法においては、ある体積の部分は固定して考えるような見方をするのでした。
この着目している空間部分を検査体積、あるいは検査領域とよび、その表面を検査面と呼びます。
この検査面を介するような力、すなわち検査面に垂直にかかる圧力や、検査面内に発生するせん断力は表面力と呼ばれます。
一方、検査面を介さないような重力や電磁力は、流体の体積全体にかかる力なので体積力と呼ばれたりするわけですね。
他にも流体が接している部分から受ける反力もあり、トータルで3種類あることを覚えておきましょう。
表面力、体積力、反力の3つですね。
具体例 管路内の運動量
言葉の解説だけだとよくわからないところもあると思いますので、例題を解いて自分のものにしていきましょう。
まずは簡単な水平におかれた断面積が徐々に変わる流管の問題です。
流管内の流体は理想流体で定常流として取り扱います。
検査領域を図のようにとり、検査領域の流体から管路にかかる力を考えることにします。
あれ?流体にかかる力は運動量から求まりそうだけど、流管にかかる力も求まるの?


さっきの3つの力のうち、反力は流体と流管で作用反作用の法則が成り立つので、反力を求めることで流管への力が求まるよ。
ということで、流れとしては
運動量の法則から流体にかかる力\(F\)を求める
流体にかかる力\(F\)を3種類の力に分解して、反力を求める
という2ステップになります。
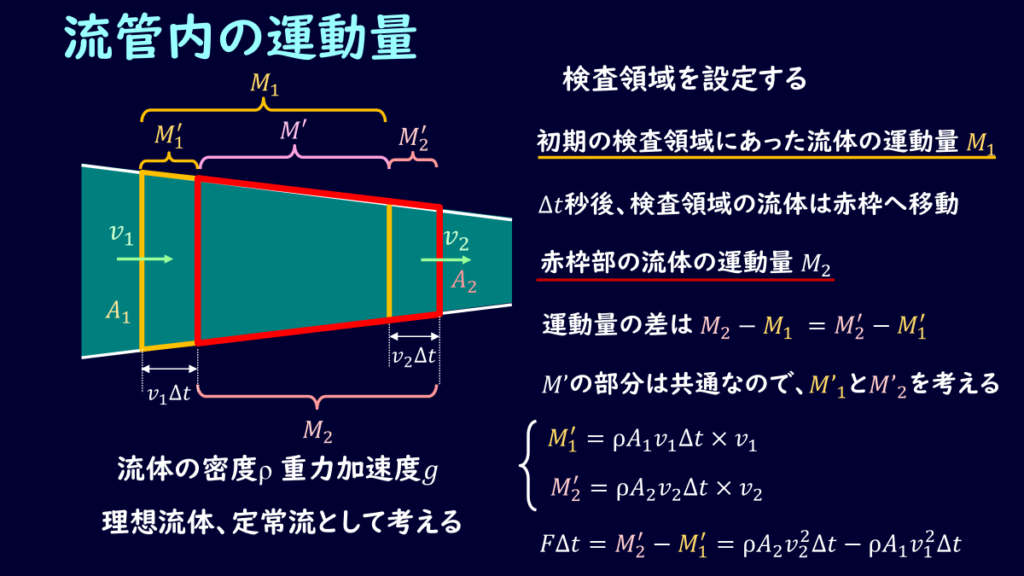
では運動量の法則を考えましょう。
検査領域の左側の面積、流速を\(A_1、v_1\)、右側の面積、流速を\(A_2、v_2\)とします。
検査領域の流体は、とある時間\(Δt\)秒後には図のような赤枠部分のところへ流れていると考えます。
この移動前後の運動量を考えると、まず初期の検査領域にあった流体の運動量は\(mv_1\)、\(Δt\)秒後の赤枠部分では\(mv_2\)となります。
よって運動量変化は、
\[mv_2-mv_1\]
となりますね。
ここで、理想流体かつ定常流を考えていますので、時刻が変わっても観測する位置が同じであれば密度、流速は一定となります。
よって検査領域と赤枠部分で重なっているところの運動量は、運動量変化に寄与しなくなります。
(差を取ったらゼロ)
ということで、運動量変化\(ΔM\)に寄与する部分は図の\(M_1\)の部分と\(M_2\)の部分の差になりますね。
これらの部分の質量について、密度×体積で求めることになりますが、
体積は\(Δt\)を非常に小さな時間とすると、円柱の体積に近似できるので、
\[ΔM=ρ×A_2v_2Δt×v_2-ρ×A_1v_1Δt×v_1\]
となります。
先ほどの運動量の法則から
\[F=\frac{dM}{dt}=\lim_{Δt\to 0}\frac{ΔM}{Δt}=ρA_2v_2^2-ρA_1v_1^2\]
と、力\(F\)を表すことができます。
ここで、体積流量\(Q_1、Q_2\)を使って表すと、
\[F=ρQ_2v_2-ρQ_1v_1\]
と書けます。
外力\(F\)を分解する
さて、ここまでで流体に発生する外力がわかったので、表面力、体積力、反力に分解していきましょう。
流管は水平に設置しているので、体積力である重力などは無視して考えます。
表面力については圧力が作用していますので、流体が流れ出ている部分と入ってくる部分にかかることになります。
入ってくる部分の圧力を\(p_1\)、出ていく部分の圧力を\(p_2\)とすると、表面力\(f_s\)は、
\[f_s=A_1p_1-A_2p_2\]
となります。
外力\(F\)は表面力と反力\(f\)の和で書き表すことができるので、
\[F=f+f_s\]
運動量の法則の式と表面力を代入して、
\[ρQ_2v_2-ρQ_1v_1=f+A_1p_1-A_2p_2\]
流体が外部へ与える力は反力\(f\)と同じ大きさで、向きが逆になるので、\(-f\)を求めればよく、上式を変形して、
\[-f=A_1p_1-A_2p_2-ρQ_2v_2+ρQ_1v_1\]
となります。
この式から、流体が外部へ与える力は面積や密度が与えられている場合、圧力や流量、流速を知れば求めることができる、ということになります。
なんか凄そうだけど、使いこなせる気がしないよ…


次回から演習問題を取り扱うので、そこで慣れていこう
まとめ

運動量の法則について解説しました。
概要は理解できたかと思いますが、使いこなすには慣れも必要ですので、しっかりと次回以降の演習も取り組むようにしていきましょう。
