等加速度運動している容器の中の流体はイメージできるんだけど、回転した場合がよくわからないよ。


流体が回転している状態でも、考え方は同じなので、しっかりイメージできるように解説するね。
今回は等速で回転している流体を取り扱います。
洗濯機の渦みたいなイメージですね。
渦の状態で相対的に静止している状態を取り扱います。
もっと厳密な渦の理論は非常に難しくなるので、ここでは踏みこみません。
液面がどのような形になるのか、圧力はどうなるのかについて解説していきます。
YouTubeでの解説はこちらです。
慣性力について(円運動)

これは前回の記事でも解説していますので、どういったものかについては、前回の記事を参考にしていただければと思います。
今回は円運動しているときの慣性力についてで、いわゆる遠心力ですね。
車がカーブすると外側に力を受ける感覚があると思います。この力が遠心力と呼ばれるものですね。
まず、円運動している物体を外から見てみましょう。
物体は常に移動している方向が変わっていますので、進行方向に対して垂直な向きに何かしらの力を受けていることになります。
とある円の軌道を等速で動くのであれば、中心に向かって一定の力が作用しているとみなせて、これを向心力と呼びます。
これは円運動している物理の外側から見た話で、次はこの円運動している物体に乗ってみましょう。
円運動している物体に乗っているときに、その物体を見てみると止まっているように見えます。
ということは、物体に乗っている人から見ると、向心力と何かの力がつりあって止まっているように見えるわけです。
この向心力とつり合う力が遠心力で、前回の記事でも出てきた慣性力の一種ですね。
遠心力は向心力とつり合うことになるので、円の外向きにかかることになります。
遠心力
さて、遠心力の大きさですが、加速度を考えることになります。
円運動の加速度\(a\)は、円運動の半径を\(r\)、角速度を\(ω\)とすると、
\[a=rω^2\]
と書き表すことができます。
この加速度が円運動の中心に向かってかかっているので、慣性力はその向きと逆にかかると考えて、遠心力\(F\)は
\[F=ma=mrω^2\]
となりますね。
この遠心力が慣性力としてかかってきているとみなして、問題を解いていくことになります。
回転している流体の液面形状
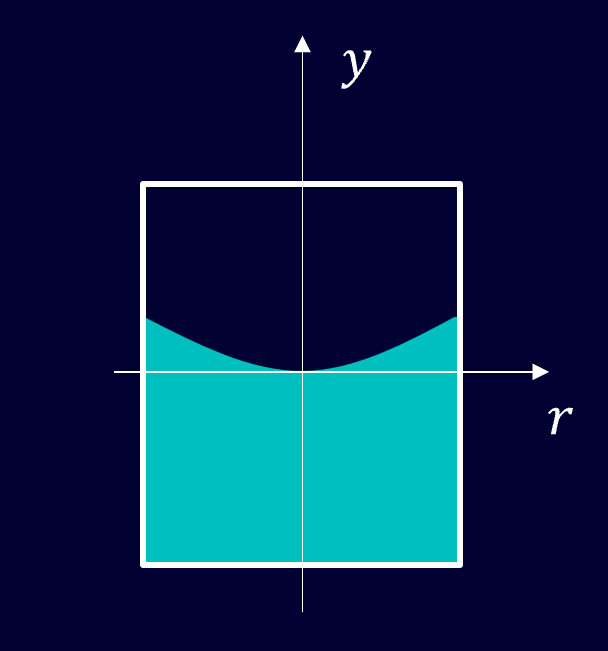
まず、座標軸を設定しましょう。
図のように\(r\)軸と\(y\)軸を取ります。
\(r\)としている理由としては、半径\(r\)の円上では慣性力が等しくなり、対象的に扱えるからですね。
それでは\(r\)方向と\(y\)方向に微小領域をとって、圧力がどのように変化するか見ていきましょう。
\(r\)方向の圧力の微小変化

今、相対的な静止状態を考えているので、微小領域では力がつり合っている状態になっています。
\(r\)方向の力のつり合いを考えると、
\[pdA-(p+\frac{\partial p}{\partial r}dr)dA=F_r\]
微小領域にかかっている力は流体の重力と慣性力の2つですが、\(r\)方向にかかっている力は慣性力だけですね。
なので右辺の\(F_r\)は\(dm×rω^2\)で、微小体積である\(dm\)は密度ρを使って
\[dm=ρ×dAdr\]
となりますね。\(dA×dr\)は微小領域の体積となっています。
よって、
\[pdA-(p+\frac{\partial p}{\partial r}dr)dA=ρdAdr×rω^2\]
となり、両辺からdAを消去して整理すると、
\[\frac{\partial p}{\partial r}=ρ×rω^2\]
となります。
これで\(r\)方向の圧力変化が求まりましたね。
\(y\)方向の圧力の微小変化

同じように\(y\)方向も考えましょう。
鉛直方向には重力のみが作用しますので、
\[pdA-(p+\frac{\partial p}{\partial y}dy)dA+ρgdydA=0\]
となりますね。
これを式を整理すると、
\[\frac{\partial p}{\partial y}=-ρg\]
\(y\)方向もこのように求めることができます。
液面の形を求める

以上のように圧力は\(r\)と\(y\)の関数になっていることがわかりますね。
両方の方向に微小変化した時の変化量を考える必要が出てくるわけですが、これは数学的には全微分に相当します。
圧力の全微分は
\[dp=\frac{\partial p}{\partial r}dr+\frac{\partial p}{\partial y}dy\]
と書き表すことができますね。
偏微分の部分については先ほど計算したので、代入すると、
\[dp=ρrω^2dr-ρgdy\]
となります。
液面での圧力はゼロで一定となっているので、\(dp=0\)として、
\[ρrω^2dr=ρgdy\]
変形して、
\[\frac{dy}{dr}=\frac{rω^2}{g}\]
という微分方程式を得ることができます。
この微分方程式は簡単に解くことができて、両辺を\(r\)で不定積分して、
\[y=\frac{r^2ω^2}{2g}+C\]
\(r=0\)で\(y=0\)なので、積分定数\(C\)はゼロとなり、液面の形は
\[y=\frac{r^2ω^2}{2g}\]
と放物線になりますね。
まとめ

流体が回転している場合の相対的な静止状態を考え、液面の形状や圧力変化がどのようになっているかを解説しました。
遠心力という慣性力を考えることが大切なポイントになります。
計算するにあって全微分と偏微分が出てきて戸惑う方もいるかもしれませんが、しっかりと数学的な操作の意味も踏まえて理解していきましょう。
