断面2次モーメントと平行軸の定理がよくわからないんだけど…


断面2次モーメントは材料力学でも扱う内容だし、流体力学では少し取り扱い方に注意しないといけないから、しっかりと解説しておくね。
今回は断面2次モーメントと平行軸の定理について説明します。
いずれも流体力学だけでなく、力学全般を学ぶ上で大事な考え方ですので、しっかり学習していきましょう。
YouTubeでの動画はこちらです。
断面2次モーメント
前回、断面1次モーメントについて説明したのですが、
ポイント
- 断面1次モーメント 距離×微小面積
- 断面2次モーメント 距離の2乗×微小面積
という違いがあります。
2次モーメントなので距離の2乗になっている感じですね。
距離というものを考えないといけないので、必ずどこからの距離なのかを確認するようにしましょう。
点であったり、\(x\)軸や\(y\)軸といった軸からの距離を考えることが多いです。⚪︎⚪︎軸まわりのモーメント、と言ったりします。
力学でよくあるのは、図心の周りのモーメント、とかいう表現が多いですかね。
この断面2次モーメントは、材料力学だと、部材の構造的な曲がりにくさを表すのによく使いますね。
流体力学では断面2次モーメントは圧力中心を求めるのに使います。合わせて平行軸の定理もセットでよく出てきますので、後述しますね。
圧力中心との関係

さて、圧力中心を求めてみましょう。
その過程で断面2次モーメントが出てくるので、断面2次モーメントの必要性をそこで認識してもらえればと思います。
平板に発生した圧力を考え、その圧力によるモーメントを考えます。
\(x\)軸を液面、\(y\)軸をxに垂直にとり、\(x\)軸周りのモーメントを考えていきましょう。
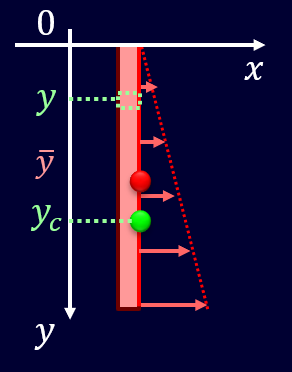
まず、圧力中心は全圧力\(F\)の作用点であるため、圧力中心のy座標を\(y_c\)とすると、平板にかかる\(x\)軸周りのモーメントは
\[y_c F\tag{1}\]
と書くことができますね。
一方、とある微小面積に発生するモーメントは、その\(y\)座標を\(y\)とすると、
\[ypdA\tag{2}\]
となりますので、平板にかかるモーメントはこの(2)を積分すればよく、
\[\int ypdA\tag{3}\]
となります。
圧力pは\(p=ρgy\)なので、
\[\int ρgy^2dA=ρg\int y^2dA\tag{4}\]
ここに断面2次モーメントが表れているのがわかりますでしょうか?
また、\(y_c F\)でモーメントは書き表すことができるのは先ほど説明した通りなので、
\[y_c F=ρg\int y^2dA\tag{5}\]
となり、圧力中心\(y_c\)は
\[y_c=\frac{ρg\int y^2dA}{F}\tag{6}\]
全圧力\(F\)は
\[F=\int pdA=ρg\int ydA\tag{7}\]
なので、
\[y_c=\frac{ρg\int y^2dA}{ρg\int ydA}\tag{8}\]
となります。
このように、圧力中心の位置には断面2次モーメントと断面1次モーメントが出てくるわけですね。
断面1次モーメントは前回の記事で解説しておりますので、そちらを参考にしていただければと思います。
問題はこの断面2次モーメントですね。
材料力学で習った方もいらっしゃるかもしれませんが、さらっと解説しようと思います。
断面2次モーメントとは
冒頭で述べたとおり、そもそもモーメントとは距離×⚪︎⚪︎という物理量です。
距離が1乗だと1次モーメント、2乗だと2次モーメントと呼ぶわけですね。
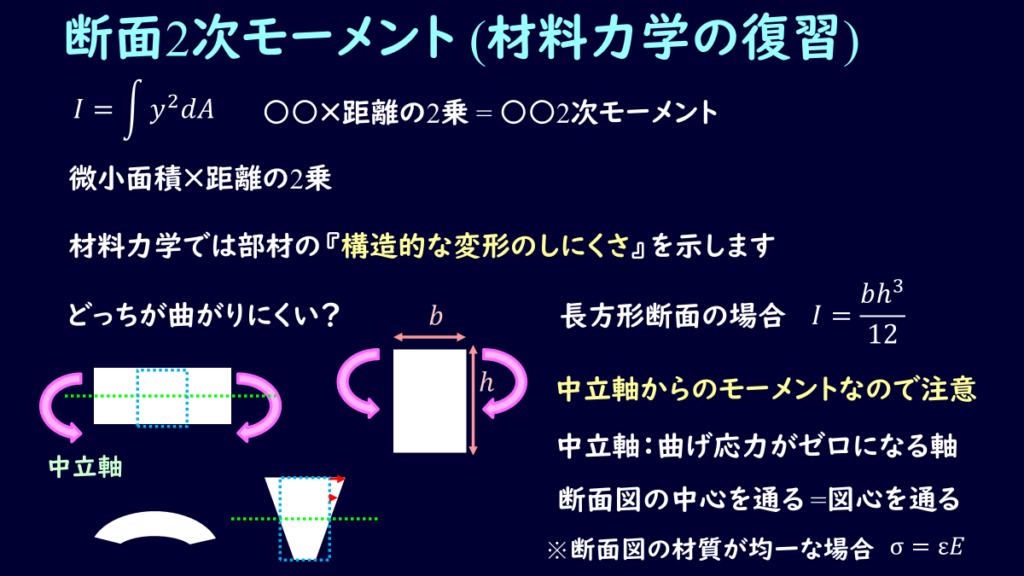
この断面2次モーメントは、材料力学では部材の構造的な曲がりにくさを示しています。
これ以上詳しくは材料力学の記事を参考にしていただきたいのですが、
大事なのは材料力学で考えている断面2次モーメントは中立軸周りのモーメントを考えている、ということです。
この中立軸は部材の材質(ヤング率)が均一であれば、図心を通る軸と一致します。
この図心を通る断面2次モーメントは、メジャーな断面形状であれば教科書などに乗っています。
が、流体力学の圧力中心で考えている断面2次モーメントは図心からではなく、今回の例だとx軸が水面の位置にあるので、水面からの断面2次モーメントです。
なのでパパッと計算することはできないので、平行軸の定理というものを使って計算します。
力学の慣性モーメントの分野で習った人もいるかと思いますが、一緒に復習しておきましょう。
平行軸の定理

それでは平行軸の定理について確認しておきましょう。
この平行軸の定理は、図心の位置からの断面2次モーメント\(\bar{I}\)がわかっていれば、それと平行な任意の軸からの断面2次モーメント\(I\)がわかるという優れものです。
式の形は
\[I=\bar{I}+Ad^2\tag{9}\]
と書くことができます。
断面積が\(A\)、求めたい軸と図心を通る軸の距離が\(d\)としています。
この式を使うと、圧力中心の式を変形することができ、
\[y_c=\frac{ρg\int y^2dA}{ρg\int ydA}=\frac{I+Ay^2}{Ay}\tag{10}\]
となります。
\(d\)は図心からの距離\(y\)に書き換えて、断面1次モーメントは前回の記事で説明した通り、\(Ay\)ですのでこのように変形できます。
さらに整理すると、
\[y_c=y+\frac{\bar{I}}{Ay}\tag{11}\]
と書くことができます。
この式は教科書とかでもよく出てくる式ですね。
まとめ
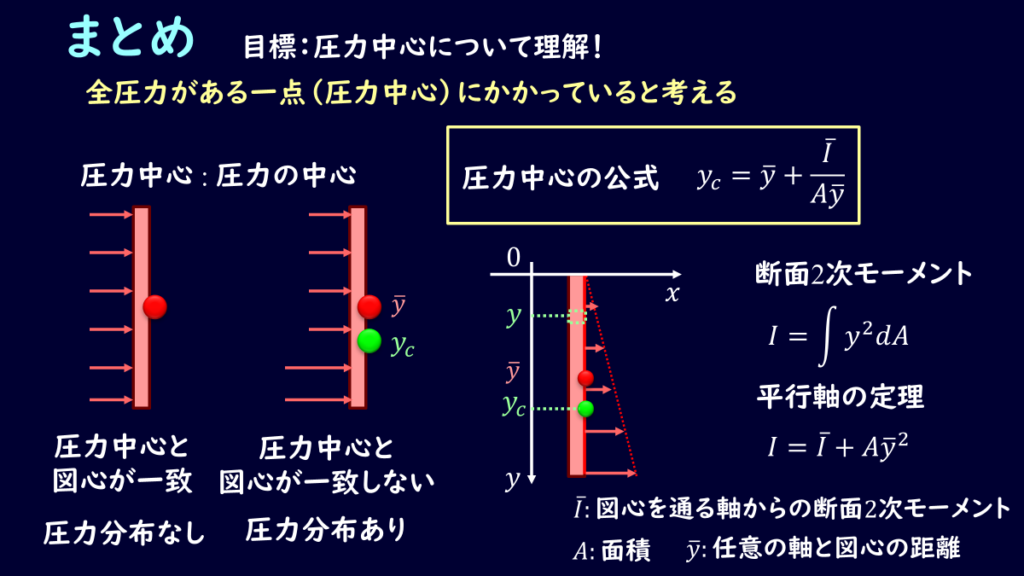
圧力中心について解説しました。
断面2次モーメントや平行軸の定理の理解ができていないと、式の意味がわからなくなりますし、使い方もわからなくなりますので、
しっかりと中身を理解しておきましょう。
