油圧ジャッキとか油圧シリンダーの問題が出てきてよくわからないんだけど…そもそも何に使うの?


パスカルの原理でよく使われる問題だね。油圧方式自体が結構便利なところもあるので、そのあたりも解説しておくね。
パスカルの原理の応用例として、油圧シリンダー、油圧ジャッキの練習問題を解きます。
結構、テストとかでも出たりするとは思いますが、色んなところに使われている便利な物たちだからなんですね。
今回はその辺りもしっかりと理解できるように説明していきます。
パスカルの原理そのものの説明については過去の講義で説明していますので、ぜひ参考にしていただければと思います。
また、動画でも解説していますので、そちらも参考にしていただければと思います。
なぜ油圧?

そもそもなぜ油なの?っていう疑問があると思いますが、上の図のようなことが挙げられますね。
油の特性
- 摩擦が少なく、エネルギーロスが少ない
- 水などより密度が高い
- 高温、低温で安定していて、温度変化に強い
- 金属が錆びなくて、装置が長持ち
油圧シリンダーだったり、油圧ジャッキというのは、力を増幅するような側面があるので、摩擦とかで力をロスしたくないわけですね。
なのでツルツル滑る油のほうが水などより適しているということになります。
また、密度が高いということで、力を伝えやすくなります。
スカスカのものを使うよりぎっしり詰まった方が力が分散しにくそうなイメージは沸きますよね?
ただ、サラダドレッシングとかの油は、水より密度が低いので、油によっては密度が低いものもあることを認識しておきましょう。
油圧系の装置とかで使う作動油などは密度が高くなっている、ということですね。
次に油は高温、低温で安定しているというのは、広い温度帯で液体のままいてくれる、ということを指します。
水なら氷点下で氷に、100℃を超えると水蒸気になりますね。こうなると液体をベースに設計された装置では使えなくなってしまいます。
ロシアとか北海道とか寒いところだと水が凍って使えなくなるわけです。
その点、油は液体のまま存在できる温度帯が水より広いので、寒い地域でも暑い地域でも使用できるということになります。
最後に金属が錆びないというのも利点です。
水に金属をつけておくと錆びてしまいますが、油なら大丈夫。錆止めとしての油もあったりしますね。
油圧シリンダー
それでは油圧シリンダーについてです。
そもそもどういう構造のものかを示しておきますね。
高校物理の熱力学とかでもよく出てきたピストンみたいなもんです。
アクチュエーターとして産業的には使われたりします。
油流してピストン動かす、みたいな感じ。
さて、前置きが長くなりましたが、油圧シリンダーの問題を考えていきましょう。
いろんな形のものがありますが、上図のような単純なものを考えます。
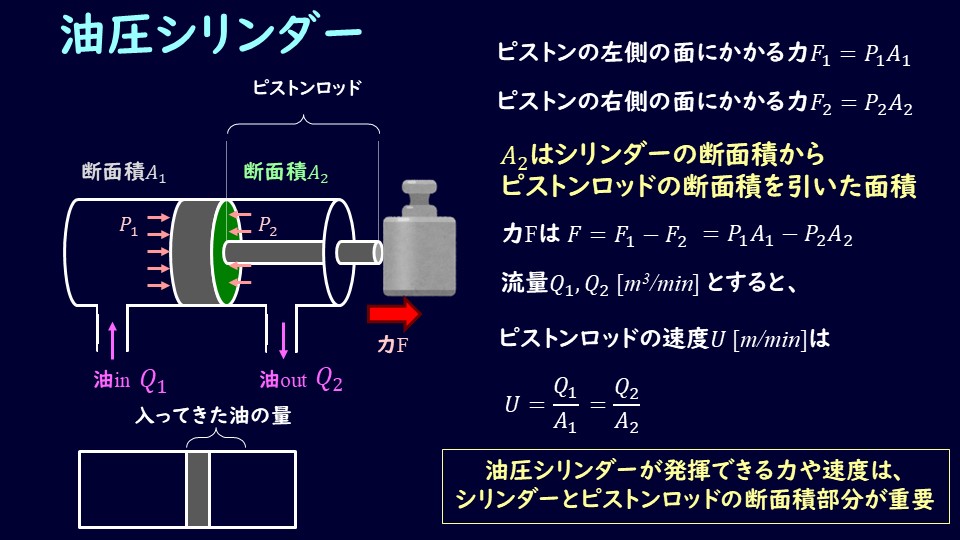
このシリンダーは油を流すことでピストンが動き、ピストンロッドによってモノを動かす形になります。
このピストンロッドの力と速度を計算してみましょう。
ピストンの左側の圧力を受ける面積を\(A_1\)、右側の圧力を受ける面積を\(A_2\)としています。
ピストン右側にはロッドがついているので、ロッドの分だけ、圧力を受ける面積が小さくなりますね。
さて、次に圧力を考え、トータルの力がどうなるかを考えましょう。
ピストンの左側の面にかかる圧力を\(P_1\)、ピストンの右側の面にかかる圧力を\(P_2\)とすると、左右の面それぞれにかかる力は、
左側の面 \(F_1=P_1A_1\)
右側の面 \(F_2=P_2A_2\)
となります。
ピストンロッドの力\(F\)はこれらの差分になるので、
\[F=F_1-F_2=P_1A_1-P_2A_2\tag{1}\]
と書くことができます。
いや、これだけやったら普通に押したらいいやん!ピストンとか邪魔やん!


まぁピストンを手で動かすのならそうだね。でも、油を使って動かすことができるっていうのがポイントなんだよ。
油というものを経由して動かすことで、力の向きを変えたり、電動ポンプなどの機器を使って大きな力を扱えるようになったりします。
というわけで油を流すことを考えましょう。
また、前提知識として流量について説明しておきます。
これは油圧シリンダーに油を流し込むことで、ピストンが動くわけですが、その油を流し込んだ量を定義づけしておく必要があります。
流入量と流出量をそれぞれ\(Q_1、Q_2\)とします。単位は\(m^3/min\)です。
1分間でどれくらいの体積の油が出て行ったり入ったりしたか、を示しています。
ピストンロッドが入ってきた油によって1分間で動く量は
\[Q_1/A_1\]
となります。
流出量の方も同様で、
\[Q_2/A_2\]
だけ動くことになりますね。
ピストンロッドの速度を求めるには流入量、流出量のどちらかを使えば求まりますが、
今回は流入量がわかっているとして、ピストンロッドの速度を求めようと思います。
ピストンロッドの速度をUとすると、
\[U=Q_1/A_1\tag{2}\]
となりますね。
ちなみに流出量を使うと
\[U=Q_2/A_2\tag{3}\]
となりますので、上の流入量の式と繋ぐことで
\[Q_2=Q_1A_2/A_1\tag{4}\]
と流出量も求めることができます。
さて、ここまでの導出で、勘が良い方は気づいたかと思いますが、
油圧シリンダーの性能を決めているのは、ピストンの受圧面積とピストンロッドの断面積となります。
これは油圧シリンダーが発揮できる力の式にも、速度の式にも受圧面積が含まれているからですね。
油圧ジャッキ
パスカルの原理といえば油圧ジャッキと言われるくらい、流体力学の教科書にはほぼ確実に載っているのではないでしょうか?
少ない力で重たいものを持ち上げるものですね。
車とかも持ち上げることができます。
力の増幅装置、と呼ぶと魔法のように感じますが、ちゃんとエネルギーは保存しています。
さて、それでは油圧ジャッキの問題を解いていきましょう。
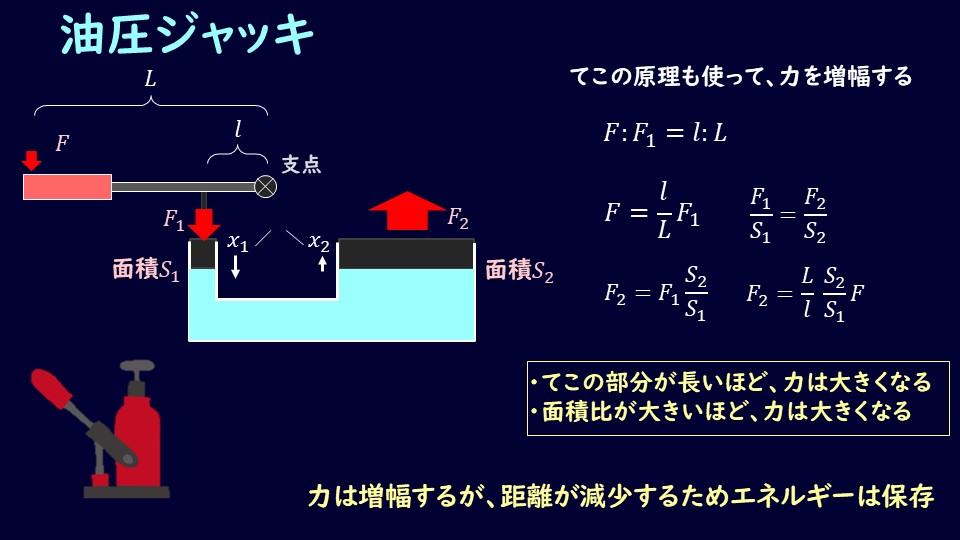
上図のような感じでレバーがついた油圧ジャッキがよく扱われるのでこれを題材にしていきます。
さて解いていきましょう。
まずテコにかける力を\(F\)とすると、油圧ジャッキの部分にかかる力\(F_1\)はテコの原理で増幅されますね。
図のように持ち手から支点までの距離をL、支点から油圧ジャッキまでの距離をlとしますと、\(F_1\)の大きさはテコの原理より、
\[F:F_1=l:L\]
となり、
\[F=l/LF_1\tag{5}\]
と表すことができます。
次にパスカルの原理から\(F_1\)とジャッキが発揮できる力\(F_2\)の関係を見てみると、
\[\frac{F_1}{S_1}=\frac{F_2}{S_2}\tag{6}\]
となりますね。この式から\(F_2\)を求めると、
\[F_2=F_1\frac{S_2}{S_1}\tag{7}\]
となります。\(F_1\)はてこの原理から、\(F\)の式で表すことができるので、
\[F_2=\frac{L}{l}\frac{S_2}{S_1}F\tag{8}\]
となって、油圧ジャッキによる力が求まります。
問題によっては具体的な力を求めるように問題文に数値が設定されていたりしますが、その場合は上で求めた式に数値を入れていけば求まりますので、ぜひ一度は自分の手で計算してみることをお勧めします。
まとめ
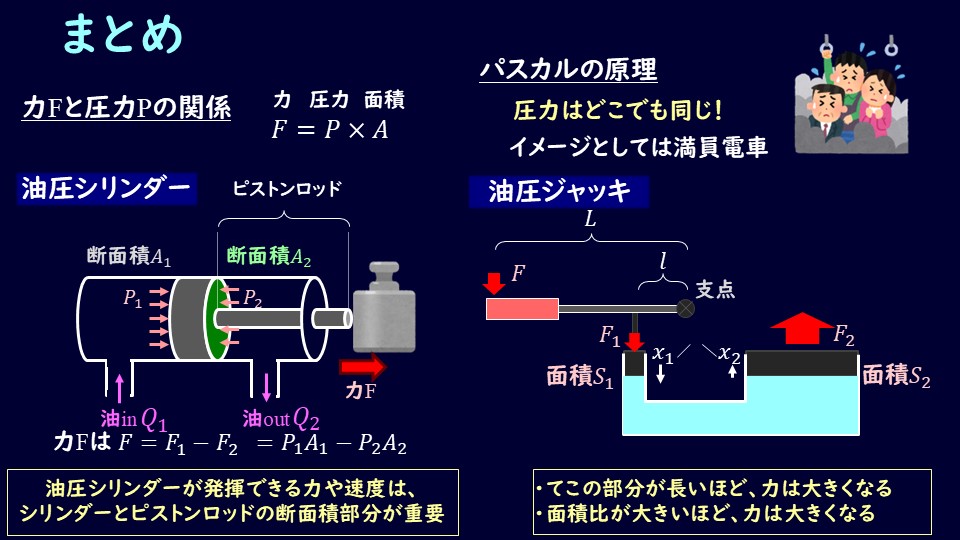
パスカルの原理の例題として、油圧シリンダーと油圧ジャッキを解説しました。
どちらも基礎的な内容ですので、しっかりと理解しておきましょう。
