上の板が動いている場合の粘性流体って流速分布どうなるの?


考え方はポアズイユ流れとよく似た形になるよ。境界条件に注意だね。
今回は隙間に流体を流して、なおかつ上の板が動くときの流体の挙動を考えましょう。
この問題は軸受などの工業的にも重要な部品に使われる物理の基礎となります。
問題設定
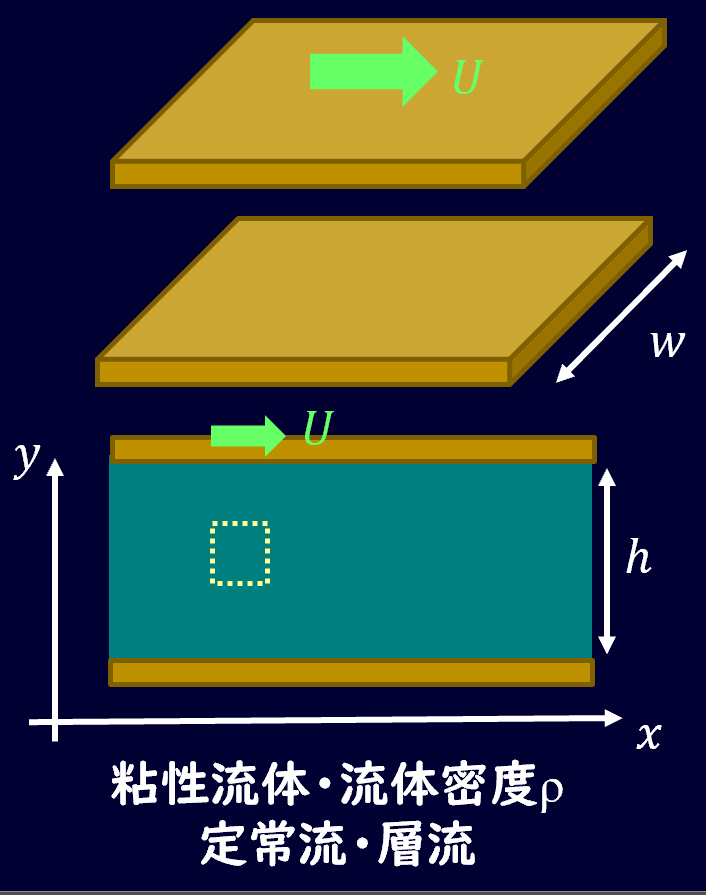
平行平板を考え、座標軸を図のように取り、平板の上側が速度\(U\)で動くとします。
平板間の距離を\(h\)とします。
流体は粘性流体で層流の状態で、定常流で流れているとします。
板の速度を求める
前回の記事までの考え方を踏まえて、板の速度を求めましょう。
板の速度を求めるには上板と接している流体の流速が\(U\)となっているとすれば、流速を求めることで板の速度を求めることができますね。
また、定常流となっていることから、流速は時間変化していませんので、流体素片に対して力のつり合いを考えればよいことがわかります。
力のつり合いの式には、粘性流体を考えている以上、せん断力の項が存在してくるはずなので、そのせん断力に対してニュートンの粘性法則を適応させると流速が求まりますね。
ということで、まずは力のつり合いの式を考えましょう。
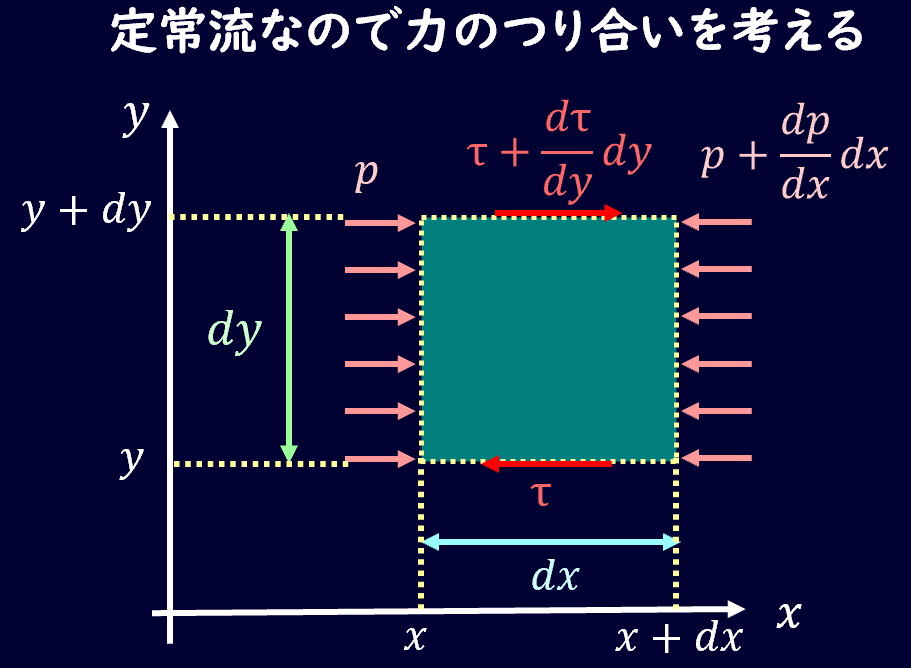
左側の面にかかっている圧力を\(p\)、粘性によって発生しているせん断力をτとすると、
\[pdy-\left(p+\frac{\partial p}{\partial x}dx\right)dy-τdy+\left(τ+\frac{\partial τ}{\partial y}dx\right)dy=0\]
となります。
式を整理すると微分形の部分だけが残るので、
\[\frac{\partial p}{\partial x}=\frac{\partial τ}{\partial y}\]
と簡単な形になります。
ここで、ニュートンの粘性の法則から
\[τ=μ\frac{dv}{dy}\]
なので、これを代入すると、
\[\frac{\partial p}{\partial x}=μ\frac{\partial^2 v}{\partial y^2}\]
となりますね。あとは両辺を\(y\)で2回積分することで、\(v\)の式が出てきますので、積分してやると、
\[v=\frac{1}{2μ}\frac{\partial p}{\partial x}y^2+C_1y+C_2\]
積分定数を\(C_1、C_2\)としています。
ここまでは前回と同じ内容ですね。
異なってくるのはここからで、境界条件が少し異なってきます。
\(y=0\)の点で\(v=0\)となるのは前回と同じですが、\(y=h\)で\(v=U\)となるのですね。
まず、\(y=0\)の条件から
\[C_2=0\]
次に\(y=h\)の条件から
\[U=\frac{1}{2μ}\frac{\partial p}{\partial x}h^2+C_1h\]
ここから\(C_1\)を求めると、
\[C_1=\frac{U}{h}-\frac{1}{2μ}\frac{\partial p}{\partial x}h\]
となり、
\[v=\frac{1}{2μ}\frac{\partial p}{\partial x}y^2+\left(\frac{U}{h}-\frac{1}{2μ}\frac{\partial p}{\partial x}h\right)y\]
少し整理して
\[v=-\frac{1}{2μ}\frac{\partial p}{\partial x}y(h-y)+\frac{U}{h}y\]
となります。
この式の第1項は前回取り扱ったポアズイユ流れの流速の式、第2項は前々回のクエット流れの式ですね。
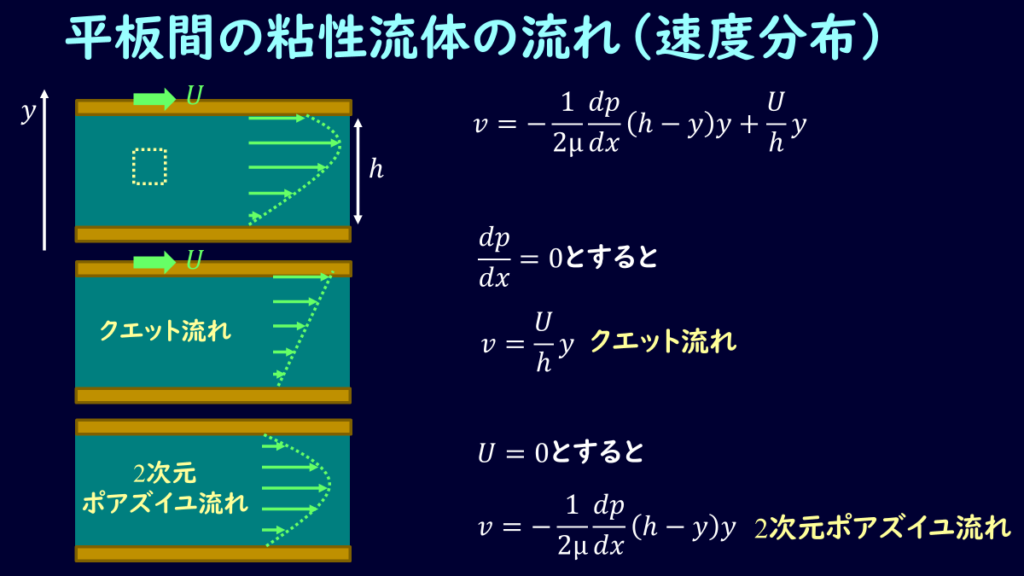
第2項を残すためには、第1項をゼロにすれば良く、1番よく使われる例としては圧力勾配の部分をゼロにする例ですね。
圧力勾配がゼロのような流れのときには、クエット流れのような状態になります。
逆に板を動かさず、\(U=0\)とすると、第2項が消去され、前回取り扱ったポアズイユ流れになりますね。
流量を求める

さて、それでは流量を求めてみましょう。
求め方は前回と同じで、流速が\(y\)軸方向で分布があるため、積分して求めることになります。
単位幅の流量を\(Q\)とすると、
\[Q=\int^h_0vdy=\int^h_0\left(-\frac{1}{2μ}\frac{\partial p}{\partial x}y(h-y)+\frac{U}{h}y\right)dy\]
この積分を計算すると、
\[Q=-\frac{1}{12μ}\frac{\partial p}{\partial x}h^3+\frac{U}{2}h\]
と求まります。
まとめ
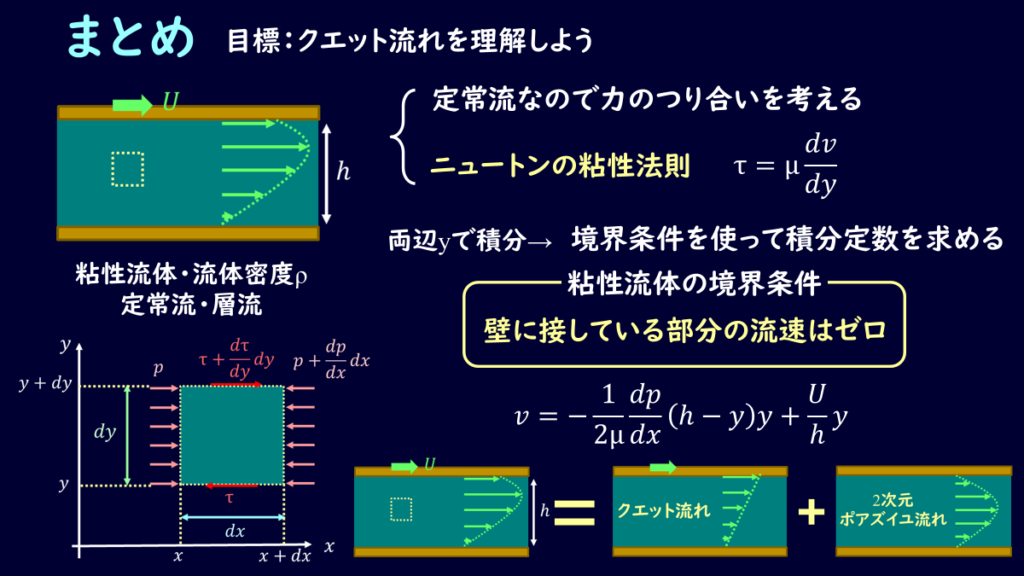
上板が動く場合の粘性流体の流れを解説しました。
圧力勾配の有無によってポアズイユ流れの成分がなくなり、クエット流れになることもありますので注意しましょう。
