何このぽあずいゆ流れって…よくわからないし、舌噛みそうなんやけど…


粘性流体の流れ方ですごく基本的な流れ方なので、解説するね。
今回はポアズイユ流れについてです。
非常によく出てくる流れ方なので、しっかりと理解しておきましょう。
粘性流体を流したときの流速
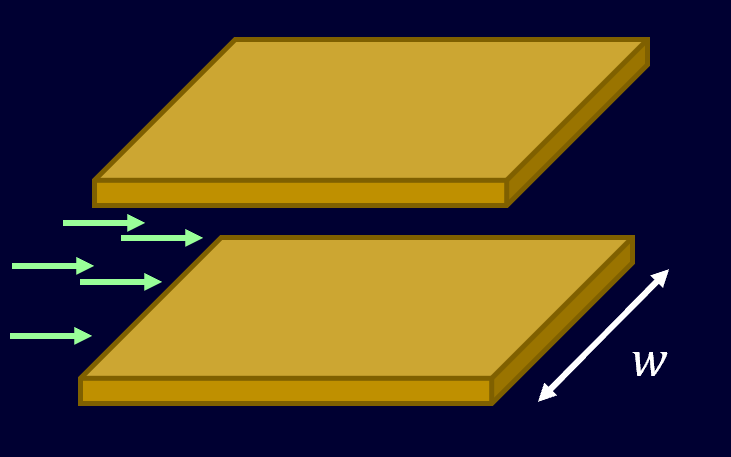
上図のように、板の間を流体が流れるとします。
板は固定されており、流体は粘性流体として扱い、定常流になっているとします。
この時、板の間の流速分布はどのようになるか考えましょう。
図のように座標軸を取ります。
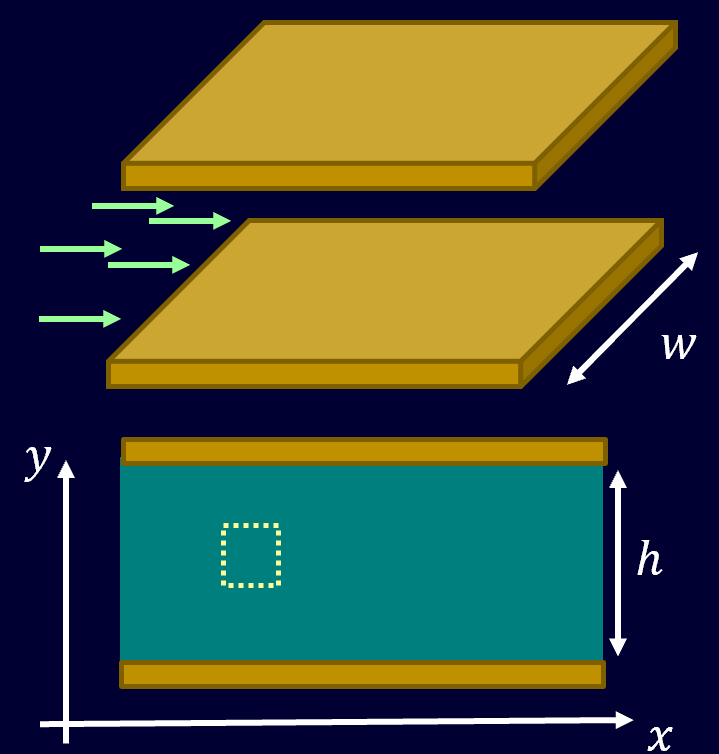
定常流になっているので、とある部分の流体素片には力のつり合いが成立していることになります。
板に垂直な面を2つ、距離\(h\)で配置されているとします。
この2つの面に囲われている流体の中の微小部分を考えると、力のつり合いが成立しますので、左側の面にかかっている圧力を\(p\)、粘性によって発生しているせん断力をτとすると、
\[pdy-\left(p+\frac{\partial p}{\partial x}dx\right)dy-τdy+\left(τ+\frac{\partial τ}{\partial y}dy\right)dx=0\]
と書き表わすことができます。
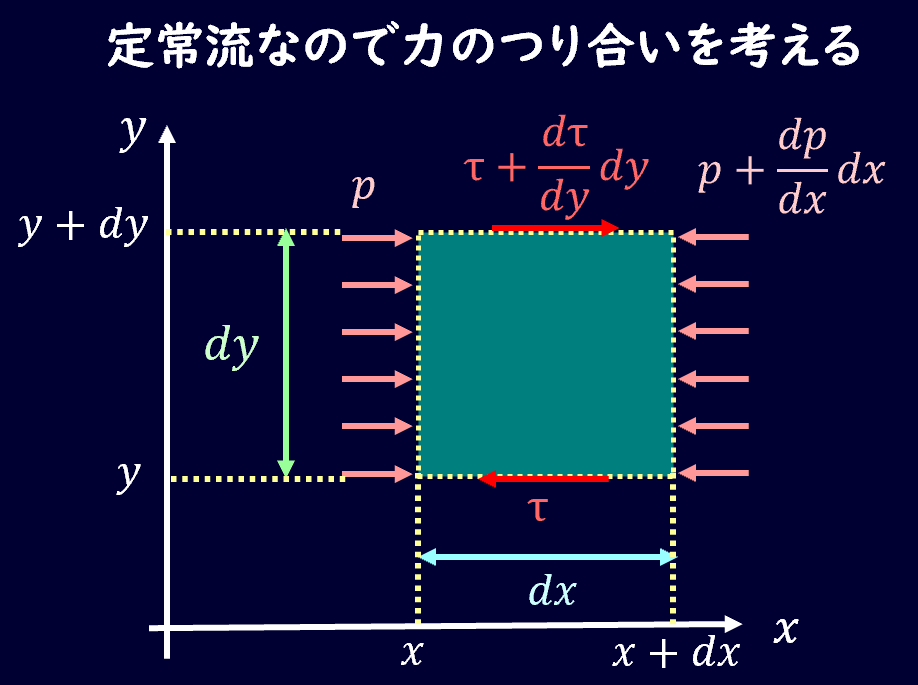
式を整理すると微分形の部分だけが残るので、
\[\frac{\partial p}{\partial x}=\frac{\partial τ}{\partial y}\]
と簡単な形になります。
ここで、ニュートンの粘性の法則から
\[τ=μ\frac{dv}{dy}\]
るとなりますが、流速\(v\)は\(y\)のみの関数として、偏微分に置き換えます。
これを代入すると、
\[\frac{\partial p}{\partial x}=μ\frac{\partial^2 v}{\partial y^2}\]
となりますね。あとは両辺を\(y\)で2回積分することで、\(v\)の式が出てきますので、積分してやると、
\[v=\frac{1}{2μ}\frac{\partial p}{\partial x}y^2+C_1y+C_2\]
となります。
今、粘性流体を考えているので、\(y=0\)と\(y=h\)で流速\(v=0\)となり、これらを代入して積分定数を求めましょう。
\(y=0\)の条件から
\[C_2=0\]
となり、次に\(y=h\)の条件から
\[\frac{1}{2μ}\frac{\partial p}{\partial x}h^2+C_1h=0\]
これを解くと
\[C_1=-\frac{1}{2μ}\frac{\partial p}{\partial x}h\]
となります。
以上より、流速の式は
\[v=\frac{1}{2μ}\frac{\partial p}{\partial x}(y-h)y\]
と\(y\)の二次関数として書けるわけですね。
このような流速が2次元断面で、二次関数的に変化する流れを2次元ポアズイユ流れと呼んでいます。
流量と圧力を考える
流速が\(y\)方向で変化しているため、流量\(Q\)を考える際には微小面積を考えて積分する必要があります。
単位幅の流量を\(Q_w\)とすると、
\[Q_b=\int^h_0 vdy=\left[\frac{1}{2μ}\frac{\partial p}{\partial x}(\frac{1}{3}y^3-\frac{1}{2}hy^2)\right]^h_0\\=-\frac{1}{12μ}\frac{\partial p}{\partial x}h^3\]
と計算できますね。
あれ?マイナスついてるけど大丈夫?


\(p\)の偏微分のところが基本的にはマイナスになるので大丈夫だよ。
ここで圧力が板に沿って直線的に減少するとします。
板の長さ\(l\)だけ進んだところで\(Δp\)の圧力変化が起こるとすると、
\[\frac{\partial p}{\partial x}=-\frac{Δp}{l}\]
と書き表わすことができます。
よって流量は、板の幅を\(w\)とすると、
\[Q=wQ_w=\frac{w}{12μ}\frac{Δp}{l}h^3\]
となり、板の隙間\(h\)の3乗、板の幅の1乗に比例し、板の長さ\(l\)に反比例します。
円環状の流体の流れ
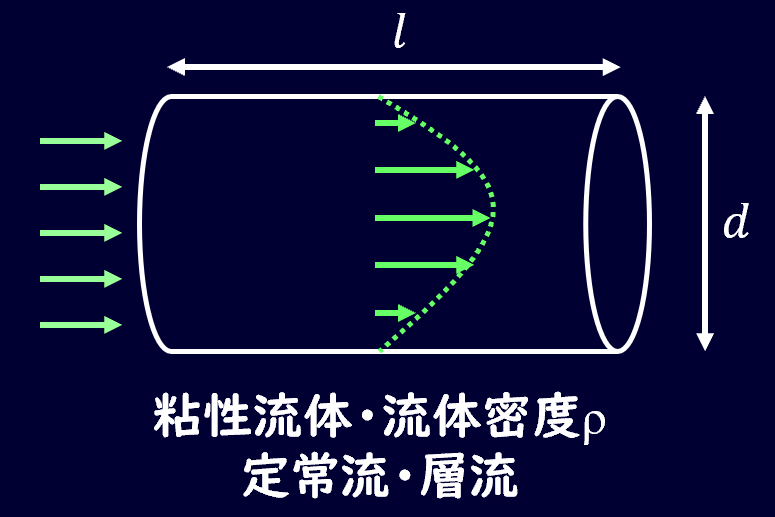
これまで板の間の流れを考えていましたが、円環状の管を流れる粘性流体について考えてみましょう。
よくあるストローの例です。
前提として、粘度μの粘性流体が中心軸に対称に流れており、定常流であるとします。

定常流であるため、力のつり合いを考えればよく、図の枠部の流体にかかっている力を考えると、圧力を\(p\)、壁から受けるせん断力をτ、流体素片の断面積の半径を\(r\)とすると、
\[πr^2p-\left(\frac{\partial p}{\partial x}dx\right)πr^2-2πrdxτ=0\]
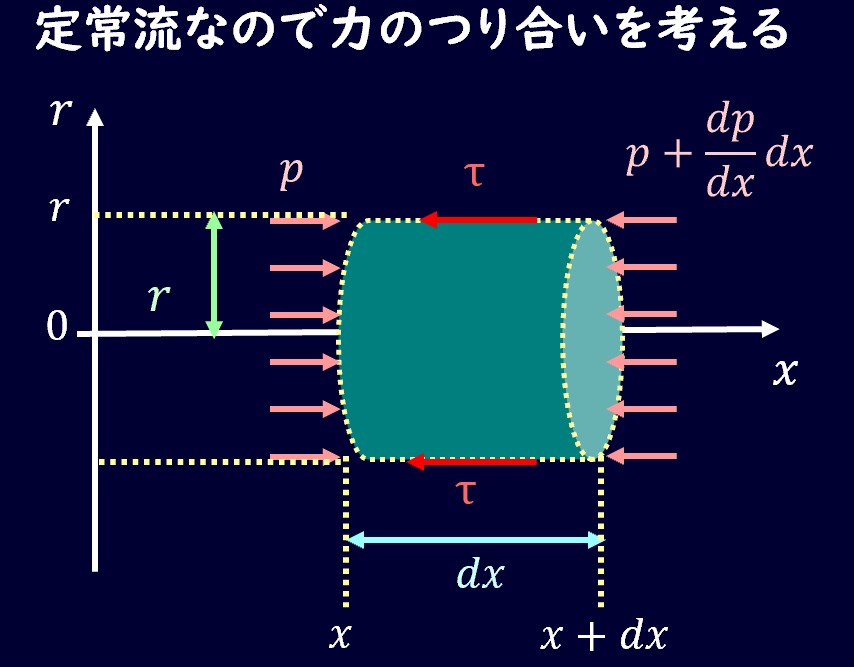
この式を整理すると、せん断力τは、
\[τ=-\frac{r}{2}\left(\frac{\partial p}{\partial x}dx\right)\]
またニュートンの粘性法則より、
\[τ=-μ\frac{dv}{dr}\]
であるので、
\[τ=-μ\frac{dv}{dr}=-\frac{r}{2}\left(\frac{\partial p}{\partial x}\right)\]
となり、
\[μ\frac{dv}{dr}=\frac{r}{2}\left(\frac{\partial p}{\partial x}\right)\]
と整理することができます。
あとは両辺を\(r\)で積分すると、流速\(v\)の式が出てきますので、不定積分してやると、
\[v=\frac{r^2}{4μ}\left(\frac{\partial p}{\partial x}\right)+C\]
境界条件\(r=r_0\)で流速はゼロになるので、積分定数\(C\)は
\[C=-\frac{r_0^2}{4μ}\left(\frac{\partial p}{\partial x}\right)\]
となり、
\[v=-\frac{r_0^2-r^2}{4μ}\left(\frac{\partial p}{\partial x}\right)\]
と求めることができます。
この式を見てみると、流速が放物線を中心軸でぐるっと回転させたような形状分布になっていることがわかりますね。
流量を求める
さて、次に流量を求めにいきましょう。
先ほどの固定板の間の流体の時と同じように、微小領域を設定して、積分することで求めることができます。
微小領域を円環状態に取り、半径\(r\)の関数になるように設定します。
微小な円環の面積を\(dA\)とすると、
\[dA=2πrdr\]
なので、微小な円環を流れる流量\(dQ\)は
\[dQ=dAv=2πrdr×v\]
これを\(r=0\)から\(r=r_0\)まで積分すればよく、
\[Q=\int^{r_0}_02πrvdr=-\frac{2π}{4μ}\left(\frac{\partial p}{\partial x}dx\right)\int^{r_0}_0(r_0^2-r^2)rdr\]
この積分を計算すると、
\[Q=-\frac{π}{8μ}\frac{\partial p}{\partial x}r_0^4\]
この式からわかるように、流量は管の内径の4乗に比例することになります。
半径ではなく直径\(d\)で表すことが多いので、直径を使って表すと、
\[Q=-\frac{π}{128μ}\frac{\partial p}{\partial x}d^4\]
また、圧力変化の部分について、長さ\(l\)で\(Δp\)変化するとして、線形的に変化するとしたとき、固定板の間を流れる流体の時と同様に、
\[-\frac{\partial p}{\partial x}=\frac{Δp}{l}\]
となるので
\[Q=-\frac{Δpπ}{128μl}\frac{\partial p}{\partial x}d^4\]
という形に変形できます。
この式をハーゲン・ポアズイユ流れと呼び、円形の断面を持つ流管の流量を表す式となっています。
まとめ
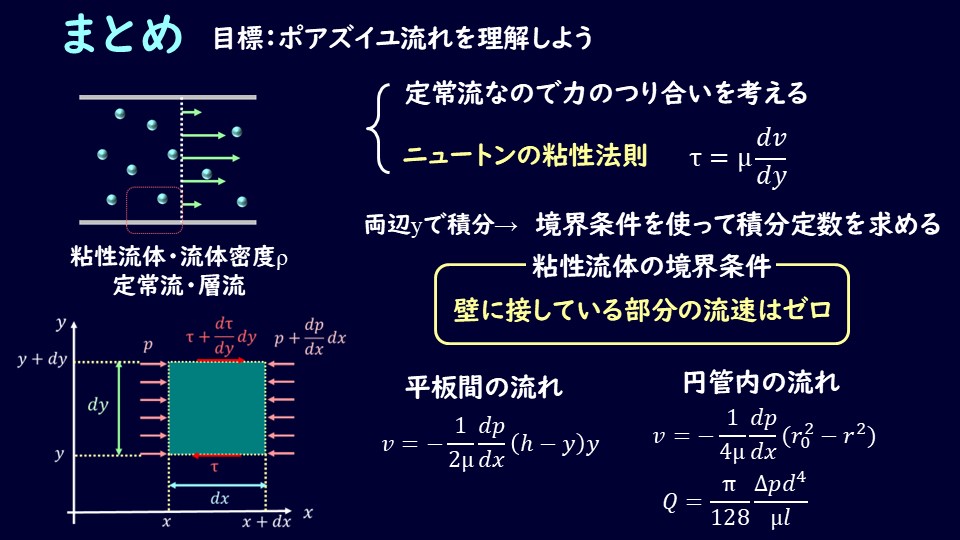
円管路の流体の流れであるポアズイユ流れについて説明しました。
現象的には流速が二次関数的に変化することを認識しておき、流量の式がどういう形で表されるかをしっかりと把握しておきましょう。
